MCMC：Markov Chain&Monte Carlo（二）MH采样和Gibbs采样，MCMC局限性
MCMC全称是Markov Chain & Monte Carlo。
在概率图的框架中属于近似推断中的不确定性推断，与之相对的有近似推断中的变分推断(variational Inference)。
MCMC本质是基于“采样”的“随机”“近似”。有三个关键词。
①采样是说MCMC本质就是一种引入Markov Chain模型实现采样任务的一种方法，本质是一种采样方法（Method）。
②随机是说MCMC的主要实现方法是找到一个随机矩阵(stochastic matrix)，也就是状态转移矩阵(也可以是状态转移概率密度函数)，使得
该Markov Chain最终达到一个平稳分布q(x)。
t=1到t=2相邻状态的随机矩阵
③近似是说q(x)与目标概率p(x)非常接近。
所以这里引入几个概念：分别是平稳分布，细致平衡（Detailed Balance）,燃烧期（burn-in），混合时间（mixing time）。
①平稳分布指的是每个时刻的状态变量X都满足一个概率分布p(X)，比如X1~p1(X),X2~p2(X),X3~p3(X)...XN~pN(X)，如果p1(X)=p2(X)=p3(X)=...=pN(X)=p(X)，则称p(X)为该Markov Chain的一个平稳分布。
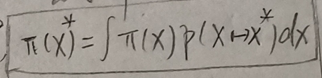
平稳分布的表达式
其中X是t时刻的随机变量，X*是t+1时刻的随机变量，p(X)是X服从的概率分布，p(X*)是X*服从的概率分布。p(X→X*) <=> p(X*|X)，相当于一个条件概率，代表given X，X*的概率分布。
②细致平衡是平稳分布的充分不必要条件，由细致平衡可以推出平稳分布。
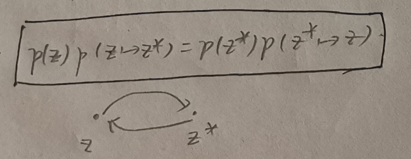
细致平衡简单示意
其中z是t时刻的随机变量，z*是t+1时刻的随机变量，p(z)是z服从的概率分布，p(z*)是z*服从的概率分布。p(z→z*) <=> p(z*|z)，相当于一个条件概率，代表given z，z*的概率分布。（和上文的X是一个含义，只不过用了不同的符号，凑合看吧...）。
③燃烧期和混合时间：若一个Markov Chain经过t=1~m时间段的状态变换，在t=m+1时刻往后的随机变量就收敛到平稳分布，那么将t=[1,m]称为燃烧器，m称为mixing time。
MCMC方法相关概念简单小结：
MH采样方法：
由于一个普通的Markov Chain每个时刻对应的随机变量Xt和每组相邻时刻间的{Pt,t+1}是不一样的，所以需要引入一个接受率α，使得每组相邻时刻的概率分布和随机矩阵满足Detail Balance条件，α的公式如下：
最终得到MH算法流程如下：
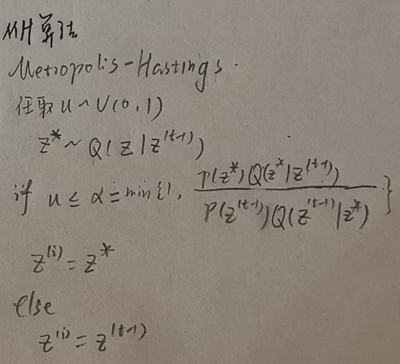
MH算法引出小结：
MH采样全称是Metropolis Hastings，MH算法的主要思想是引入接受率α=min{1,p(x*)Q(x|x*)/(p(x)Q(x*|x)}，使得相邻时刻间的状态转移矩阵Q(x,x*)和原始概率分布p(x),p(x*)满足Detail Balance条件，从而在经过mixing time长度的时间过后，得到平稳分布q(x)，其中q(x)与原始概率分布p(x)很相近，然后通过Markov Chain若干个时刻的状态变量值Xm，Xm+99，...等等得到基于MCMC方法的采样值。
Gibbs采样方法：
Gibbs采样是接受率α=1的MH采样，可以看作MH采样的特殊形式。适用于随机变量X维度非常高的情况，从t到t+1时刻，只改变一个维度的值。状态转移矩阵取得就是目标概率p(X)。
由于接受率α=1，所以采样效率高。
MCMC局限性
要了解MCMC的局限性，首先要了解为什么要采样，什么是好的采样，以及采样为什么困难。
①为什么要采样：
(i)一种情况是给定一些样本{Xi},i=1:N，这些样本满足一定的概率分布p(X)，现在要求增加样本数量，这个时候就需要对p(X)进行采样。
(ii)另一中情况是求解的问题的变量X是随机变量，问题可以抽象为f(X)，因为X是随机变量，所以需要对X服从的概率分布求期望，即求解Ep(X)[f(X)]。
②好的采样
需要满足X(1),X(2),...,X(i)等采样点相互独立。
③采样为什么困难
由于随机变量X维度太高，导致p(X)太复杂，所以无法求出p(x)对应的cdf，就没有办法通过cdf基本采样方法进行采样。由于X维度很高，导致很难知道p(X)长什么样子，也就很难找到一个跟它很像的proposal distribution q(X)，然后通过或者 Importance Sampling的方法进行采样。所以会提出MCMC的方法。
④MCMC的局限性：
1）采样点之间不独立（硬伤），解决方法，比如隔N个点采一个X(i)。
2）mixing time可能会很长，(单峰vs 多峰)，即模型可能就在初始状态在的某个分布内来回打转，由于两个分布的峰谷太低，采样点到达峰谷的概率非常低（特别是X是高维随机变量的情况下），这就导致MCMC没法采样到能够很好地表征p(X)概率分布的采样点，也就是mixing time会无限长，造成采样失败的情况。
3）就算采样成功了，也不能够确切的知道什么时刻已经达到了平稳分布，只能通过每隔一段时间就针对当前时刻的分布Xt采用，得到其采样的概率分布q1(X)，与目标概率分布p(X)对比，确定两者相似程度，从而判断是否达到平稳分布。
参考资料：
1.https://www.bilibili.com/video/BV1dW411z7qs?p=8，B站up主，作者shuhuai008。
