指数族分布：相关概念理解

一、指数族分布指的是概率密度函数都能够表述成以下形式的概率分布。

 其中fai(x)是充分统计量，A(ita)是对数配分函数。ita是规范化参数。【配分函数其实就是归一化因子的概念，为了使概率满足概率总和为1的约束】

指数族分布包括Gauss分布，bernoulli分布（0，1分布）,beta分布，gamma分布，二项分布（多项式分布），Dirichlet分布等。这些分布的概率密度函数都可以表示成上图中式子的形式。

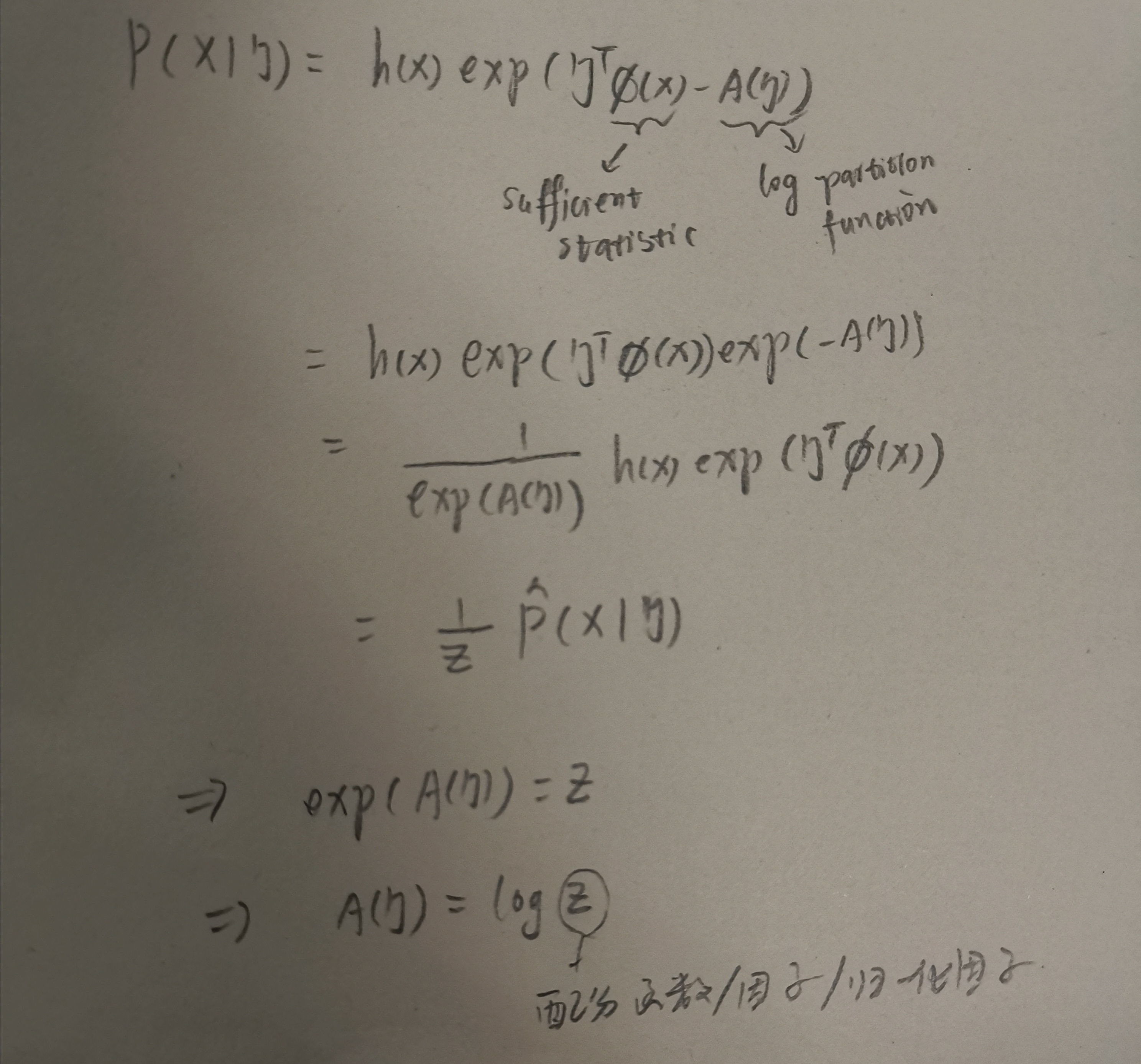
　　　　　　　　　　　　对数配分函数的推导

举例将高斯分布的概率密度函数用指数族分布的形式表达如下：

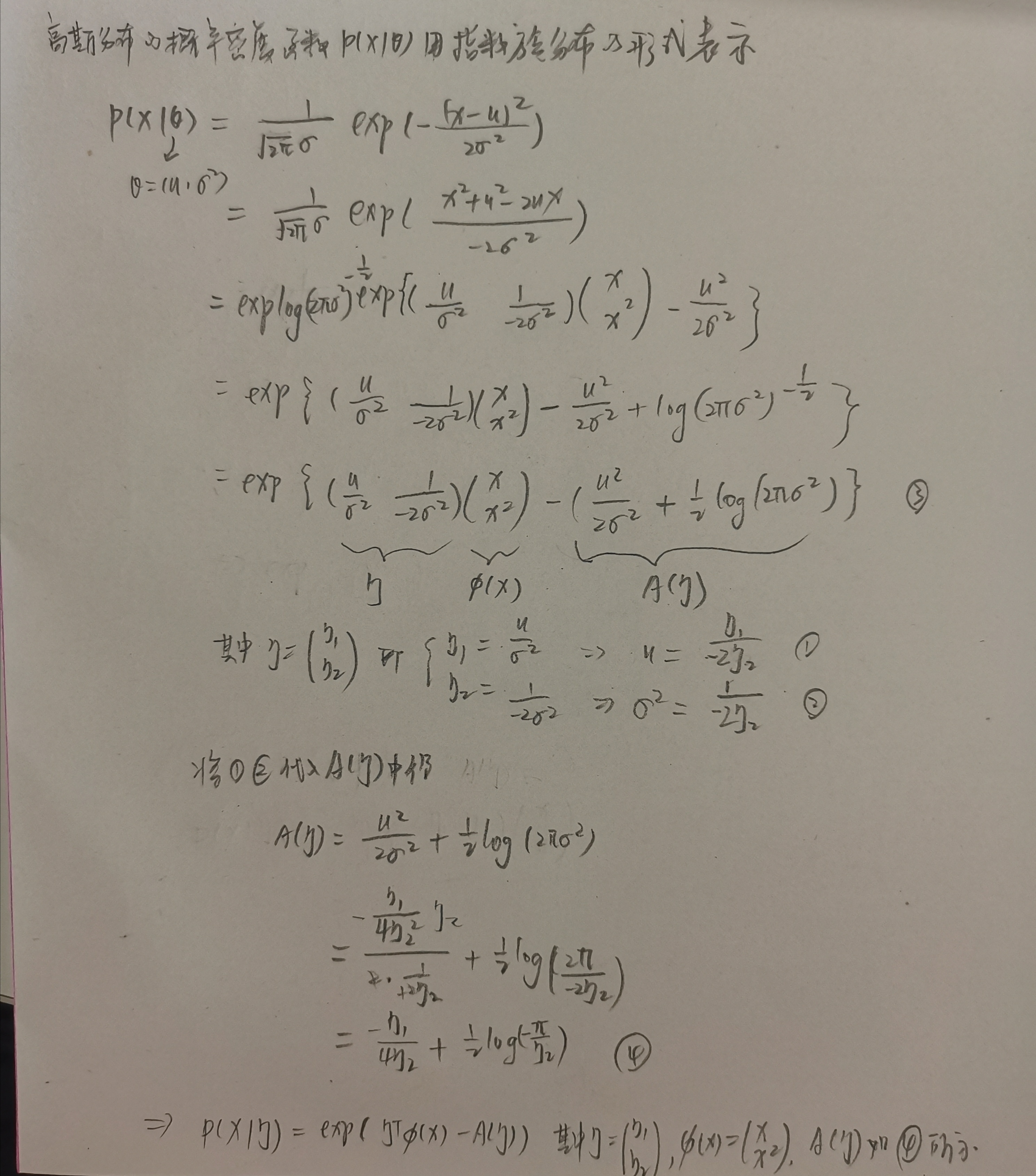
三、指数族分布有三个重要性质，分别是充分统计量、共轭、最大熵。

①关于充分统计量：（sufficient statistic）的理解：比如高斯分布中的{均值、方差}就是一组充分统计量，通过{均值，方差}我们就能得到这一组数据的大部分信息。（待确定）

不仅是{均值，方差}，也可以是{sum(xi),sum(xi)^2}...，【查找相关统计概念】

充分统计量“充分”指的就是参数组{ ..}包含的原始数据的信息足够多，可以用于压缩数据。

“统计量”指的就是数学意义上一组数据的统计量，比如均值，方差...。

 ②关于共轭：是通过似然和先验的共轭关系，将先验的分布与后验的分布联系起来。如果似然和先验共轭，那么后验的分布与先验的分布是同一种分布。

 ③关于最大熵：【待定：对未知参数的估计，往最随机的方向假定。】

 

四、指数族分布中A(ita)和fai(x)的关系、A'(ita)和fai(x)的关系

①：A'(ita)和fai(x)的关系

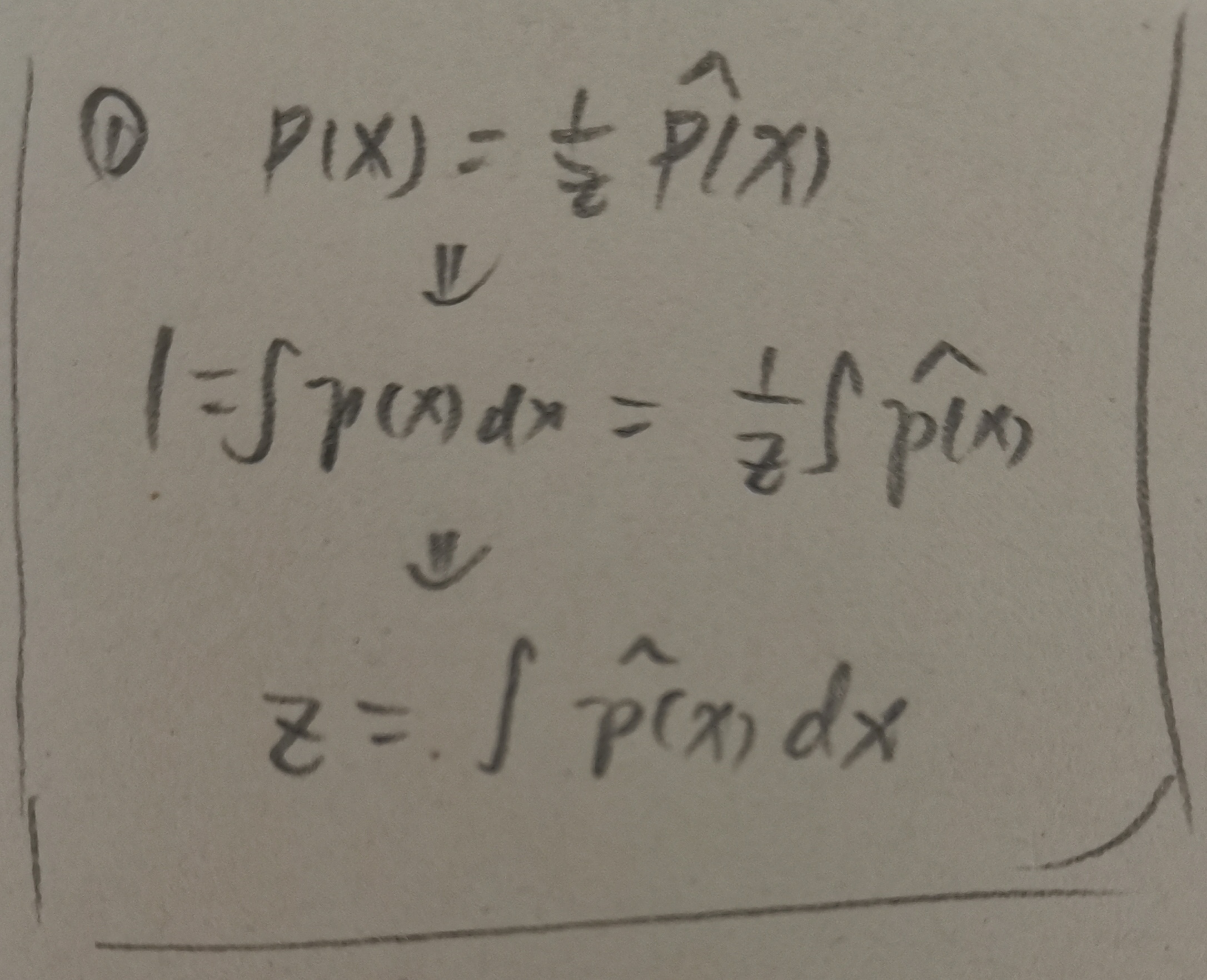
式①：配分函数Z（也叫作归一化因子）

　　　　　　　　A'(ita)和fai(x)的关系： A'(ita)=E(fai(x))，条件是p(x|ita)。

②由极大似然的想法推出 g_MLE=1/N(sum(fai(xi)))。

即从样本的充分统计量进行求和平均,就能得到参数向量值 g_mle。

 可以应用于广义线性模型(回归/分类)、概率图模型（RBM）、和变分推断（简便运算）中。

参考：

1.https://www.bilibili.com/video/BV1QW411y7D3?p=2，B站UP主：shuhuai008