强化学习：马尔可夫决策过程（模型参数、动态特性、价值函数概念、回溯图及贝尔曼期望方程推导）
马尔可夫决策过程：MDP
一、MDP模型表示
首先引出马尔可夫决策过程的几个相关变量集合：A={at},S={st},R={rt+1},t=1,2,...T or ∞。A表示Action，S表示State，R表示Reward，这几个均是静态的随机变量，可以是离散的，也可以是连续的。
①如果变量是离散的，且只有状态变量随时间变化，则可以用“状态转移矩阵”来表示这些随机变量之间的关系（比如HMM），状态转移矩阵就可以表达系统的动态特性；
②在MDP中，时刻t和时刻t+1变量间的关系不能再用“状态转移矩阵”表述，一个是因为变量是连续的，需要用一个函数来表示这些随机变量之间的关系（比如MDP），二是因为马尔可夫决策过程中的随机变量除了状态变量，还有动作变量和回报变量，不只有“状态转移”，所以应该用“动态特性”进行随机变量间的关系进行表述。
动态特性可以定量表述为函数P：动态特性函数是一个描述 t+1 和 t 前后两个相邻时刻的随机变量间动态关系的条件概率 ，可以用符号表述为 P=p(s',r | s, a) ，定义为p(s',r | s, a)=Pr(St+1=s'，Rt+1=r | St=s，At=a)。 【P:PROBABILITY ; R:RESTRICTED?】，其中P是函数空间。
如果要表达MDP的状态转移过程，可以将随机变量R求积分得到MDP的状态转移函数：p(s'|s,a)=Σr∈R p(s',r|s,a)。
所以整个马尔可夫决策过程的全部信息包含在状态变量集合A，S，R和函数空间P中，每个时刻都有一个At，St，Rt，每两个相邻时刻之间都有一个pt。
二、决策
决策过程就是寻找最优策略的过程。
=>分解成“策略”、“最优”、“寻找”三个关键字。
首先是策略（policy）：
策略形象的说法：在某时刻t，当St=s时，a的具体值：
抽象地说法：策略用于描述在某一时刻t,状态st和动作at的对应关系，根据这个关系是确定的还是随机的（有概率的随机），可以分为确定性策略和随机性策略。【策略是指是某一个时刻状态s对应的a？还是从初始时刻开始到t的所有s对应的a的取值序列？如果时间从1~T，每个时刻的at有5个可能取值{a1,a2,a3,a4,a5}，那么这个action序列就有5^T种可能。】
假定st固定取s(1)状态值，对应的a如果取确定值a(2)，那么就是确定性策略；对应的a如果是按照[0.1，0.8，0.1]的概率可能取a(1),a(2),a(3)的话，那么就是随机性策略。
| st | s(1) | s(2) | s(3) |
| at | a(2) | a(1) | a(3) |
标红的就是一个确定性策略，可以表示为 a=Π(s)。上表中的三个策略可以分别表示为a(2)=Π(s(1))，a(1)=Π(s(2))，a(3)=Π(s(3))。所以可以说在t时刻采取策略Π1=a(2),在t+1时刻采取策略Π2=a(3)...【所以策略是对应某一时刻的概念？】
| at,st | s(1) | s(2) | s(3) |
| a(1) | 0.1 | 0.7 | 0.1 |
| a(2) | 0.8 | 0.2 | 0.1 |
| a(3) | 0.1 | 0.1 | 0.8 |
标红的就是一个随机性策略，随机性策略可以表示为 Π (a | s)=Pr{At=a | St=s}。上表中的第一个策略可以表示为Π (a | s(1))=Pr{At=a(1) | St=s(1)}∪Pr{At=a(2) | St=s(1)}∪Pr{At=a(3) | St=s(1)}
然后是最优，要判断最优肯定需要有个指标，在MDP中我们呢已经用到了A和S，那么这个指标就是肯定和Rt+1有关，由此引出了回报的概念，回报用Gt表示。由于回报Rt+1是t时刻的动作At之后得到的反馈，所以需要考虑动作At的后效性（At对t之后的所有时刻都有影响），引入了Rt+2,Rt+3,...,考虑对后续时刻的变量影响效果的不同，引入了折扣因子γ，γ∈[0,1]，最终得到t时刻的回报：
Gt=F(Rt+1,Rt+2,...RT)=Rt+1+γRt+2+γ2Rt+3+...+γT-1RT。
这里需要明确Rt+1也是个随机变量，比如Rt+1={r1,r2,r3}有三种取值，并且每种对应有一定的概率p={0.7 0.2 0.1}。那么可以看到由于at和Rt+1都是随机变量，那么从t到t+1时刻经过决策at，奖励Rt+1就对应有3x5个Gt，分别为{Gt1,Gt2,Gt3,...,Gt15}。由此我们可以看出，概率图模型中的指标和机器学习中其他的指标不太一样，需要考虑变量是个服从某个概率分布的随机变量，所以这里的衡量t时刻决策好坏的定量指标是Gt对Π求期望，这就引出了价值函数的概念。
价值函数vΠ 定义为 EΠ Pr (Gt |St=s) ，那么该期望的具体公式是什么？加权平均的权是指的什么?概率？这就引出了贝尔曼期望方程，推导如下：
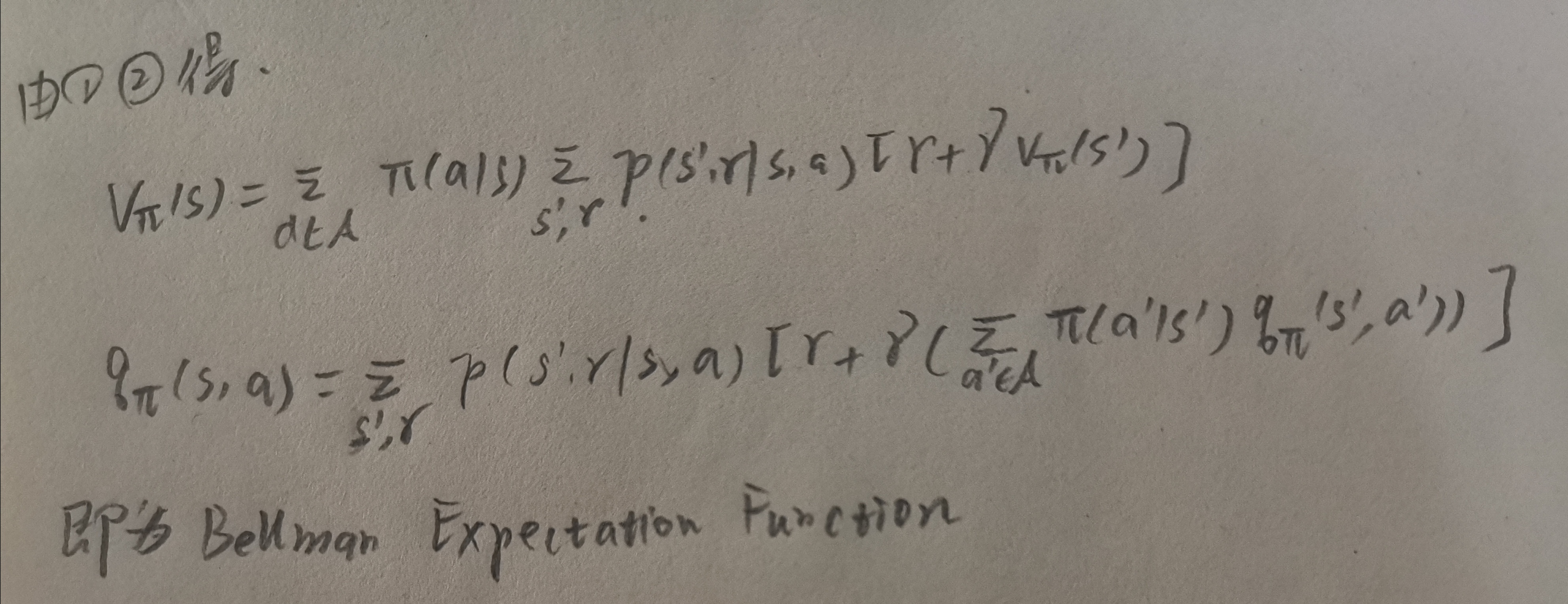
问题：
1.Π是St取值s的函数？与t无关？
参考资料：
1.https://www.bilibili.com/video/BV1RA411q7wt?from=search&seid=4107546504069376636，作者：shuhuai008.
2.https://www.bilibili.com/video/BV1RA411q7wt?p=5，作者：shuhuai008
