强化学习:MDP(Markov Decision Process)
0.强化学习(reinforcement learning),特点是引入奖励机制。【强化学习属于机器学习框架中的什么部分?】
1.引出MDP的思路
=>Random variable
=>Stchastic Process
=>Markov chain/Process
=>Markov Reward Process
=>Markov Decision Process
2.随机变量(Random variable)
强化学习是引入了概率的一种算法,随机变量是研究对象,比如随机变量S1。
【随机变量常用大写字母表示,随机变量的具体取值常用小写字母表示,P(S=s)表示变量S取s值的概率】
关于随机变量有几个问题需要回答:
这个随机变量是服从于哪种概率分布?
这个概率分布对应的概率密度函数什么?
这个随机变量是离散分布还是连续分布?
是一维随机变量还是多维随机变量?
不同的随机变量之间是什么关系?
以下针对这几个问题尝试进行回答。
概率分布(prob dist)是指用于表述随机变量取值的概率规律。随机变量的概率分布指的是随机变量的可能取值及取得对应值的概率。
概率分布有几种类型,最常见的是高斯分布(即正态分布)【此外还有0-1分布等等】。若随机变量X服从于期望为u,协方差为Σ的高斯分布,则写作X~N(u,Σ)
每种分布对应的有一个概率密度函数(probability density function:PDF),高斯分布的概率密度函数如下:
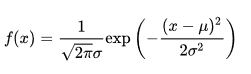
其中,u是期望,σ2是协方差。【均值和方差是X为一维变量时期望和协方差的描述方式】。
随机变量离散分布含义是X的取值是离散的。随机变量连续分布含义是X的取值是连续的。
X={x1,x2,x3,...}是一组由一维随机变量组成的集合;
Y={y1,y2,y3,...}是一组由高维随机变量组成的集合;
期望和方差/协方差都是表示一组变量的数字特征。
X和Y期望和方差/协方差公式如下:
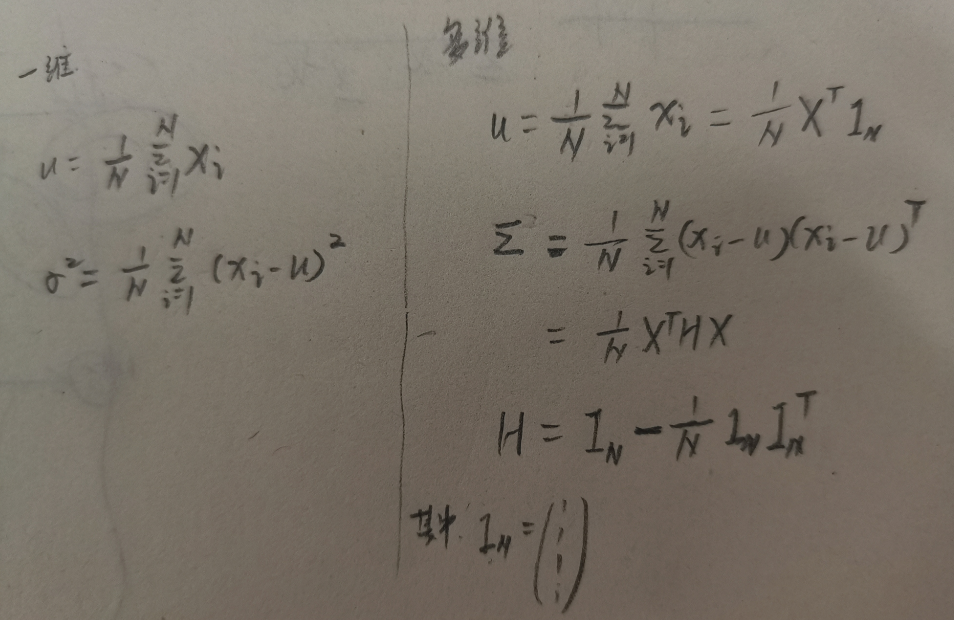
不同的随机变量之间的关系,可以根据不同模型的假设进行分析。比如Naive Bayes中,假设在Y被观测的前提下,x1,x2...xN之间两两条件独立。比如在HMM中就有观测独立假设和一阶齐次Markov假设。观测独立假设中X(t+1)只和Z(t+1)有关(也就是在Z(t+1)被观测的情况下,X(t+1)与其他随机变量条件独立)。一阶齐次Markov假设中Z(t+1)只和Z(t)有关(也就是说在Z(t)被观测的情况下,Z(t+1)与其他随机变量条件独立)。HMM中的Markov假设是”一阶“齐次Markov假设,如果是”二阶“Markov假设的话,Z(t+1)只和Z(t),Z(t-1)有关(也就是说在Z(t),Z(t-1)被观测的情况下,Z(t+1)与其他随机变量条件独立)。
3.随机过程(Stchastic Process)
变量之间关系复杂,没有明显的可循规律。
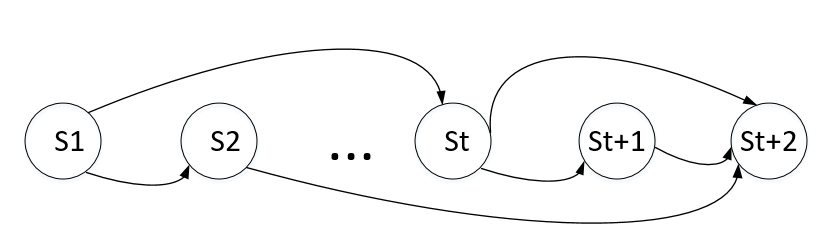
4.马尔可夫链/马尔可夫过程(Markov chain/Process)
马尔可夫过程(Markov chain)是一个具有Markov性质的特殊的随机过程(stochastic process)。
一阶马尔可夫假设:已知st的情况下,st+1与s1,s2...st-1均无关。(即st+1只与st有关)。

5.马尔科夫奖励过程(Markov Reward Process)

其中 St是t时刻的状态变量,Rt+1是对应t时刻的Reward。
6.马尔可夫决策过程(Markov Decision Process)

其中 St是t时刻的状态变量,At是Action,Rt+1是对应t时刻的Reward。
问题:如何与隐马尔可夫结合?
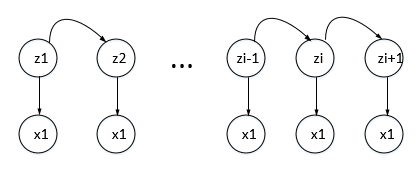
隐马尔可夫是为了对概率进行分布求解,从而引入隐变量的概念,将s1作为隐变量,x1作为观测变量。
参考资料:
1.https://www.bilibili.com/video/BV1RA411q7wt?from=search&seid=4107546504069376636,作者:shuhuai008

 浙公网安备 33010602011771号
浙公网安备 33010602011771号