概率图:HMM:Evaluation问题(前向算法/后向算法)
一、HMM:一个模型,两个假设,三个问题。
思路:HMM=>在机器学习大框架中的位置=>模型参数(示意图及定义)=>模型假设=>模型的应用:三个问题(及其数值求解算法)=>各个问题的具体应用场景(看文献)

(来源:B站up主,shuhuai008,板书)
前向算法后向算法公式推导思路:
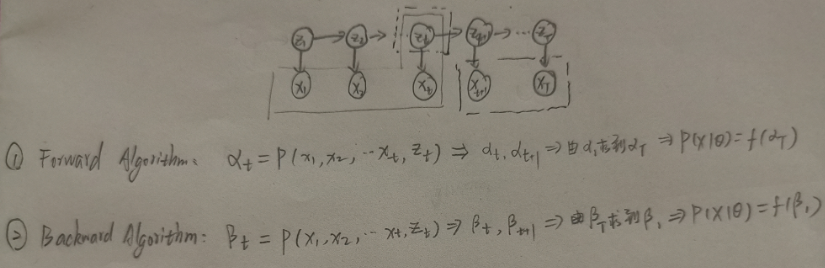
二、求解Evaluation问题的前向算法:

(来源:B站up主,shuhuai008,板书:前向算法公式推导)

拆分P(O|λ)思路:
将P(O|λ)用积分求和形式拆解,引入I,再用联合概率公式进行进一步分解,再分别求。P(O|λ)=ΣI P(O,I | λ)=ΣI P(O, | I, λ) P( I | λ),分别求解P(O, | I, λ) 和P( I | λ),用αij和bj(k)表示,推出P(O|λ)的公式,按照该公式计算,复杂度为O(NT),计算时间随着时间 t 的增大,呈指数型上升,运算效率低,所以引入前向算法(和后向算法)进行计算。

前向算法公式推导
前向算法备注:
②引入记号:αt(i)=P(o1,o2,...,ot,it=qi | λ),结合示意图理解其含义,其中,t表示当前为t时刻,i表示t时刻对应的状态变量it取qi值,即it=qi。
由于αT(i)=P(o1,o2,...,oT,it=qi | λ)=P(O,it=qi | λ),正好存在P(O|λ)=sum【P(O,it=qi | λ)】,所以如果可以通过对αT(i)关于it=qi,i=1到N求和,就能得到P(O|λ)。
③对αt+1(j)进行公式(拆解)推导,找到αt+1(j)和αt(i)的递推关系:αt+1(j)=Σ1N bj(ot+1)aijαt(i) .
④Evaluation问题是给定λ=(pi,A,B),即给定{a1(1),a1(2),...,a1(N)}={q1,q2,...qN},状态转移矩阵A给出{a11,a12,...,aNN}、发射矩阵B给出{b1(o1),b2(o1),...bN(o1)},根据递推公式,推出{a2(1),a2(2),...,a2(N)},然后继续根据迭代,一直推到{aT(1),aT(2),...,aT(N)},然后对i从1到N求和得到P(O|λ)。
⑤前向算法的复杂度为O(T*N^2)。
三、求解Evaluation问题的后向算法:
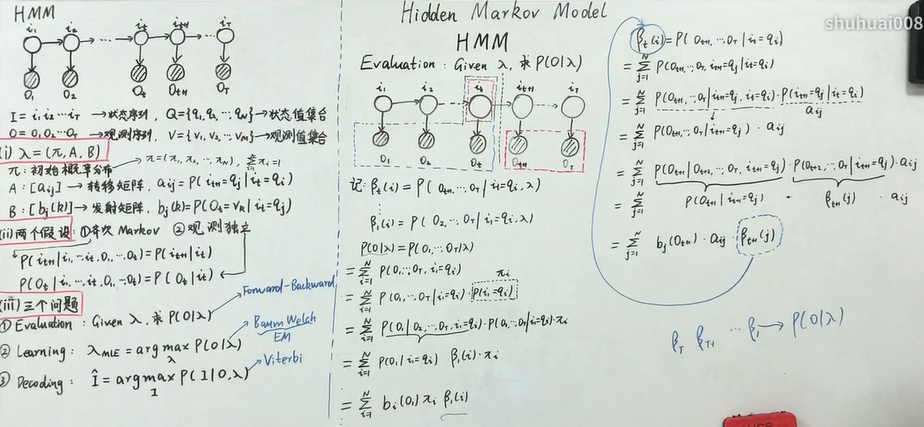
(来源:B站up主:shuhuai008,板书:后向算法递推公式)

后向算法公式推导
后向算法备注:
推导过程中主要用到:
①联合概率公式P(A,B)=P(A|B)P(B);P(A,B|C)=P(A|B,C)P(B|C)
②独立观测假设,ot只与it有关。【bj(k)】
③齐次Markov假设,it+1只与it有关。【aij】
④概率图全局Markov性质(head-tail)模块的条件独立性判断,⭕a—>⭕b—>⭕c,若b被观测,则a,c条件独立。可将a,b,c分别看作it,it+1,ot+1。则P(ot+1|it,it+1)=P(ot+1|it+1)。
后向算法的复杂度也是O(TN^2)。
参考资料:
1.https://www.bilibili.com/video/BV1MW41167Rf?p=2 ,作者:shuhuai008


