概率图：GMM求解：EM优化算法的导出（从【ELBO+KL】和【ELBO+Jensen】两个角度导出）

根据logP(X|θ)的两种分解方式，从两个角度导出EM公式：

 

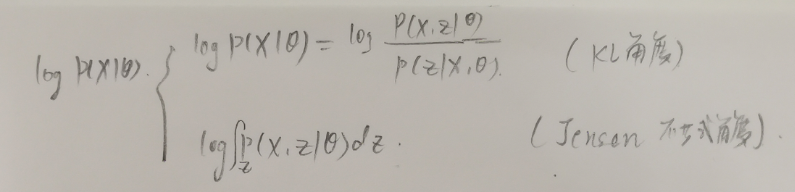
一、从（最大化ELBO，最小化KL散度）角度导出EM公式：

                                                                              （来源：B站up主：shuhuai008,板书）

备注：

argmaxP(X|θ)=argmaxELBO<=>minimize KL<=> q(z)=P(Z|X,θ) 【固定X时，要想最大化ELBO，就需要最小化散度KL，最小化KL得到后验条件P(Z|X,θ)】

由于是在每一次（E-step，M-step）迭代中求解argmax，所以需要加上(t)标注，成为P(Z|X,θ^(t))。

 

二、从（最大化ELBO，Jensen不等式角度）导出EM公式

                                                                                （来源：B站up主：shuhuai008,板书）

备注：几个变换的小技巧：

①将P(X|θ)表示成关于Z的积分（期望） 【从另一个角度对P(X|θ)进行分解】

②引入概率q(Z)【重要】

③Jensen不等式“=”成立条件：log(mmm)中的mmm为常数。

④通过条件概率公式变换出q(Z)=P(Z|X,θ) => 导出公式

 

三、广义EM【后验P(Z|X,θ)不好求的时候，EM的公式】

                                                                                 （来源：B站up主：shuhuai008,板书）

备注：

①ELBO=L(q,θ)

②求解后验概率困难，所以提出了变分推断（variational inference）、蒙特卡洛算法(MCMC)等等

 

四、EM变种算法

可以用近似推断的方法求解后验，近似推断有变分推断和蒙特卡洛采样

VBEM/VEM（variational Bayes Expectation Maximun）基于平均场理论的变分推断求解后验P+EM

MCEM：蒙特卡洛采样推断求解后验P+EM

VB：variational bayes

VI：variational inference

VB和VI基本一样。

各种算法的使用场景？=> 看文献

参考资料：

1.https://www.bilibili.com/video/BV1qW411k7ao?p=2 ，作者：shuhuai008