概率图：高斯混合模型（GMM）
高斯混合模型（Gaussian Mixture model）
来源：B站up主：shuhuai008，板书
问题：“高斯”？，“混合”？
可从两个角度理解
一、从几何角度看：高斯混合模型就是若干个高斯模型的“加权平均”。
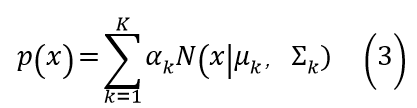
混合高斯分布的公式
此处的x（小写）可以指代任意一个样本xi，利用公式（3）可以求解出xi的概率密度函数。
二、从“生成”/“混合”的角度看【个人理解：“混合”体现在高斯分布的叠加，也体现在“隐变量”和观测变量的引入】
GMM模型的概率图表示，及相关概念示意图
z是“隐变量”，x是观测变量，由隐变量生成观测变量的过程就是混合高斯模型的生成过程。x在概率图中用阴影表示可观测。N表示有N个样本{x1,x2...xN}，对应的也就有N个隐变量{z1,z2,...zN}。z1表示第一个样本的隐变量，z1是一个离散的随机变量，z1的概率密度函数如下所示。
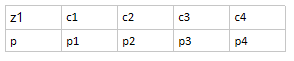
z1中，p(c1)=p1，p(c2)=p2,...p(ck)=pk；所以将pz1表示成p={p1,p2,...pk}，找出pz1中最大的概率，假如max{p1,p2,...pk}=p4 ，那么z1=c4 ，表示z1属于第4个高斯分布的概率最大=>x1服从于第四个高斯分布，写作x1~N（u4,Σ4）。其实z1就相当于一个指示变量。其中c1,c2,...ck分别是各个高斯分布的中心点（c1..ck和x1,...xN的向量维度相同，此处可类比聚类算法中的聚类中心）。
离散随机变量Z理解：
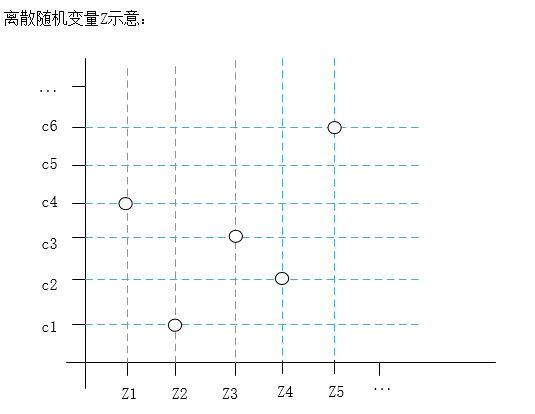
“离散”指的是z1的值域是离散的数值{c1,c2...ck}，只能从这几个中选，比较形象的说就是z1可以在y轴方向上一个网格或多个网格的”跳动“。
“随机”指的是z1取c1，c2,...ck等数值的概率是确定的，但是在某一个样本的观测中具体取哪个c是随机的。【个人理解】
观测变量x理解：
观测变量x可以是连续的，也可以是离散的,x服从于某个特定的高斯分布。【具体服从于哪个见上文】
验证两个角度求解p(xi)概率是否“殊途同归”
1.几何角度：
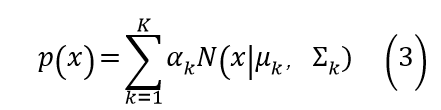
2.生成角度：
“极大似然”法尝试求解模型参数（解析法）：【因为行不通，所以引出用数值解法：EM法】
来源：B站up主：shuhuai008，板书
其中，X（大写）包括{x1,x2,...xN}所有样本的观测变量，Z代表{z1,z2,...zN}所有样本的隐变量；
θ={p1,p2,...pk, u1,u2,...uk,Σ1,Σ2,...,Σk} 表示的是一个样本xi(小写)的模型参数，θ_hat指的是所有样本的参数{θ1,θ2，...，θN}。
备注：
GMM和Naive Bayes 的样本均满足独立同分布假设，即所有样本{x1,x2,...xN}两两独立同分布（iid）
参考资料：
1.https://www.bilibili.com/video/BV13b411w7Xj?p=2，作者：shuhuai008
