《机器学习基石》笔记（二）（台大林轩田版Lecture2）

2.learning to answer yes/no【{-1，1}二分类】

示例：如何构造一个二分类的线性分类器。

内容如下：

 2.1 感知机的假设集H（hypothesis set）

假设集中存在非常多个预测函数，“perceptron”预测函数是其中的一种，我们选择“perceptron”

函数作为其中下面示例的预测函数，“perceptron”预测函数的数学表达形式如下：

 “perceptron”预测函数的数学形式可以向量化为如下形式：

注意区别直线方程和“perceptron”预测函数，直线方程为 W^TX=0，“perceptron”预测函数h(x)=sign(W^TX)。

有时候简略讲直线就是感知机预测函数，这其实是不准确的。感知机应该包括“在直线右边，分为正类；

在直线左边，分为负类”这一层信息，所以感知机为h(x)=sign(W^TX)，该感知机也称为一个二分类器，由

于W^TX=0为线性函数，所以也是一个"线性"分类器。

 

“perceptron”预测函数应用于拥有两维特征的数据中，也就是在二维空间中将数据分开，可视化

如下所示，直线将平面分为两部分，蓝色部分为预测函数判断的{+1}类，红色部分为预测函数判

断的{-1}类，（如果是在高维空间中，  “perceptron”预测函数则是一个超平面分类器）。如果所有

可能的直线有{line1,line2,...linen}，那么假设集为H(x)={sign(line1),sign(line2),...sign(linen)}，假

设集就是空间内所有可能的直线代表的分类器的集合。

2.2 感知学习算法（Perception Learning Algotirhm：PLA）

由于H(x)假设集中有几乎无数个"perceptron"预测函数，简单讲就是平面中将样本分为两类的直线

有无数条，那么如何找出其中分类效果最好的直线呢？分类效果最好指的是分类非常接近原样本

分类，甚至和原样本分类一模一样。找出最优直线(g₀)的算法就是感知学习机算法（PLA）。

PLA算法的思想是先随机给定一个g₀=W₀^TX，然后计算误差，通过误差修正的方法逐步得到最优的

直线g_opt。修正直线的过程其实就是逐步得到最优的权重系数向量W*的过程。

如何保证直线的修正一直是朝着好的方向进行的呢？这就涉及到PLA的修正规则，PLA修正规则

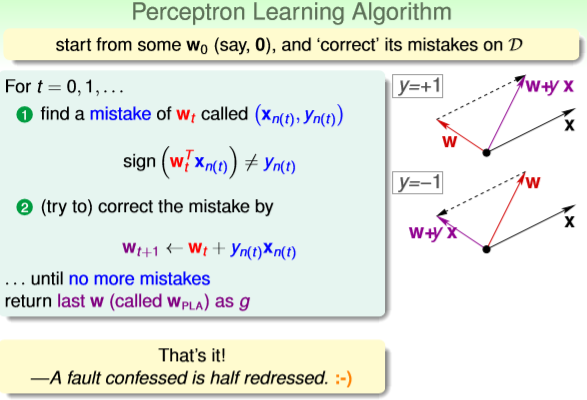
为下图公式①②，具体解释为：在迭代第t+1步，根据被g_t直线分类错误的某一个样本(x_n(t),y_n(t))，

利用W_t+1=W_t+y_n(t)*x_n(t)公式，得到本次迭代的W_t+1，得到本次迭代的直线W_t+1X=0。那么如何

保证②公式能使得W在朝着好的方向迭代呢？②公式是能够实现修正功能的一个规则，具体合理

性可以通过下图的右半部分示意图解释：将Wt简略表达为W，将x_n(t)，y_n(t)简略表达为x，y，将

W_t+1简略表达为W+yx，W和x均为一个向量，y是错误分类的结果{+1}或{-1}。如果(x,y)原本为正

类，y={+1}，在第t次迭代中sign(W_^tx)<0被错分类，那么在下一轮迭代，需要修正这个错误，也就

是要求W_t+1x>0，两个向量内积大于0，也就是两个向量间的夹角小于90°，如下图右上方示意图

所示，修正后的Wt+1（W+yx）向量与x向量间的夹角由原来的大于90°变为小于90°，说明公式②

能修正被错误分类的样本。y={-1}情况同上，可以自己推导。

直到检测完所有样本，发现没有样本被错误分类后，算法停止迭代，此时得到的W为W_PLA，对应的

h(x)=sign(W_PLAx) 就是要找的 g。

那么在实际算法运算中，错误样本怎么选呢？错误样本的周期性选取有两种方法，一种是按照1~n的

顺序周期选取，称为naive cycle，另一种是随机选取错误样本，称为precomputed random cycle。

PLA算法迭代过程的可视化如下：

首先算法w₀=0，随机选定一个样本，因为正确分类必须为{+1}或{-1}，但w0=0输出结果为0，所以

显示样本分类错误。将该样本进行错误修正，得到w1=0+1*x1=x1，如图1紫色线条所示，w1是对

应的直线的法向量（直线表示为wx=0），所以与w1对应的直线为与w1垂直的直线，如图2所示。

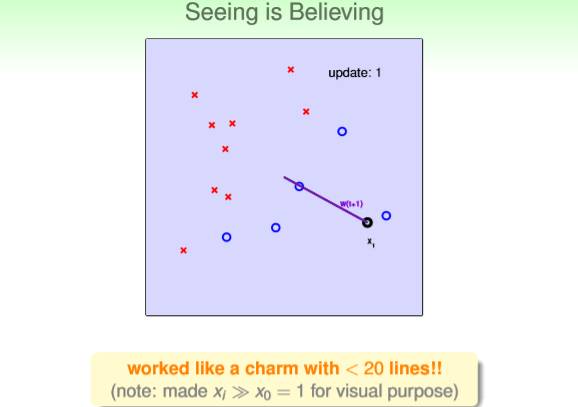
 　　　　　　　　　　　　　　      图1

图2中红线表示上一轮的wt，黑线表示选择的被错分类的样本x0，②PLA公式表明，根据错分

类样本x0和上一轮权重向量wt，得到下一轮迭代得wt+1，如紫线所示，wt+1对应的直线为图3

中红色部分和蓝色部分的分界直线。

                                                              图2

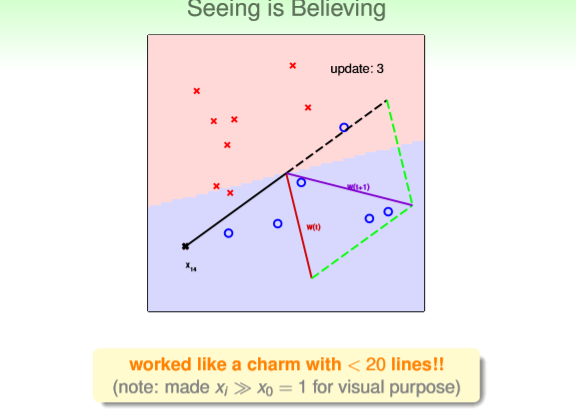
　　　　　　　　　　　　　　　　　　　　图3

迭代9次后得到图4

　　　　　　　　　　　　　　　　　　　　图4

迭代至第十次，找到使全部样本都正确分类的直线如图final所示

 

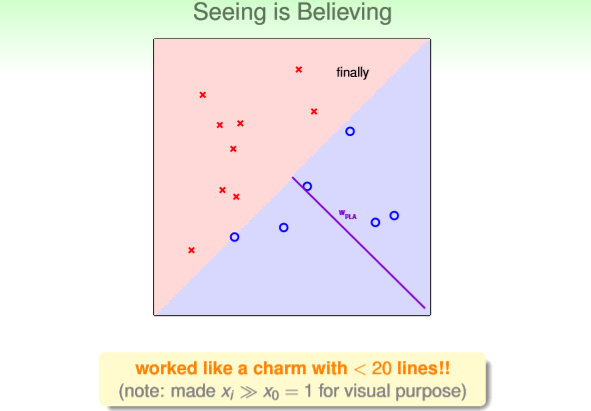
　　　　　　　　　　　　　　　　　　图final

2.3 PLA是否收敛到最优（算法是否能够收敛（halt）？，如果能够收敛，最终得到的是不是最优？）

PLA存在如下问题：算法是否一定能够停止？最后得到的g是否一定接近f

第一个问题：PLA算法是否一定能够停止？答案是只有数据使线性可分的情况下，PLA算法才能停止。

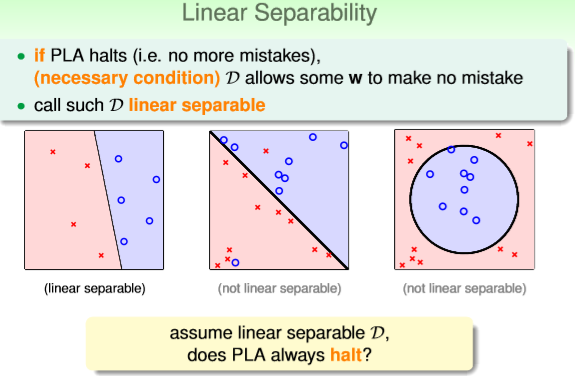
PLA停止迭代的条件使找到一条直线将所有样本正确分类，如果样本原本就是线性不可分的样本，那

么PLA就回一直迭代下去，算法无法得到好的结果。如下图所示为线性可分，线性不可分，线性不可

分的样本情况。

第二个问题：如果算法能够收敛，那么最终得到的是不是最优？也就是在每一次的迭代过程中，

wt是不是在向wf逼近（wf是理想预测函数f的权值向量）。答案是wt在迭代中确实在向wf逐步靠

近。理由如下图所示：图中w_f^Tw_t+1总是大于w_f^Tw_t，由于在两个向量大小几乎不变的情况下，两

向量内积越大，说明两个向量方向越靠近，所以w_t+1比w_t更接近w_f。说明迭代过程中w确实在逐

渐的优化。

前文提到两向量内积越大说明两向量方向越接近的情况存在前提，就是两向量的大小几乎不变，

下面阐述为什么_wt到w_t+1的大小变化很小。如下图所示，两者的平方差总是小于||xn||^2，所以

“变化很小”的前提成立。

2.4 线性不可分的数据

下图为对于PLA算法的小总结

改进的PLA算法（pocket algorithm）：能够容忍一定程度的噪声数据

2.5 关于lecture2 的小总结

 参考资料：
1.B站视频：https://www.bilibili.com/video/BV1Cx411i7op?p=9 ：p5~p9