数据集划分：交叉验证

一、简单划分：数据集：测试集=7：3

问题：

1）.没有充分的利用数据集；

2）.回归问题中的MSE（mean square error）受到划分比例的影响，导致最终模型的最优参数选择也受到划分比例的影响。

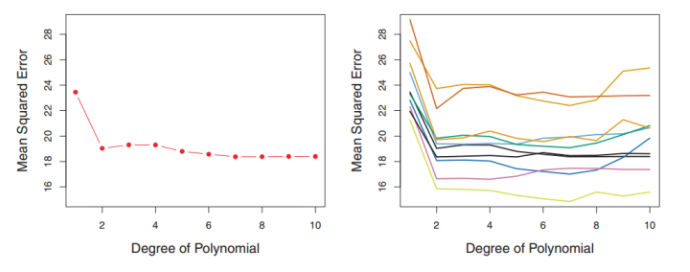
【图来源：https://zhuanlan.zhihu.com/p/24825503?refer=rdatamining】

右侧是10种数据集划分方法得到的"不同阶次的多项式模型—均方差"图

可以看到，不同的数据集划分方式，达到最小MSE的多项式模型是不同的，所以这种“一刀切”的简单数据集划分方法不够合理。

 

二、LOOCV（leave-one-out cross validation）

每次选取1个样本作为测试样本，其余n-1个作为训练样本。若为回归模型，分n次进行MSE计算，最终MSE取均值。

优点：不受数据集划分方法的影响；

缺点：计算量太大，计算成本是简单划分的n-1倍。

 

三、k折交叉验证（k-fold cross validation）

1.k取值：

一般取k=5~10；

考虑k对bias（可表征模型对样本的拟合精度）和variance（可表征模型泛化能力）的影响，k越大，bias越小，variance越大；k越小，bias越大，variance越小。所以为了平衡bias和variance，一般选取k=5~10。【bias大，模型欠拟合，variance大，模型过拟合，所以k的选取关系到模型的欠拟合和过拟合】

2.k折交叉验证含义：

若k=5，将数据集分成5份，每次取1份作为测试集，其余4份作为训练集。若为回归模型，分5次进行MSE计算，最终MSE取均值。

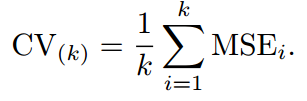
若为分类模型，分五次进行错分类统计，最终错分类个数取均值。

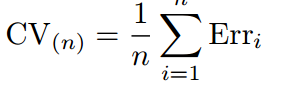
【Erri是第i组测试集中错分类的个数。】

 

 3.k-fold CV 优点

兼具简单划分和LOOCV的优点：不受数据集划分方法的影响（LOOCV）；且计算量小（简单划分）

 

4.k-fold CV 精度

【图来源：https://zhuanlan.zhihu.com/p/24825503?refer=rdatamining】

图中，红线代表k折验证，黑色虚线代表LOOCV。【LOOCV可看作k=N的交叉验证】

 

参考资料：

1.机器学习：交叉验证详解，https://zhuanlan.zhihu.com/p/24825503?refer=rdatamining，作者：文兄