决策树(二)：信息增益（率）/gini系数&评价函数&交叉验证
一、决策树不同算法信息指标：
发展过程：ID3 -> C4.5 -> Cart;
相互关系：ID3算法存在这么一个问题，如果某一个特征中种类划分很多，但是每个种类中包含的样本个数又很少，就会导致信息增益很大的情况，但是这个特征和结果之间并没有很大的相关性。所以这个特征就不是我们最终想优先决策的特征【这是ID3以信息增益作为指标的一个bug】，为了解决这个问题，引出信息增益率的概念，对应基于ID3的改进算法C4.5算法。
①信息增益（ID3算法）：
简单易懂，适合大部分场景；
但是因为分割越细错分率越低，效果越好的原因，所以存在分割太细造成对训练数据的过拟合问题，使得对测试数据的泛化效果差。
最高效的方案为根据各个特征的信息增益从大到小排列得到方案（特征的决策顺序）。
计算效率高；
②信息增益率（C4.5算法）：
信息增益率=某特征对于总体数据的信息增益 / 该特征自身的熵值
对ID3算法的改进：除了指标变化，其他部分大同小异；
信息增益率可以避免分割太细；【如果分割太细坟墓相应也会增加，信息增益率减小，该特征就不会被优先选中。】
最高效的方案为根据各个特征的信息增益率从大到小排列得到方案。
计算效率较低；
③基尼系数（Cart算法）：
基尼(gini)系数：总体内部包含越混乱，基尼系数越大；内部纯度越高，基尼系数越小。
基尼系数公式：
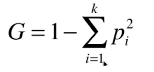
k为某节点中包含样本的种类数目；
pi为某节点中某类样本数目 / 该节点中样本总数。
基尼系数计算示例：
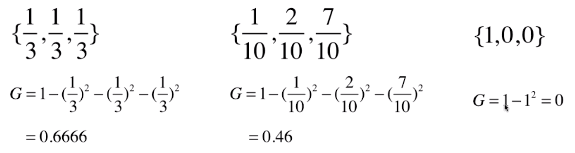
最高效的方案为gini系数最小的方案。基尼系数越小，不确定性越小；
但也存在分割过细，容易造成过拟合的情况；通常利用剪枝操作处理；
计算代价高。【可采用特定方法降低计算代价】
二、决策树的“代价函数”——评价函数
所谓决策树的“代价函数”其实就是一个对决策树最优化的定量表述。
评价函数：C(T)=sumi∈leaf [ Ni*H(t) ];
评价函数中的Ni 是每个叶子节点中样本的个数，在这个公式中相当于权重；H(t)是每个叶子节点的熵值；
评价函数越小越好，为什么呢？因为评价函数中H(t)表示熵值，对于每一个叶子节点我们是希望他的熵值越小越好的，也就是纯度（一个节点内包含的样本种类少）越高越好，纯度越高表明分类效果越好【叶子节点就是没有子节点的节点】
三、对数据集的利用：交叉验证法：cross-validation
【3 folds cross validation：训练集：测试集=2：1（从3份中选1份：可以是随机采样，然后按比例划分数据集）】
10 folds cross validation : 训练集：测试集=9：1（从10份中选1份：可以是随机采样，然后按比例划分数据集）
第一次：选1作为测试集，选2~9作为训练集；
第二次：选2作为测试集，选1，3~10作为训练集；
...
最后，取平均错分率作为总的错分率；
参考资料：
1.https://zhuanlan.zhihu.com/p/30059442，作者：犀利哥的大实话
2.https://www.bilibili.com/video/BV1Ps411V7px?p=5，作者：蓝亚之舟
3.https://www.cnblogs.com/volcao/p/9478314.html，作者：volcano！ 【相关代码】
