数学建模：logistic拟合 &一阶微分方程求解正规/混合战争模型(matlab代码)

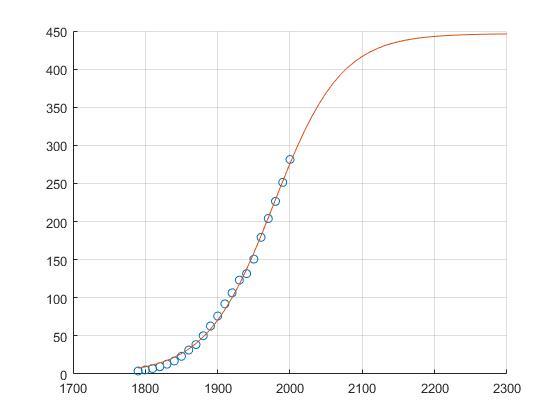
x=[1790:10:2000];
y=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 150.7 179.3 204.0 226.5 251.4 281.4];
x=x';y=y';                  % 将原始数据转换为列向量
st_ = [500 20 0.2];         % xm,b,r 设定初始值
ft_ = fittype('xm/(1+b*exp(-r*(x-1790)))','dependent',{'y'},'independent',{'x'},'coefficients',{'xm', 'b', 'r'});
cf_ = fit(x,y,ft_ ,'Startpoint',st_)
% 模型输出的拟合参数
xm = 446.6;    % 拟合出的最大人口数量xm
b = 57.01;     % b=xm/x0;
r = 0.02155;   % 拟合出的人口增长率r
% 画图       
scatter(x,y);  % 散点图
hold on;
x1=[1790:10:2300];  % 检验查看拟合曲线是否为S型曲线
cf_ = xm./(1+b*exp(-r*(x1-1790)));
plot(x1,cf_);
grid

 

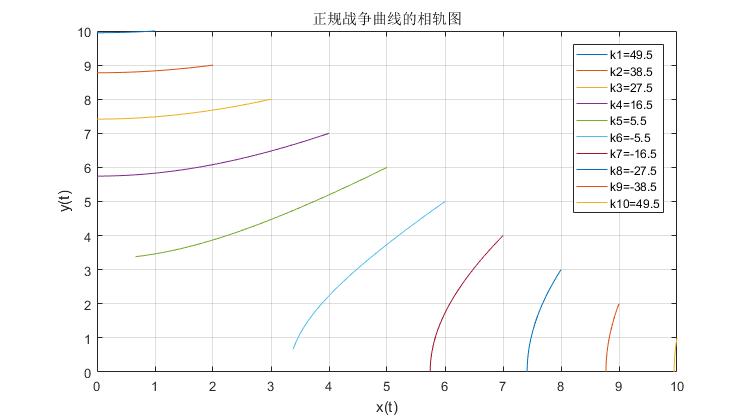
%例子1：正规战争（课本p150）
%模型类型：一阶微分方程组
%数值解法：RK4:ode45()
%% f1.m
function dz=f(t,z)   %z=[x,y]
a=0.5;  %甲方战斗系数
b=0.5;  %乙方战斗系数
dz(1)=-a*z(2);
dz(2)=-b*z(1);
dz=dz(:);
end
%% lizi1.m
x0=[1:1:10];   %甲方兵力变化
y0=[10:-1:1];  %乙方兵力变化
for i=1:10
    [t,z]=ode45(@f,[0:0.02:2],[x0(i),y0(i)])
    k(i)=0.5*y0(i)^2-0.5*x0(i)^2;  %a=0.5,b=0.5,计算k
    plot(z(:,1),z(:,2));
    axis([0,10,0,10]);
    hold on
End

%模型：混合战争：甲方游击部队，乙方正规部队（课本p152）
%模型类型：一阶微分方程组
%数值解法：RK4:ode45()
function dz=f(t,z)   %z=[x,y]
c=0.5;  %甲方战斗系数
d=0.5;  %乙方战斗系数
dz(1)=-c*z(1)*z(2);
dz(2)=-d*z(1);
dz=dz(:);
end

%%混合战争模型
%f2.m
function dz=f2(t,z)   %z=[x,y]
c=0.5;  %甲方战斗系数
d=0.5;  %乙方战斗系数
dz(1)=-c*z(1)*z(2);
dz(2)=-d*z(1);
dz=dz(:);
End

%Lizi2.m
x0=[1:1:10];   %甲方兵力变化
y0=[10:-1:1];  %乙方兵力变化
for i=1:10
    [t,z]=ode45(@f1,[0:0.02:2],[x0(i),y0(i)])
    n(i)=0.5*y0(i)^2-2*0.5*x0(i);  %c=0.5,d=0.5,计算n
    plot(z(:,1),z(:,2));
    axis([0,11,0,11]);
    hold on
end

参考资料：

https://zhidao.baidu.com/question/163154587.html