神经网络(二):反向传播步骤(BP)
BP神经网络基本概念:
1.代价函数:神经网络的训练过程就是通过代价函数最小化(J)拟合出最优参数(weight)
【神经网络的代价函数其实就是一个指标,表明用模型对样本的拟合程度,可以类比成模型的预测值h(x)和样本输出yi的差值的方差(待确定)】
【代价函数最小化可以通过梯度下降法或者反向传播算法实现。分析两者优劣】
【神经网络的代价函数是一个非凸函数,意味着使用优化算法有可能会陷入局部最优解】
【代价函数中的正则项如何理解;可以对比ogistic回归公式中正则项功能(避免参数过拟合)】
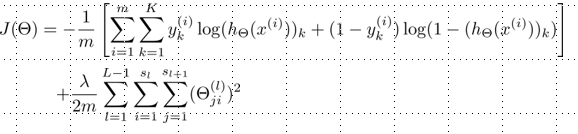
2.反向传播(Backpropagation)过程描述:
i) 将前向传播中得到的神经元值和权重值、最后一层输出值(预测值hi和样本值yi的误差作为输入,
ii) 计算出隐藏层中各个神经元的误差,累计误差;【相关公式计算】
iii) 输出为代价函数J(theta)对权重theta_i的偏导数。

吴恩达机器学习反向传播过程中的误差计算
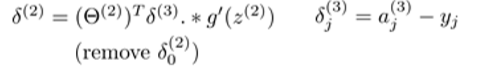
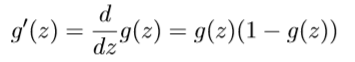
各层各个神经元误差详细公式
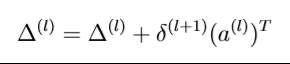
累计误差公式

不带正则项的偏导数公式
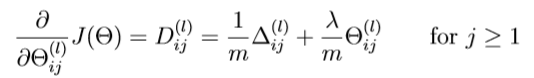
带正则项的偏导数公式

吴恩达机器学习反向传播算法伪码
3.向量展开:神经网络训练过程中参数向量/矩阵的转化。【作为优化算法的输入时,参数转化为向量;作为前向/反向传播输入时,参数采用矩阵形式】
参数的向量和矩阵转换的matlab实现

向量转换在算法中的应用位置
4.梯度检验:因为反向传播过程中结果可能会表面看起来合理【合理指的是代价函数在优化过程中变小】,但其实是存在bug的,导致有bug的BP算法和没有bug的BP算法误差可能会比较大。所以需要有梯度检验的步骤,梯度算法和BP算法的作用相同,都是算出代价函数J(theta)的偏导数,但是梯度法过程中不容易出现误差,但是运算慢;BP算法实现过程中容易出现错误,但是运算快;所以在编程实现BP算法时,用梯度算法算出的偏导数和BP算法得出的导数值相比,看是否基本相等(只有几位小数的差别)【所谓梯度检验】。在确定BP程序没有错误后,再用来进行神经网络的训练【训练过程中用BP算法,不用梯度算法】

梯度法:某一点导数的数值逼近
![]()
梯度法matlab公式
![]()
对向量形式的theta求偏导

关于梯度检验的意见
5.随机初始化:常见的初始化是将所有参数初始化为0,但是如果在神经网络算法中零初始化会导致:上一层传输给下一层第一个神经元的所有参数和上一层传输给下一层第二个神经元的所有参数完全一样,进而导致单个层中的每个神经元值都是一样的,导致特征冗余。并且反向传播过程中同一层各个神经元的误差也完全一样,进而偏导数也完全一样。
【单个神经元可以看作是新构造的一个复杂特征】
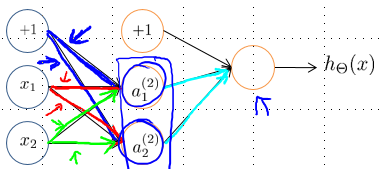
若零初始化,则同色系的权重参数相等

随机初始化的matlab实现【epsilon可以取10^-4】
6.神经网络框架构建:输入层unit个数有样本的特征数决定;隐藏层层数一般为一层,也可以是2、3、4层等,层数越多表示神经网络越深,计算量越大;隐藏层单层unit个数一般是输入层unit的倍数,可以是1、2、3倍等;unit个数越多,重构特征越多,能够拟合出越复杂的非线性函数,但是计算代价越大。
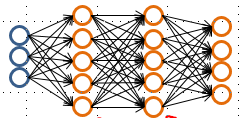
神经网络常见框架
7.训练一个神经网络步骤
①随机初始化权重系数theta
②前向传播算法计算出h(xi)和各个unit参数值ai(l);
③计算出误差最后一层的误差δ(final_l),再利用反向传播算法计算出各层的unit的误差δi(l)
④公式求出每层误差Δ=Δ’+δ*(a)T和代价函数的偏导数,输出Dvec【differential vector】
⑤梯度算法检验BP算法的准确性
⑥将前向传播和反向传播结合,用优化算法对代价函数求解最小值。
output of forward_propagation
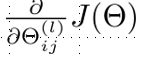
output of back_propagation

output of optimization algorithm
【初次实现用简单的for循环】
【优化算法可以是梯度下降法或其他比较高级的优化算法】
【关于的梯度下降法和之前求导数的梯度法和反向传播算法的关系:梯度法和反向传播算法的作用就是算出梯度下降法步骤中所需要的偏导数,换句话说代价函数的最小化通过优化算法的步骤求解,步骤中的偏导数用梯度法或反向传播算法计算得到。】
参考资料:
1.https://www.bilibili.com/video/BV164411S78V?p=56,B站吴恩达机器学习视频P43-P56




