一维绳波模拟中的探究：完全吸波性边界条件

完全吸波边界条件：

波动方程模拟在计算物理中占有重要的地位，具体应用有声学振动模拟、电磁波模拟、波函数模拟等。这些波动方程（除波函数外）都具有一个大致相同的形式：

\[\frac{\partial^2u}{\partial^2t}=c^2\nabla^2u \]

其中\(u\)为某标量场，\(c\)为声速。
这类方程必定有行波解，在一维情况下，解可以表示为：

\[u(x,t)=u_1(x-ct)+u_2(x+ct) \]

即解可以表示为两列相反传播的行波\(u_1\)、\(u_2\)的叠加。其中\(u_1\)、\(u_2\)为任意一元函数。

这种方程的求解除了与初始条件相关，还与边界有很大关系。边界处一般设置为固定或自由边界条件，两种边界在性质上有些许区别，但又有相似性，例如都能实现完全反射，从而形成驻波。

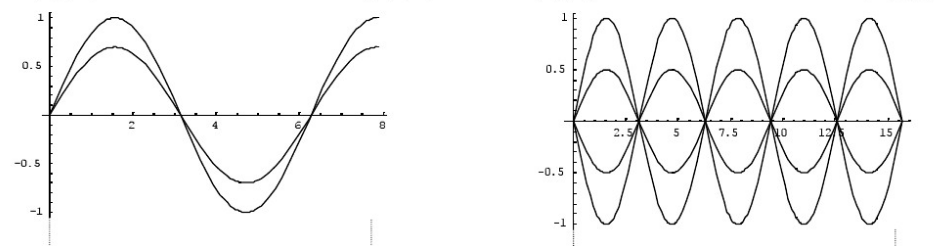
上面两张图为一维绳波的模拟（几个时刻的图形叠在一起）。每张图左端有一个波源，在做正弦振动，而左段为不同的边界条件，导致不同表现。左图为自由式边界条件，绳头可以自由摆动。右图为固定式边界条件，绳头强制固定在0处。

由于波源发出的能量无法被绳头耗散，两种情形下波都会被绳头反射，从而产生驻波。

于是，自然可以想象，会不会有一种边界条件，使右行波完全被吸收，从而不产生任何反射呢？答案是有的。可以想象，假如绳子绳头之外还有绳较长的延伸，从而做到在实验关心的时间之内，右行的波还没有碰到真正的边界，不存在反射，则右行的波就好像被“完全吸收”了。就是说，无限长绳等价于完全吸波条件。

但是电脑永远模拟不了无限，而只能用有限长的绳子近似“完全吸波条件”。因而实验时间不能太长，至少在反射波进入人们关心的区域之前，必须中止模拟，否则“完全吸波条件”失效，模拟会出现很大偏差。

并且即使这样，还是浪费了大量的计算资源在人们不关心的区域的波动方程计算上。这注定是一个糟糕的方法。

存不存在更好的方法？其实是有的。仔细观察模拟的机制，只要对绳头进行人为的操纵，让绳头的行为表现得和无限长绳情况下一模一样，就可以“骗过”左方的绳子，让绳子“以为”右行波还没有碰到边界，从而不会发生反射。

但是该如何认为移动绳头才能让绳头“蒙混过关”呢？天真的想法是利用该问题中只包含右行波的特点：

\[u(x,t)=u_1(x-ct) \]

在该解中，绳子上每一个点的运动状态都滞后重复前面的点的运动状态，即：

\[u(x_1,t)=u(x_1,t-\frac{x_1-x_0}{c}) \]

那么绳头只需要简单地滞后重复某个相邻点的运动，即可完美地实现“完全吸波”。

然而数值模拟残酷地表明，这种方法完全行不通！具体原因和数值离散过程密切相关，笔者能力和精力有限，并没有进一步研究。

幸好，绳波系统有一个十分优异的特性——线性，将绳头视为一个系统，绳头的位移看成系统的输出端，而与绳头相连的倒数第二个节点的位移看成该系统的输入端，则该系统是一个线性时不变系统。该系统的含时响应完全线性取决与输入端的位移方程。

数学推导：

取绳头的位移为\(u_o(t)\)（输出）,而绳头前一个节点的位移为\(u_i(t)\)（输入），则线性时不变系统有如下优良特性：

\[u_o(t)=\int_0^t{f(p)u_i(t-p)dp} \]

又由于：

\[\begin{aligned} u_o(t)&=\int_0^t{u_i(t-p)dF(p)}\\ &=-\int_0^t{F(p)du_i(t-p)}+[u_i(t-p)F(p)]\bigg|^t_0 \end{aligned} \]

式中，\(F(t)=\int^t_0f(t)dt\)，因而最后一项为0。上式最终化简为：

\[u_o(t)=\int_0^t{F(p)\dot{u_i}(t-p)dp} \]

我们把\(F(t)\)叫做绳头的“冲击响应函数”，因为如果输入函数具有以下形式：

\[u_i(t)=\bigg\{ \begin{aligned} 0,t\lt\epsilon\\ 1,t\ge\epsilon\\ \end{aligned} \]

其中\(\epsilon\)为一无限接近0的小量，则输出函数为：

\[\begin{aligned} u_o(t)&=\int_0^t{F(p)\dot{u_i}(t-p-\epsilon)dp}\\ &=\int_0^t{F(p)\delta(t-p-\epsilon)dp}\\ &=F(t-\epsilon)\\ &=F(t) \end{aligned} \]

冲击响应函数反映了当输入函数为阶跃函数时，输出端的变化情况。我们接下来的工作就是找到这个阶跃函数。

在数值模拟中，绳波系统可以离散为有多个节点的一条长链，相邻节点之间用弹簧连接，弹簧施加线性恢复力。对于第\(n\)个节点的位移\(u_n(t)\)，运动学方程如下：

\[\ddot{u_n}(t)=\frac{\Delta x}{2c}\bigg(u_{n-1}(t)-2u_{n}(t)+u_{n+1}(t)\bigg) \]

可以通过设置\(t'=t\)实现无量纲化：

\[\ddot{u_n}(t')=\frac{1}{2}\bigg(u_{n-1}(t')-2u_{n}(t')+u_{n+1}(t')\bigg) \]

绳波模型的离散化示意图：

由于该系统实际上具有无限多个节点力学分析将变得十分棘手。但是，有一种方法可以巧妙破解这一难题，从而实现物理系统的方程化：

考虑倒数第1、2个节点，设它们对左方的冲击响应函数分别为\(F_A(t)\)和\(F_B(t)\)，由于系统右端为无限长序列，则应该有：

\[F_A(t)=F_B(t)=F(t) \]

现在考虑运动方程：

\[\begin{aligned} \ddot{u_A}(t)&=\frac{1}{2}(1-2u_A(t)+u_B(t))\\ u_A(t)&=F(t)\\ u_B(t)&=\int_0^t{F(p)\dot{u_A}(p-t)dp} \end{aligned} \]

联立方程有：

\[\ddot{F(t)}=\frac{1}{2}\bigg(1-2F(t)+\int_0^t{F(p)\dot{F}(p-t)dp}\bigg)\\ \]

其中初值条件为：

\[\begin{aligned} F(t)&=0\\ \dot{F}(t)&=0 \end{aligned} \]

这个方程是一个积分微分混合型方程，并且由于涉及到卷积，难以有效消除积分号，笔者能力有限难以给出解析解。不过该方程可以用皮卡迭代序列给出级数解。经过艰苦卓绝的求解（玄学找规律），笔者得到级数式为：

\[F(x)=\sum^{\infty}_{n=2}{\frac{(-1)^n*2n}{2^n*(n!)^2}*x^{2n-2}} \]

利用Python绘图显示图像：

可见当时间趋于无穷时，系统会逐渐稳定在1附近，这符合绳波冲击响应函数的特点。

注：由于泰勒级数收敛性较差，该级数用double精度计算会在\(x=20\)之后发散。为了正确计算，必须提高计算精度。高精度计算的方法在博文Java 高精度浮点数计算工具中有所介绍。

只要绳头的位移始终满足：

\[u_o(t)=\int_0^t{F(p)\dot{u_i}(t-p)dp} \]

即能做到完全吸收向右传来的波，而避免反射波产生，即“完全吸波边界条件”。

但是，上式还有一个问题，即仍然需要无限大的储空间才能记录所有时刻的\(u_i(t)\)，方法仍然没有可行性。为了解决这一问题，注意到：

\[\lim_{t\to\infty}{F(t)}=1 \]

可以设置截断距离\(L\)，使积分近似为：

\[\begin{aligned} u_o(t)&=\int_0^L{F(p)\dot{u_i}(t-p)dp}+\int_L^t{F(p)\dot{u_i}(t-p)dp}\\ &\approx\int_0^L{F(p)\dot{u_i}(t-p)dp}+\int_L^t{1*\dot{u_i}(t-p)dp}\\ &=\int_0^L{F(p)\dot{u_i}(t-p)dp}+u_i(t-L) \end{aligned} \]

至此，数学推导部分已经全部完成，只剩下程序实现了。

程序模拟：

由于笔者使用java做科学计算的习惯（怪癖），程序由java实现。共编写两个类，一个类进行绳波模拟，另一个专注于计算绳头的冲击响应。以下是模拟结果。

固定式边界条件：

自由式边界条件：

完全吸波边界条件：

可以看出，完全吸收式边界条件较为出色地完成了任务，波包到达边界后几乎没有反弹，就好像边界为无穷大一样。

代码：

见我的github页面，测试代码也在里面。程序代码比较容易理解。

结束语：

通过本文的推导，我们得出了完全吸波边界的一种可行方法，该方法在计算机波动模拟中十分有用，尤其适用于包含无穷大场景，需要排除反射波的情况。不过笔者没有想出来如何在2维以上波动系统中实现类似边界条件。

* 本文为笔者课程学习闲暇时的一点思考，可能有naive的地方。公式推导基本是自己脑洞的，专业性欠缺，如果有误请各位高人指正。