hihocoder #1388 : Periodic Signal fft
题目链接:
https://hihocoder.com/problemset/problem/1388
Periodic Signal
内存限制:256MB
样例输出
80
0
题意
给你两个大小为n的数组a,b,求:
题解
构造下a,b数组就可以转换成多项式乘法问题,然后用fft计算,注意最后计算结果会有浮点误差,但是大小关系还是可以用的,所以求出最大的位置之后,把答案再算一遍。
构造:
另n等于3:
a0a1a2 --> a2a1a0
b0b1b2 --> b0b1b2b0b1b2这样x2到x4的系数就是答案。
代码
#include<algorithm>
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
#define scf scanf
#define prf printf
const int maxn=24e4+10;
const double PI=acos(-1.0);
const double eps=1e-8;
typedef long long LL;
struct Complex {
double real, image;
Complex(double real, double image):real(real),image(image) {}
Complex() {}
friend Complex operator + (const Complex &c1, const Complex &c2) {
return Complex(c1.real + c2.real, c1.image + c2.image);
}
friend Complex operator - (const Complex &c1, const Complex &c2) {
return Complex(c1.real - c2.real, c1.image - c2.image);
}
friend Complex operator * (const Complex &c1, const Complex &c2) {
return Complex(c1.real*c2.real - c1.image*c2.image, c1.real*c2.image + c1.image*c2.real);
}
}A[maxn],B[maxn];
struct IterativeFFT {
Complex A[maxn];
int rev(int id, int len) {
int ret = 0;
for(int i = 0; (1 << i) < len; i++) {
ret <<= 1;
if(id & (1 << i)) ret |= 1;
}
return ret;
}
//当DFT= 1时是DFT, DFT = -1则是逆DFT
//对长度为len(2的幂)的数组进行DFT变换
void FFT(Complex *a,int len, int DFT) {
for(int i = 0; i < len; i++)
A[rev(i, len)] = a[i];
for(int s = 1; (1 << s) <= len; s++) {
int m = (1 << s);
Complex wm = Complex(cos(DFT*2*PI/m), sin(DFT*2*PI/m));
//这一层结点的包含数组元素个数都是(1 << s)
for(int k = 0; k < len; k += m) {
Complex w = Complex(1, 0);
//折半引理, 根据两个子节点计算父亲节点
for(int j = 0; j < (m >> 1); j++) {
Complex t = w*A[k + j + (m >> 1)];
Complex u = A[k + j];
A[k + j] = u + t;
A[k + j + (m >> 1)] = u - t;
w = w*wm;
}
}
}
if(DFT == -1) for(int i = 0; i < len; i++) A[i].real /= len, A[i].image /= len;
for(int i=0; i<len; i++) a[i]=A[i];
}
int solve(Complex* a,Complex* b,int len,int n){
FFT(a,len,1),FFT(b,len,1);
for(int i=0;i<len;i++) a[i]=a[i]*b[i];
FFT(a,len,-1);
int pos=0;
double ans=-1;
for(int i=0;i<n;i++){
if(ans+eps<a[i+n-1].real){
ans=a[i+n-1].real;
pos=i;
}
}
return pos;
}
} myfft;
LL a[maxn],b[maxn];
int n;
int main(){
int tc;
scf("%d",&tc);
while(tc--){
scf("%d",&n);
int len=1; while(len<n*2) len<<=1;
for(int i=0;i<n;i++) scf("%lld",&a[i]);
for(int i=0;i<n;i++) scf("%lld",&b[i]);
for(int i=0;i<len;i++){
A[i]=Complex(0,0),B[i]=Complex(0,0);
}
for(int i=0;i<n;i++){
A[i]=Complex(a[n-1-i],0),B[i]=Complex(b[i],0);
A[i+n]=Complex(0,0), B[i+n]=Complex(b[i],0);
}
int k=myfft.solve(A,B,len,n);
LL ans=0;
for(int i=0;i<n;i++){
int j=(i+k)%n;
ans+=(a[i]-b[j])*(a[i]-b[j]);
}
prf("%lld\n",ans);
}
}

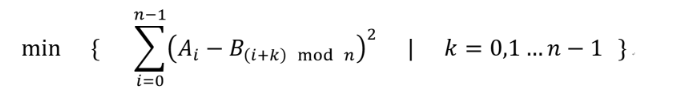

 浙公网安备 33010602011771号
浙公网安备 33010602011771号