最长公共子串和最长公共子序列

1.两个字符串的最长公共子串与最长公共子序列的区别：

最长公共子串要求在原字符串中是连续的，而子序列只需要保持相对顺序一致，并不要求连续。

下面分别讲讲怎么求它们。

 

2.最长公共子串：

（1）暴力解法：

要求最长公共子串，可以用暴力的解法：

int longestSubstring(string x, string y) {
    int max = 0;
    string str = "";
    for (int i = 0; i < x.size(); i++) {
        int len = 0;
        int j = i;
        while (j < x.size()) {
            str += x[j];
            if (y.find(str) == y.npos) break;
            len++;
            j++;
            if (len > max) max = len;
        }
        str = "";
    }
    return max;   
}

或者：

int longestSubstring(string x, string y) {
    int xlen = x.size();
    int ylen = y.size();
    if (xlen == 0 || ylen == 0) {
        return 0;   
    }
    int max = -1;
    for (int i = 0; i < xlen; i++) {
        for (int j = 0; j < ylen; j++) {
            int m = i, n = j;
            int len = 0;
            while (m < xlen && n < ylen) {
                if (x[m] != y[n]) {
                    break;
                }
                m++;
                n++;
                len++;
            }
            if (len > max) {
                max = len;
            }
        }
    }
    return max;
}

这种暴力解法唯一值得学习的地方，就是怎么求一个字符串的所有子字符串。用一个二层循环即可，外面一层循环从字符串的头遍历到尾，里面的循环就从当前的位置开始，每个字符地加，这样就可以得到所有的子字符串了。

 

（2）动态规划：

状态转移方程：

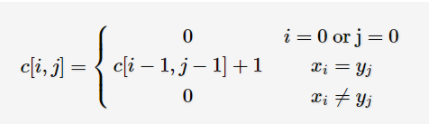
最长公共子串长度就为max{c[i][j]}了，代码如下：

int longestSubstring(string x, string y) {
   vector<vector<int> > f(x.size() + 1, vector<int>(y.size() + 1, 0));
   int max = -1;
   for (int i = 1; i <= x.size(); i++) {
       for (int j = 1; j <= y.size(); j++) {
           if (x[i - 1] != y[j - 1]) f[i][j] = 0;
           else if (x[i - 1] == y[j - 1]) f[i][j] = f[i - 1][j - 1] + 1;
           if (max < f[i][j]) {
             max = f[i][j];
           }
       }
    }
    return max;
}

 

（3）后缀数组解法

有这么一个解法，但我没有看过。

 

 

3.最长公共子序列

直接用动态规划解决，转移方程为：

 

 代码：

int longestSubstring(string x, string y) {
    int **dp = new int*[x.size() + 1];
    for (int i = 0; i < x.size(); i++) {
        dp[i] = new int[y.size() + 1];
    }
    for (int i = 0; i <= x.size(); i++) dp[i][0] = 0;
    for (int i = 0; i <= y.size(); i++) dp[0][i] = 0;
    for (int i = 1; i <= x.size(); i++) {
        for (int j = 1; j <= y.size(); j++) {
            if (x[i] == y[j]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            }
            else {
                dp[i][j] = dp[i - 1][j] > dp[i][j - 1] ? dp[i - 1][j] : dp[i][j - 1];
            }
        }
    }
    return dp[x.size()][y.size()];
}