拉格朗日插值
一,介绍
学过FFT的人都应该知道什么叫做插值,插值的意思就是说将一个多项式从点值表达转变成系数表达。
在FFT的插值中为什么可以做到n log n,是因为单位复数根的关系。
那对于普通的插值应该怎么办呢?解方程是一种方法,但是这个在计算机中十分不现实。
所以有许多种插值的方法,其中比较普及的就是拉格朗日插值。
二,定义
对某个多项式函数,已知有给定的k + 1个取值点:
其中 对应着自变量的位置,而
对应着自变量的位置,而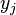 对应着函数在这个位置的取值。
对应着函数在这个位置的取值。
假设任意两个不同的xj都互不相同,那么应用拉格朗日插值公式所得到的拉格朗日插值多项式为:
其中每个 为拉格朗日基本多项式(或称插值基函数),其表达式为:
为拉格朗日基本多项式(或称插值基函数),其表达式为:
拉格朗日基本多项式 的特点是在
的特点是在 上取值为1,在其它的点
上取值为1,在其它的点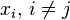 上取值为0。
上取值为0。
三,例子
假设有某个二次多项式函数 ,已知它在三个点上的取值为:
,已知它在三个点上的取值为:

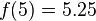
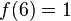
要求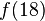 的值。
的值。
首先写出每个拉格朗日基本多项式:
然后应用拉格朗日插值法,就可以得到 的表达式(
的表达式( 为函数
为函数 的插值函数):
的插值函数):
此时代入数值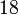 就可以求出所需之值:
就可以求出所需之值: 。
。
四,证明唯一性
就是说n+1个点对应的n次多项式只有一个,这个需要证明,但是一般都会直接当成结论,所以不需要去记忆。
五,优点和缺点
拉格朗日插值法的公式结构整齐紧凑,在理论分析中十分方便,然而在计算中,当插值点增加或减少一个时,所对应的基本多项式就需要全部重新计算,
于是整个公式都会变化,非常繁琐[5]。这时可以用重心拉格朗日插值法或牛顿插值法来代替。此外,当插值点比较多的时候,拉格朗日插值多项式的次数
可能会很高,因此具有数值不稳定的特点,也就是说尽管在已知的几个点取到给定的数值,但在附近却会和“实际上”的值之间有很大的偏差(如右下图)[6]。
这类现象也被称为龙格现象,解决的办法是分段用较低次数的插值多项式。



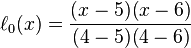
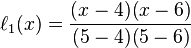

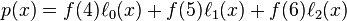
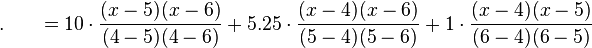
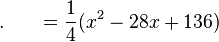



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· DeepSeek 解答了困扰我五年的技术问题
· 为什么说在企业级应用开发中,后端往往是效率杀手?
· 用 C# 插值字符串处理器写一个 sscanf
· Java 中堆内存和栈内存上的数据分布和特点
· 开发中对象命名的一点思考
· 为什么说在企业级应用开发中,后端往往是效率杀手?
· DeepSeek 解答了困扰我五年的技术问题。时代确实变了!
· 本地部署DeepSeek后,没有好看的交互界面怎么行!
· 趁着过年的时候手搓了一个低代码框架
· 推荐一个DeepSeek 大模型的免费 API 项目!兼容OpenAI接口!