bzoj3561 莫比乌斯反演

DZY Loves Math VI

Time Limit: 10 Sec  Memory Limit: 256 MB
Submit: 518  Solved: 344
[Submit][Status][Discuss]

Description

给定正整数n,m。求
 
 

Input

一行两个整数n,m。

Output

一个整数，为答案模1000000007后的值。

Sample Input

5 4

Sample Output

424

HINT

 

数据规模：

1<=n,m<=500000，共有3组数据。

 

Source

 

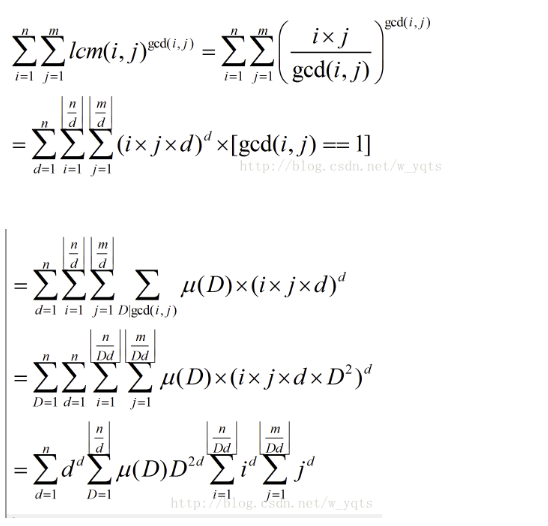
 1 #pragma GCC optimize(2)
 2 #pragma G++ optimize(2)
 3 #include<iostream>
 4 #include<algorithm>
 5 #include<cmath>
 6 #include<cstdio>
 7 #include<cstring>
 8 
 9 #define ll long long
10 #define inf 1000000000
11 #define mod 1000000007
12 #define N 500007
13 using namespace std;
14 inline int read()
15 {
16     int x=0,f=1;char ch=getchar();
17     while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
18     while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
19     return x*f;
20 }
21 
22 int n,m,ans,tot;
23 int miu[N],p[N];
24 int a[N],sum[N];
25 bool flag[N];
26 
27 void prepration()
28 {
29     miu[1]=1;
30     for (int i=2;i<=n;i++)
31     {
32         if (!flag[i]){p[++tot]=i;miu[i]=-1;}
33         for (int j=1;j<=tot&&p[j]*i<=n;j++)
34         {
35             flag[i*p[j]]=1;miu[i*p[j]]=-miu[i];
36             if (i%p[j]==0){miu[i*p[j]]=0;break;}
37         }
38     }
39 }
40 inline int mul(int x,int y)
41 {
42     if (y==1) return x;
43     int t=mul(x,y>>1);
44     t=(ll)t*t%mod;
45     if (y&1) t=(ll)t*x%mod;
46     return t;
47 }
48 int main()
49 {
50     n=read();m=read();if (n<m) swap(n,m);
51     prepration();
52     for (int i=1;i<=n;i++) a[i]=1;
53     for (int d=1;d<=m;d++)
54     {
55         int x=mul(d,d),y=0;
56         for (int i=1;i<=n/d;i++)
57         {
58             a[i]=(ll)a[i]*i%mod;sum[i]=(sum[i-1]+a[i])%mod;
59         }
60         for (int D=1;D<=n/d;D++)if (miu[D])
61         {
62             int t=mul(D,2*d);
63             y=(y+(ll)t*miu[D]%mod*sum[n/d/D]%mod*sum[m/d/D]%mod)%mod;
64         }
65         ans=(ans+(ll)x*y%mod)%mod;
66     }
67     printf("%d",ans);
68 }

 

posted @ 2018-03-08 21:18  Kaiser-  阅读(230)  评论(0)  编辑  收藏  举报