bzoj 3309 DZY Loves Math 莫比乌斯反演

DZY Loves Math

Time Limit: 20 Sec  Memory Limit: 512 MB
Submit: 1303  Solved: 819
[Submit][Status][Discuss]

Description

对于正整数n，定义f(n)为n所含质因子的最大幂指数。例如f(1960)=f(2^3 * 5^1 * 7^2)=3, f(10007)=1, f(1)=0。
给定正整数a,b，求sigma(sigma(f(gcd(i,j)))) (i=1..a, j=1..b)。

 

Input

第一行一个数T，表示询问数。
接下来T行，每行两个数a,b，表示一个询问。

 

Output

对于每一个询问，输出一行一个非负整数作为回答。

 

Sample Input

4
7558588 9653114
6514903 4451211
7425644 1189442
6335198 4957

Sample Output

35793453939901
14225956593420
4332838845846
15400094813

HINT

 

【数据规模】

T<=10000

 

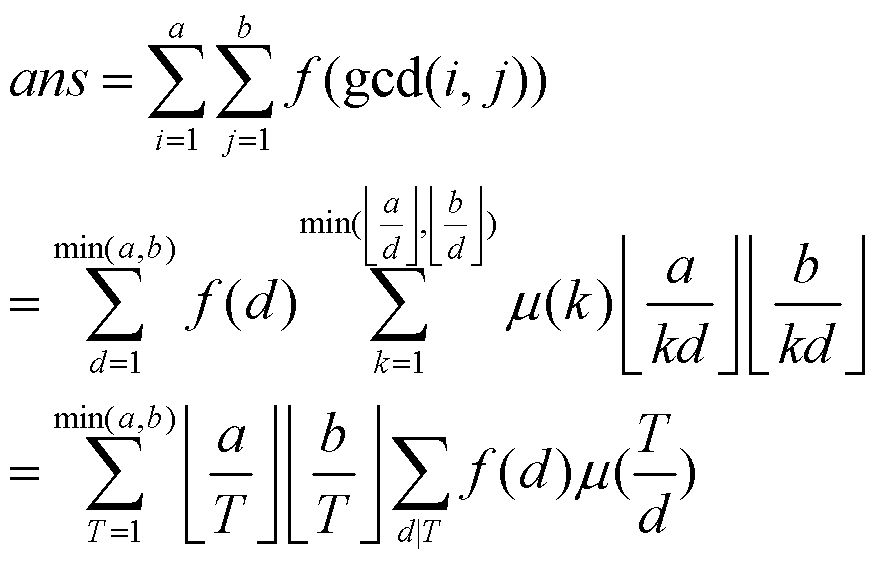
 1 #pragma GCC optimize(2)
 2 #pragma G++ optimzie(2)
 3 #include<cstring>
 4 #include<cmath>
 5 #include<cstdio>
 6 #include<algorithm>
 7 #include<iostream>
 8 
 9 #define N 10000007
10 #define ll long long
11 using namespace std;
12 inline int read()
13 {
14     int x=0,f=1;char ch=getchar();
15     while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
16     while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
17     return x*f;
18 }
19 
20 int n,m;
21 int pri[N],tot;
22 int t[N],last[N],g[N];
23 bool flag[N];
24 
25 void init()
26 {
27     for (int i=2;i<N;i++)
28     {
29         if(!flag[i])
30         {
31             pri[++tot]=i;
32             last[i]=t[i]=g[i]=1;
33         }
34         for(int j=1;pri[j]*i<N&&j<=tot;j++)
35         {
36             int x=i*pri[j];flag[x]=true;
37             if(i%pri[j]==0)
38             {
39                 last[x]=last[i];
40                 t[x]=t[i]+1;
41                 if(last[x]==1)g[x]=1;
42                 else g[x]=(t[last[x]]==t[x]?-g[last[x]]:0);
43                 break;
44             }
45             else
46             {
47                 last[x]=i;
48                 t[x]=1;
49                 g[x]=(t[i]==1?-g[i]:0);
50             }
51         }
52     }
53     for (int i=1;i<N;i++)g[i]+=g[i-1];
54 /*    for (int i=11;i<=20;i++)
55         cout<<"xzpxzpxzpxzpxzpxzp==laji="<<g[i]<<endl;*/
56 }
57 ll solve(int n,int m)
58 {
59     if(n>m)swap(n,m);ll res=0;
60     for (int i=1,last;i<=n;i=last+1)
61     {
62         last=min(n/(n/i),m/(m/i));
63         res+=1ll*(n/i)*(m/i)*(g[last]-g[i-1]);
64     }
65     return res;
66 }
67 int main()
68 {
69     init();
70     int T=read();
71     while(T--)
72     {
73         n=read(),m=read();
74         printf("%lld\n",solve(n,m));
75     }
76 }

 

 

posted @ 2018-03-08 21:02  Kaiser-  阅读(175)  评论(0)  编辑  收藏  举报