bzoj 3111 蚂蚁 动态规划
题目描述
在一个 n*m 的棋盘上,每个格子有一个权值,初始时,在某个格子的顶点处一只面朝北的蚂蚁,我们只知道它的行走路线是如何转弯,却不知道每次转弯前走了多长。
蚂蚁转弯是有一定特点的,即它的转弯序列一定是如下的形式:右转,右转,左转,左转,右转,右转…左转,左转,右转,右转,右转。即两次右转和两次左转交替出现的形式,最后两次右转(最后两次一定是右转)后再多加一次右转。我们还知道,蚂蚁不会在同一个位置连续旋转两次,并且蚂蚁行走的路径除了起点以外,不会到达同一个点多次,它最后一定是回到起点然后结束自己的行程,而且蚂蚁只会在棋盘格子的顶点处转弯。
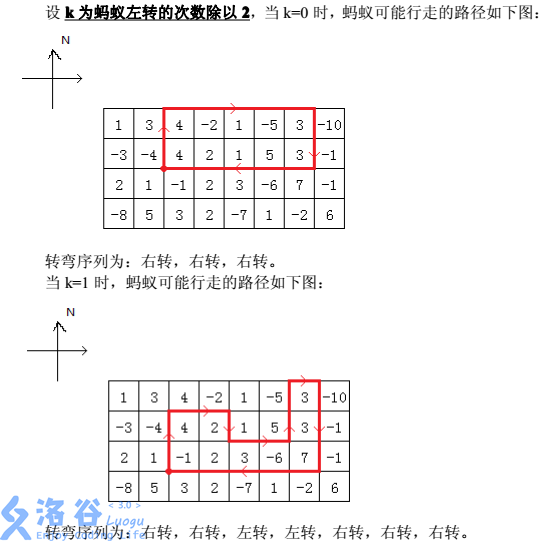
现在已知棋盘大小、每个格子的权值以及左转次数/2 的值,问蚂蚁走出的路径围出的封闭图形,权值之和最大可能是多少。
输入输出格式
输入格式:
在输入文件ant.in 中,第一行三个数n,m,k。意义如题目描述。
接下来一个n 行m 列的整数矩阵,表示棋盘。
输出格式:
一个数,表示蚂蚁所走路径围出的图形可能的最大权值和。
输入输出样例
说明
【样例说明】
除了第一行的第二个和第一行的第四个都要围起来才至少合法。
【数据规模与约定】
10%的数据所有格子中权值均非负
另20%的数据n=2
另30%的数据k=0
100%的数据1≤n≤100,1≤m≤100,0≤k≤10 保证存在合法路径,数据有梯度,格子中每个元素的值绝对值不超过 10000
P3335 这个题思维难度还是有的。。(至少我是这么想的。。大佬就别吐槽我了)
首先,通过题目描述,我们可以在纸上画一画,可以发现,图像一定是像长城一样的
就是好多个矩形它们的底在一条直线上,高和宽不同,而且,还有一点就是它是高低相间的
而且由右转形成高峰,由左转形成低谷。
那么我们可以枚举图的右下角(i,j),那么有两种情况:
一:第j-1列和第j列在同一个矩形里;
二:第j-1列和第j列在不同的矩形里;
我们要记录的状态与点(i,j),p(指的是当前枚举的是第p个矩形),h(当前枚举的举行高度为i-h+1)有关
所以用f[i][j][p][h]来记录‘一’情况的状态,用g[i][j][p][h][0/1]来记录‘二’情况的状态
这里0表示上一个矩形高度高于h,1表示低于h;
那么转移就好写了:
f[i][j][p][h]=max(f[i][j-1][p][h],g[i][j-1][p-1][h][p%2])+s[i][j]-s[h-1][j];
对了,这里这个s数组求的是每一列的前缀和,可以在输入中预处理出来,方便计算用;
关于g数组的维护,我们已经维护出f数组的第j列了
那么这一列所在的矩形要么是低谷,要么是高峰,我们都要考虑
->高峰:
g[i][j][p][h][0]=max(f[i][j][p][h-1],g[i][j][p][h-1][0]);
->低谷:
g[i][j][p][h][1]=max(f[i][j][p][h+1],g[i][j][p][h+1][1]);
当然我们可以在计算过程中更新答案,还可以省掉i这一维
因为从方程中就可以看出来i其实没有参与转移
1 #pragma GCC optimize(2) 2 #pragma G++ optimize(2) 3 #pragma GCC target ("avx") 4 #include<iostream> 5 #include<algorithm> 6 #include<cmath> 7 #include<cstdio> 8 #include<cstring> 9 using namespace std; 10 const int maxn=120; 11 const int Inf=1000000001; 12 int n,m,k,ans; 13 int a[maxn][maxn]; 14 int f[maxn][25][maxn]; 15 int g[maxn][25][maxn][2]; 16 int s[maxn][maxn]; 17 void ini() 18 { 19 scanf("%d%d%d",&n,&m,&k); 20 //因为有2*k次左转,所以总矩形数就是k*2+1 21 k=k*2+1; 22 for(int i=1;i<=n;i++) 23 { 24 for(int j=1;j<=m;j++) 25 { 26 scanf("%d",&a[i][j]); 27 s[i][j]=s[i-1][j]+a[i][j]; 28 } 29 } 30 //预处理 因为要求最大值,所以边界赋值为-Inf; 31 for(int p=1;p<=k;p++) 32 { 33 for(int h=1;h<=n;h++) 34 { 35 f[0][p][h]=-Inf; 36 g[0][p][h][0]=-Inf; 37 g[0][p][h][1]=-Inf; 38 } 39 } 40 } 41 void dp() 42 { 43 ans=-Inf; 44 for(int i=1;i<=n;i++) 45 { 46 for(int j=1;j<=m;j++) 47 { 48 for(int p=1;p<=k;p++) 49 { 50 for(int h=i;h>=1;h--)//维护f数组 51 { 52 f[j][p][h]=max(f[j-1][p][h],g[j-1][p-1][h][p%2])+s[i][j]-s[h-1][j]; 53 } 54 //维护g数组 55 g[j][p][1][0]=-Inf; 56 //0指当前矩形比下一个高,所以从高到低更新,才可以确保取最大值的矩形一定是高的 57 for(int h=2;h<=i;h++) 58 { 59 g[j][p][h][0]=max(f[j][p][h-1],g[j][p][h-1][0]); 60 } 61 g[j][p][i][1]=-Inf; 62 //1指当前矩形比下一个底,所以从低到高更新,才可以确保取最大值的矩形一定是低的 63 for(int h=i-1;h>=1;h--) 64 { 65 g[j][p][h][1]=max(f[j][p][h+1],g[j][p][h+1][1]); 66 } 67 } 68 //更新答案,因为最后一列一定是高的,所以用0转移; 69 ans=max(ans,max(f[j][k][i],g[j][k][i][0])); 70 } 71 } 72 } 73 int main() 74 { 75 ini();//读入一些数据 76 dp(); 77 printf("%d\n",ans); 78 return 0; 79 }




