bzoj3514 Codechef MARCH14 GERALD07加强版 lct预处理+主席树
Codechef MARCH14 GERALD07加强版
Time Limit: 60 Sec Memory Limit: 256 MBSubmit: 1951 Solved: 746
[Submit][Status][Discuss]
Description
N个点M条边的无向图,询问保留图中编号在[l,r]的边的时候图中的联通块个数。
Input
第一行四个整数N、M、K、type,代表点数、边数、询问数以及询问是否加密。
接下来M行,代表图中的每条边。
接下来K行,每行两个整数L、R代表一组询问。对于type=0的测试点,读入的L和R即为询问的L、R;对于type=1的测试点,每组询问的L、R应为L xor lastans和R xor lastans。
Output
K行每行一个整数代表该组询问的联通块个数。
Sample Input
3 5 4 0
1 3
1 2
2 1
3 2
2 2
2 3
1 5
5 5
1 2
1 3
1 2
2 1
3 2
2 2
2 3
1 5
5 5
1 2
Sample Output
2
1
3
1
1
3
1
HINT
对于100%的数据,1≤N、M、K≤200,000。
2016.2.26提高时限至60s
Source
题解:
首先把边依次加到图中,若当前这条边与图中的边形成了环,那么把这个环中最早加进来的边弹出去
并将每条边把哪条边弹了出去记录下来:ntr[i] = j,特别地,要是没有弹出边,ntr[i] = 0;
这个显然是可以用LCT来弄的对吧。
然后对于每个询问,我们的答案就是对l~r中ntr小于l的边求和,并用n减去这个值
正确性可以YY一下:
如果一条边的ntr >= l,那么显然他可以与从l ~ r中的边形成环,那么它对答案没有贡献
反之如果一条边的ntr < l那么它与从l ~ r中的边是不能形成环的,那么他对答案的贡献为-1
对于查询从l ~ r中有多少边的ntr小于l。
函数式线段树询问即可
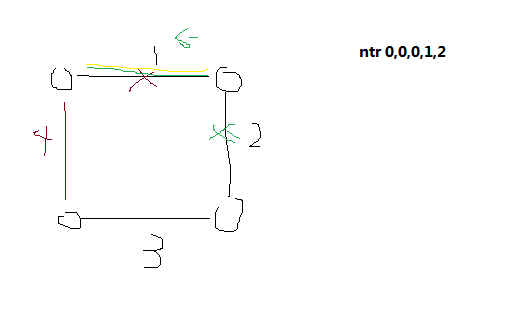
比如这个图,如果询问2-5那么,对于5这条边来说,是没意义的,因为5只能将
2这条边的效果去掉,因为2最早,所以不能算,
因此ans=4-3=1而不是4-4=0
函数式线段树记录什么呢,就是rt[i]表示i为右端点,
然后左端点的话就是维护前缀和的形式即可。
1 #include<cstring> 2 #include<cmath> 3 #include<iostream> 4 #include<algorithm> 5 #include<cstdio> 6 7 #define inf 1000000000 8 #define ll long long 9 #define N 400005 10 #define M 200005 11 #define NUM 4000007 12 using namespace std; 13 inline int read() 14 { 15 int x=0,f=1;char ch=getchar(); 16 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 17 while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} 18 return x*f; 19 } 20 21 int n,m,q,ans,tot,sz,flag; 22 int s[N],st[M],root[M]; 23 int c[N][2],fa[N],val[N],mn[N],sum[NUM],ls[NUM],rs[NUM],rev[N]; 24 struct Node 25 { 26 int u,v; 27 }e[M]; 28 29 inline bool isroot(int x){return c[fa[x]][0]!=x&&c[fa[x]][1]!=x;} 30 void update(int p) 31 { 32 int l=c[p][0],r=c[p][1];mn[p]=p; 33 if(val[mn[l]]<val[mn[p]])mn[p]=mn[l]; 34 if(val[mn[r]]<val[mn[p]])mn[p]=mn[r]; 35 } 36 void pushdown(int x) 37 { 38 int l=c[x][0],r=c[x][1]; 39 if(rev[x]) 40 { 41 rev[x]^=1;rev[l]^=1;rev[r]^=1; 42 swap(c[x][0],c[x][1]); 43 } 44 } 45 void rotate(int x) 46 { 47 int y=fa[x],z=fa[y],l,r; 48 if(c[y][0]==x)l=0;else l=1;r=l^1; 49 if(!isroot(y)) 50 { 51 if(c[z][0]==y)c[z][0]=x;else c[z][1]=x; 52 } 53 fa[y]=x,fa[x]=z,fa[c[x][r]]=y; 54 c[y][l]=c[x][r],c[x][r]=y; 55 update(y),update(x); 56 } 57 void splay(int x) 58 { 59 int top=0;s[++top]=x; 60 for(int i=x;!isroot(i);i=fa[i])s[++top]=fa[i]; 61 for(int i=top;i;i--)pushdown(s[i]); 62 while(!isroot(x)) 63 { 64 int y=fa[x],z=fa[y]; 65 if(!isroot(y)) 66 { 67 if(c[y][0]==x^c[z][0]==y)rotate(x); 68 else rotate(y); 69 } 70 rotate(x); 71 } 72 update(x); 73 } 74 void access(int x) 75 { 76 for(int t=0;x!=0;t=x,x=fa[x]) 77 splay(x),c[x][1]=t,update(x); 78 } 79 void makeroot(int x) 80 { 81 access(x); 82 splay(x); 83 rev[x]^=1; 84 } 85 void link(int x,int y) 86 { 87 makeroot(x); 88 fa[x]=y; 89 } 90 void cut(int x,int y) 91 { 92 makeroot(x),access(y),splay(y); 93 c[y][0]=fa[x]=0; 94 } 95 int find(int x) 96 { 97 access(x),splay(x); 98 while(c[x][0]) 99 x=c[x][0]; 100 return x; 101 } 102 int query(int x,int y) 103 { 104 makeroot(x); 105 access(y); 106 splay(y); 107 return mn[y]; 108 } 109 void ins(int l,int r,int x,int &y,int val) 110 { 111 y=++sz,sum[y]=sum[x]+1; 112 if(l==r)return; 113 ls[y]=ls[x];rs[y]=rs[x]; 114 int mid=(l+r)>>1; 115 if(val<=mid)ins(l,mid,ls[x],ls[y],val); 116 else ins(mid+1,r,rs[x],rs[y],val); 117 } 118 int query(int l,int r,int x,int y,int val) 119 { 120 if(r==val)return sum[y]-sum[x]; 121 int mid=(l+r)>>1; 122 if(val<=mid)return query(l,mid,ls[x],ls[y],val); 123 else return sum[ls[y]]-sum[ls[x]]+query(mid+1,r,rs[x],rs[y],val); 124 } 125 void init() 126 { 127 tot=n; 128 for(int i=1;i<=m;i++) 129 { 130 int u=e[i].u,v=e[i].v; 131 if(u==v){st[i]=i;continue;} 132 if(find(u)==find(v)) 133 { 134 int t=query(u,v),x=val[t]; 135 st[i]=x; 136 cut(e[x].u,t);cut(e[x].v,t); 137 } 138 tot++,mn[tot]=tot,val[tot]=i; 139 link(u,tot),link(v,tot); 140 } 141 for(int i=1;i<=m;i++) 142 ins(0,m,root[i-1],root[i],st[i]); 143 } 144 int main() 145 { 146 n=read(),m=read(),q=read(),flag=read(); 147 val[0]=inf; 148 for(int i=1;i<=n;i++) mn[i]=i,val[i]=inf; 149 for(int i=1;i<=m;i++) e[i].u=read(),e[i].v=read(); 150 151 init(); 152 153 for(int i=1;i<=q;i++) 154 { 155 int l=read(),r=read(); 156 if(flag)l^=ans,r^=ans; 157 ans=n-query(0,m,root[l-1],root[r],l-1); 158 printf("%d\n",ans); 159 } 160 }



