【bzoj2115】[Wc2011] Xor
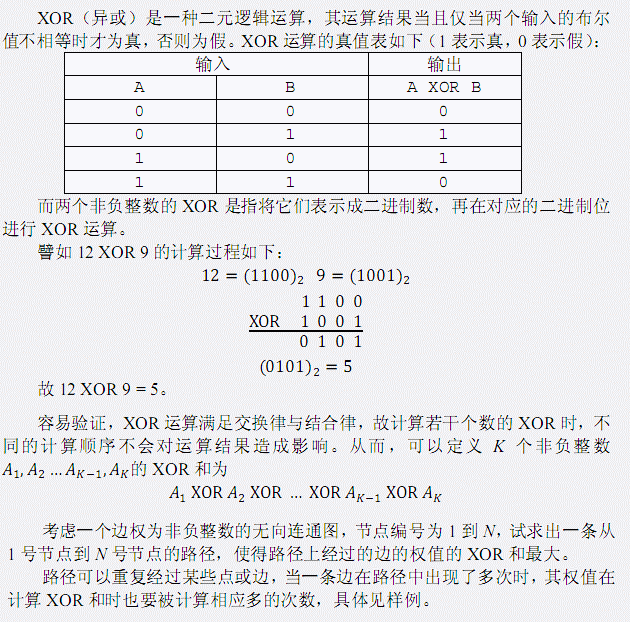
第一行包含两个整数N和 M, 表示该无向图中点的数目与边的数目。 接下来M 行描述 M 条边,每行三个整数Si,Ti ,Di,表示 Si 与Ti之间存在 一条权值为 Di的无向边。 图中可能有重边或自环。
Output
仅包含一个整数,表示最大的XOR和(十进制结果),注意输出后加换行回车。
Sample Input
5 7 1 2 2 1 3 2 2 4 1 2 5 1 4 5 3 5 3 4 4 3 2
Sample Output
6
Hint
正解:dfs+线性基
解题报告:
继续刷线性基...
这道题要求从1到n的最大xor和路径,存在重边,允许经过重复点、重复边。那么在图上作图尝试之后就会发现,路径一定是由许多的环和一条从1到n的路径组成。容易发现,来回走是没有任何意义的,因为来回走意味着抵消。考虑这道题求得是路径xor和最大,所以必然我们要想办法处理环的情况。我的做法是任意地先找出一条从1到n的路径,把这条路径上的xor和作为ans初值(先不管为什么可行),然后我们的任务就变成了求若干个环与这个ans初值所能组合成的xor最大值。显然,我们需要预处理出图上所有的环,并处理出所有环的环上xor值,这当然是dfs寻找,到n的路径的时候顺便求一下就可以了。
当我们得到了若干个环的xor值之后,因为是要求xor最大值,我们就可以构出这所有xor值的线性基。构出之后,再用ans在线性基上取max就可以了。
现在我们来讨论上述做法的可行性。
第一种情况:我们对最终答案产生贡献的某个环离1到n的主路径很远,这样的话,因为至少可以保证1可以到达这个环,那么我们可以走到这个环之后绕环一周之后原路返回,这样从1走到环的路上这一段被重复经过所以无效,但是环上的xor值被我们得到了,所以我们并不关心这个环和主路径的关系,我们只关心环的权值。
第二种情况:我们任意选取的到n的路径是否能保证最优性。假设存在一条更优的路径从1到n,那么这条路径与我们原来的路径构成了一个环,也就会被纳入线性基中,也会被计算贡献,假如这个环会被经过,那么最后的情况相当于是走了两遍原来选取的路径,抵消之后走了一次这个最优路径,所以我们无论选取的是哪条路径作为ans初值,都可以通过与更优情况构成环,然后得到一样的结果。这一证明可以拓展到路径上的任意点的路径选取。
这样我们就可以完美解决了。我第一次WA了一发,因为我没有考虑到ans初值不为0,在线性基上取到xor的max的时候,不能单纯以ans这一位是否为0来决定是否异或上基的这一位,必须要看异或之后取一个max做一个判断才行。
人家题解写得太好,由衷感谢。
1 #include<cstring> 2 #include<cmath> 3 #include<iostream> 4 #include<algorithm> 5 #include<cstdio> 6 #define ll long long 7 using namespace std; 8 9 int n,m; 10 int top;ll num[1000007]; 11 int cnt,head[50007],next[200007],rea[200007];ll val[200007]; 12 ll dis[50007],ans,b[67]; 13 bool vis[50007]; 14 15 void add(int u,int v,ll fee) 16 { 17 next[++cnt]=head[u]; 18 head[u]=cnt; 19 rea[cnt]=v; 20 val[cnt]=fee; 21 } 22 void dfs(int u) 23 { 24 vis[u]=1; 25 for (int i=head[u];i!=-1;i=next[i]) 26 { 27 int v=rea[i];ll fee=val[i]; 28 if (!vis[v]) 29 { 30 dis[v]=dis[u]^fee; 31 dfs(v); 32 } 33 else 34 { 35 num[++top]=dis[u]^dis[v]^fee; 36 top-=(!num[top]); 37 } 38 } 39 } 40 int main() 41 { 42 memset(head,-1,sizeof(head)); 43 scanf("%d%d",&n,&m); 44 int x,y;ll z; 45 for (int i=1;i<=m;i++) 46 { 47 scanf("%d%d%lld",&x,&y,&z); 48 add(x,y,z),add(y,x,z); 49 } 50 dfs(1); 51 for (int i=1;i<=top;i++) 52 for (int j=63;j>=0;j--) 53 if (num[i]>>j&1) 54 if (!b[j]) 55 { 56 b[j]=num[i]; 57 break; 58 } 59 else num[i]^=b[j]; 60 ans=dis[n]; 61 for (int i=63;i>=0;i--) 62 if (!(ans>>i&1)) ans^=b[i]; 63 printf("%lld\n",ans); 64 }



