Bzoj2007 [Noi2010]海拔(平面图最短路)
2007: [Noi2010]海拔
Time Limit: 20 Sec Memory Limit: 552 MBSubmit: 2742 Solved: 1318
[Submit][Status][Discuss]
Description
YT市是一个规划良好的城市,城市被东西向和南北向的主干道划分为n×n个区域。简单起见,可以将YT市看作一个
正方形,每一个区域也可看作一个正方形。从而,YT城市中包括(n+1)×(n+1)个交叉路口和2n×(n+1)条双向道路
(简称道路),每条双向道路连接主干道上两个相邻的交叉路口。下图为一张YT市的地图(n = 2),城市被划分为2
×2个区域,包括3×3个交叉路口和12条双向道路。 小Z作为该市的市长,他根据统计信息得到了每天上班高峰期
间YT市每条道路两个方向的人流量,即在高峰期间沿着该方向通过这条道路的人数。每一个交叉路口都有不同的海
拔高度值,YT市市民认为爬坡是一件非常累的事情,每向上爬h的高度,就需要消耗h的体力。如果是下坡的话,则
不需要耗费体力。因此如果一段道路的终点海拔减去起点海拔的值为h(注意h可能是负数),那么一个人经过这段路
所消耗的体力是max{0, h}(这里max{a, b}表示取a, b两个值中的较大值)。 小Z还测量得到这个城市西北角的交
叉路口海拔为0,东南角的交叉路口海拔为1(如上图所示),但其它交叉路口的海拔高度都无法得知。小Z想知道在
最理想的情况下(即你可以任意假设其他路口的海拔高度),每天上班高峰期间所有人爬坡所消耗的总体力和的最
小值。
Input
第一行包含一个整数n,含义如上文所示。接下来4n(n + 1)行,每行包含一个非负整数分别表示每一条道路每一个
方向的人流量信息。输入顺序:n(n + 1)个数表示所有从西到东方向的人流量,然后n(n + 1)个数表示所有从北到
南方向的人流量,n(n + 1)个数表示所有从东到西方向的人流量,最后是n(n + 1)个数表示所有从南到北方向的人
流量。对于每一个方向,输入顺序按照起点由北向南,若南北方向相同时由西到东的顺序给出(参见样例输入)。
Output
仅包含一个数,表示在最理想情况下每天上班高峰期间所有人爬坡所消耗的总体力和(即总体力和的最小值),结
果四舍五入到整数。
Sample Input
1
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
Sample Output
3
【样例说明】
样例数据见下图。
最理想情况下所有点的海拔如上图所示。
对于100%的数据:1 ≤ n ≤ 500,0 ≤ 流量 ≤ 1,000,000且所有流量均为整数。
【样例说明】
样例数据见下图。
最理想情况下所有点的海拔如上图所示。
对于100%的数据:1 ≤ n ≤ 500,0 ≤ 流量 ≤ 1,000,000且所有流量均为整数。
题解:
显然我们只需要考虑0和1的分界线在何处即可。当然我们需要找到一些边集,把图分成两半,且权值和最小。这不就是最小割吗...所以直接把原图转成对偶图,然后跑dijkstra。
注意连边的时候考虑方向,我们不妨假定对偶图边经过的方向,左边海拔为0,右边海拔为1,然后只要算0到1的,所以就是正方向的权值。所以我们只需要把方向相反的两条边在对偶图中也构出方向相反的即可。
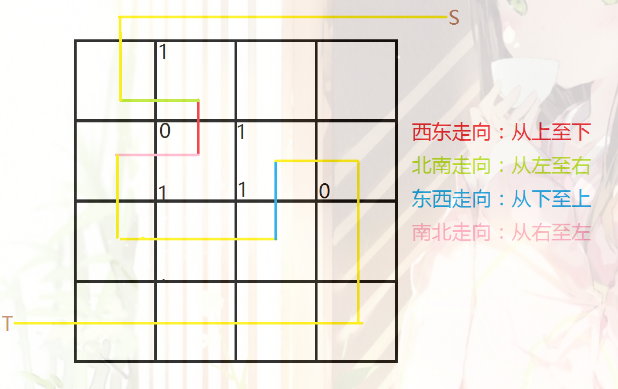
这样就可以了。
1 #include<algorithm> 2 #include<iostream> 3 #include<cstring> 4 #include<cstdio> 5 #include<cmath> 6 #include<vector> 7 #include<queue> 8 #define N 507 9 using namespace std; 10 11 int n; 12 int mp[N][N][4]; 13 int dis[N][N]; 14 15 struct dist 16 { 17 int x,y,dis; 18 bool operator < (const dist b) const 19 { 20 return dis>b.dis; 21 } 22 }; 23 priority_queue<dist>q; 24 int ans=1e9+7; 25 void insert(int x,int y,int d) 26 { 27 if(d<dis[x][y]) 28 { 29 dis[x][y]=d; 30 q.push((dist){x,y,d}); 31 } 32 if(y==1)ans=min(ans,d+mp[x][y][1]); 33 if(x==n)ans=min(ans,d+mp[x+1][y][0]); 34 } 35 void Dij() 36 { 37 int i,j; 38 for(i=1;i<=n;i++) 39 insert(1,i,mp[1][i][0]); 40 for(j=1;j<=n;j++) 41 insert(j,n,mp[j][n+1][1]); 42 while(!q.empty()) 43 { 44 dist now=q.top();q.pop(); 45 if(now.dis>dis[now.x][now.y])continue; 46 int x=now.x,y=now.y; 47 if(x>1) insert(x-1,y,now.dis+mp[now.x][now.y][2]); 48 if(y>1) insert(x,y-1,now.dis+mp[now.x][now.y][1]); 49 if(x<n) insert(x+1,y,now.dis+mp[now.x+1][now.y][0]); 50 if(y<n) insert(x,y+1,now.dis+mp[now.x][now.y+1][3]); 51 } 52 } 53 int main() 54 { 55 scanf("%d",&n); 56 for(int i=1;i<=n+1;i++) 57 for(int j=1;j<=n;j++) 58 scanf("%d",&mp[i][j][0]);//从西到东 59 for(int i=1;i<=n;i++) 60 for(int j=1;j<=n+1;j++) 61 scanf("%d",&mp[i][j][1]);//从北到南 62 for(int i=1;i<=n+1;i++) 63 for(int j=1;j<=n;j++) 64 scanf("%d",&mp[i][j][2]);//从东到西 65 for(int i=1;i<=n;i++) 66 for(int j=1;j<=n+1;j++) 67 scanf("%d",&mp[i][j][3]);//从南到北 68 memset(dis,0x3f,sizeof dis); 69 Dij(); 70 cout<<ans<<endl; 71 }




