软件工程作业No.3
软件工程第三次作业
一、作业选择
题目(1):最大连续子数组和(最大子段和)
背景:
问题: 给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
-- 引用自《百度百科》
二、作业程序
作业的程序链接
package fyz2;
public class Zixianghe {
public static int FindGreatestSumOfSubArray(int[] array) {
if (array.length==0 || array==null) {
return 0;
}
int currentSum = 0; //存储当前连续n项的和
int max = 0; //存储连续子元素和的最大值
for (int i = 0; i < array.length; i++) {
//核心部分,好好理解.
if(currentSum<=0){ //如过当前连续n项的和小于等于0,则没必要与后面的元素相加
currentSum = array[i]; //currentSum重新赋值
}else{
currentSum += array[i]; //如果currentSum的值大于0,则继续与后面的元素相加,
}
if(currentSum>max){ //每次改变currentSum的值都有与max进行比较
max = currentSum; //如果currentSum的值大于max,则将currentSum的值赋值给max
}
}
return max;
}
根据室友的推荐,我在CSDN的这篇文章上认真学习了最大连续子数组和的代码,由于我对Java语言的接触不是太多,所以理解起来有些吃力,不过作者的注释和相关解释十分到位,还是比较友好的~
三、测试部分
根据老师在作业要求中给的邹欣老师的这篇博文和《构建之法》的相关内容,以及CSDN大大的博文
中,我学习到了测试方法。
-
语句覆盖
使所有的判断语句都能执行一次的条件案例,例如当判断语句事组合语句的时候,并且用or连接,只满足一个案例即可 -
判定覆盖(分支覆盖)
针对判断语句,在设定案例的时候,要设定True和False的两种案例;与语句覆盖不同的是增加了False的情况

-
条件覆盖
针对判断语句里面案例的取值都要去一次,不考虑条件的取值

-
判定/条件覆盖
判定覆盖各条件覆盖交叉,针对于判定中的条件取值

-
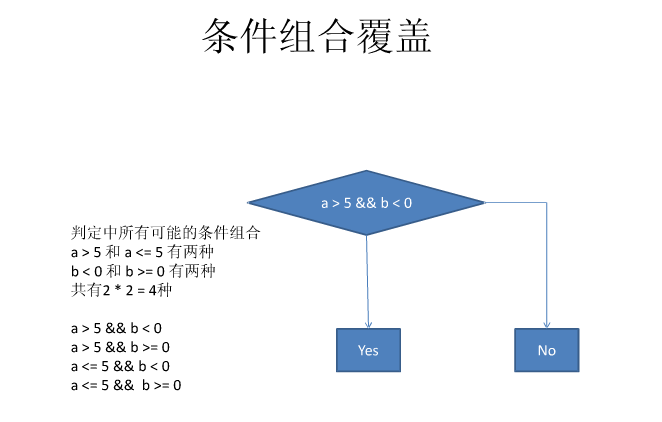
组合覆盖
判定-条件覆盖的加强版
附上我的测试代码:
public static void main(String[] args) {
int[] array = {};
int result = FindGreatestSumOfSubArray(array);
System.out.println(+result);
}
}
我选择条件组合覆盖
-
测试1,当所有的数值为负数时,输出结果正确
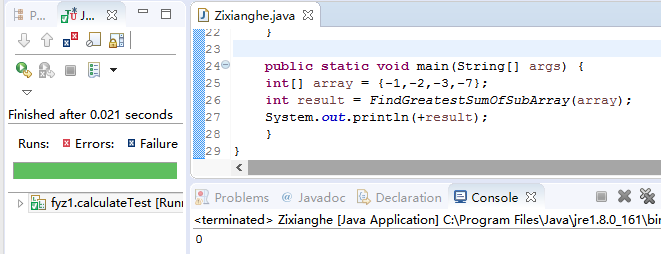
-
测试2,当所有数值为正数时,正确
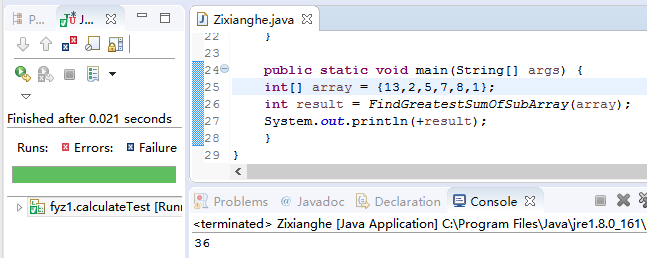
-
测试3,正确
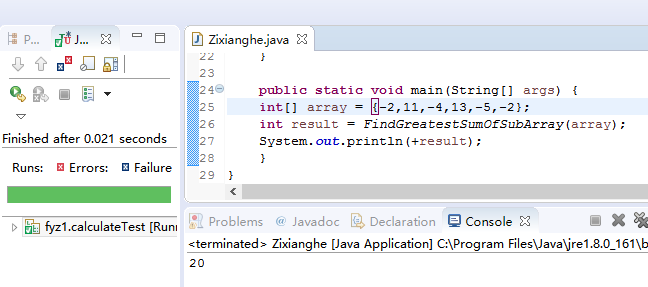
-
测试4,正确
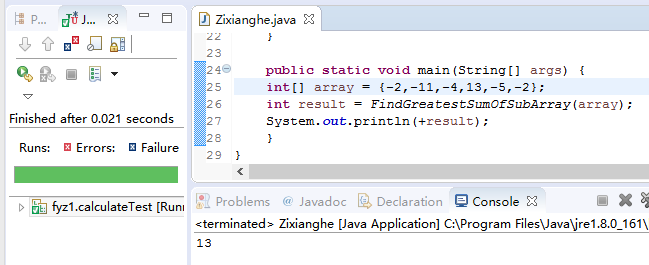
综上,该程序的测试通过。
四、心得
之所以选择Java的原因呢。。。。。。主要是因为我们五人组的大佬用这门语言,我也是半推半就开始摸索。说实话,面对一个陌生的事物,我有着一种本能的抵触,不愿去接触它,学习它。就我个人而言第二次作业就暴露出了很多的毛病(例如不愿编写代码,不愿做测试之类的)。在这次的作业中,感谢我室友对我的指导和帮助,外加老师在课堂上的悉心讲解,我学习了多种覆盖方法并有所理解,希望在接下来的课程中我还能学到更多有用的知识,不断提升自己。
[1]: https://blog.csdn.net/sd_lucky/article/details/52124183
[2]: http://www.cnblogs.com/xinz/archive/2011/10/22/2220872.html
[3]: https://blog.csdn.net/virus2014/article/details/51217026



