二叉树
树
什么是树?
这就是树:

我们现实生活中经常有这样的结构,比如企业层级关系:
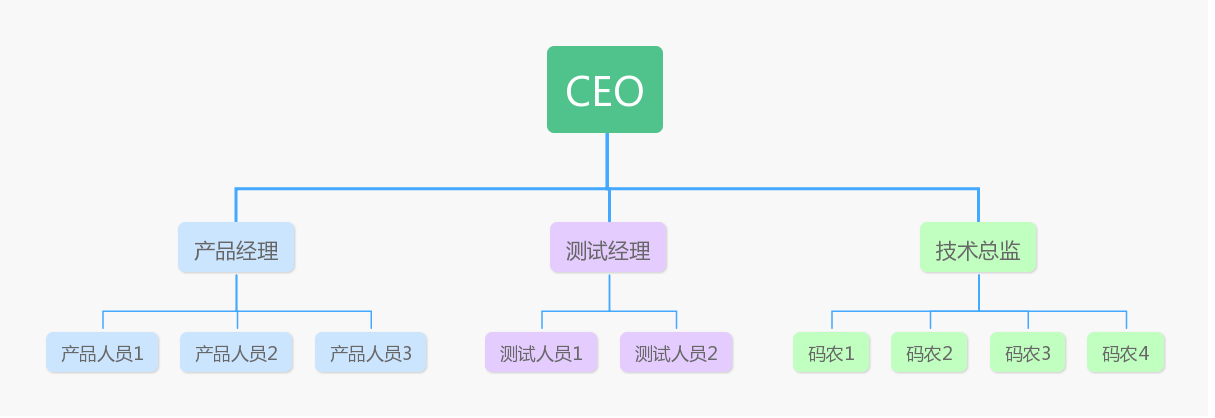
系统目录结构:
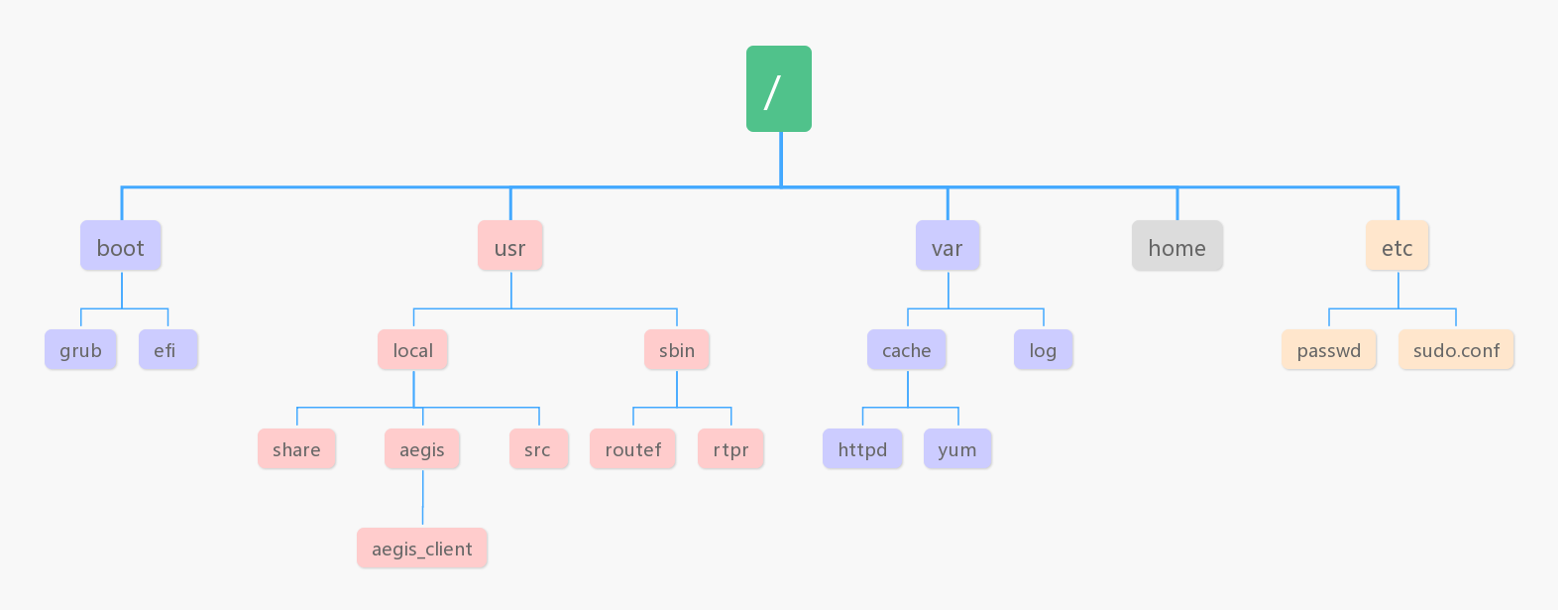
还比如家族族谱、书籍目录章节、后台系统页面上的菜单都是树形结构。
特别要注意的是,树是不包含回路的,如下图:
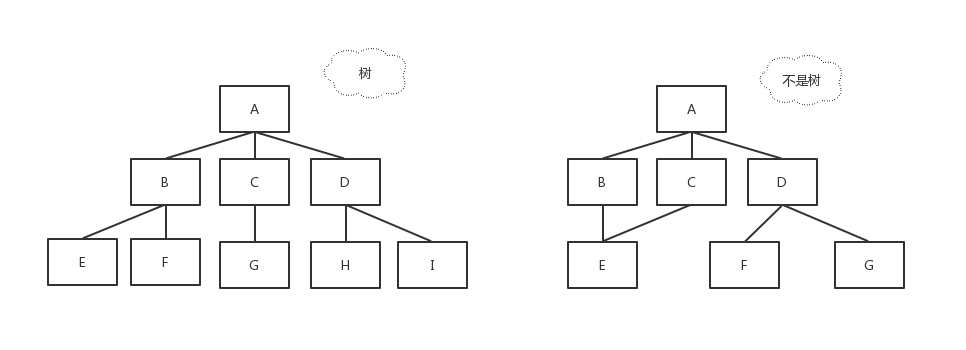
节点与树叶
一棵树中的所有组成部分叫做节点,由根节点伸展扩散,上下节点连接的关系称作父子关系。
如下面这棵树:
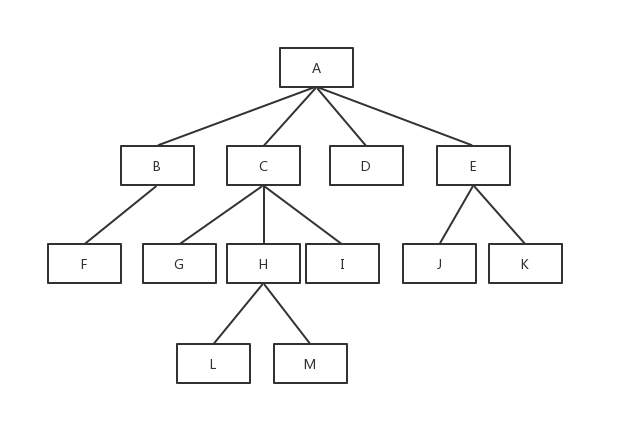
其中A节点就是根节点(root)。
B和F的关系就是父子关系,B是父(parent),F是子(child)。
B和C有共同的父节点,所以B和C的关系为兄弟节点(sibling)。
一棵树由N个节点组成,由于每个节点都有一条线连上父节点,唯独根节点没有父节点,所以一棵树总共有N-1条边。
每个节点可以有任意多个子节点,没有子节点的节点被称作这棵树的树叶(leaf)。
高度,深度与层数
还是这个示例:
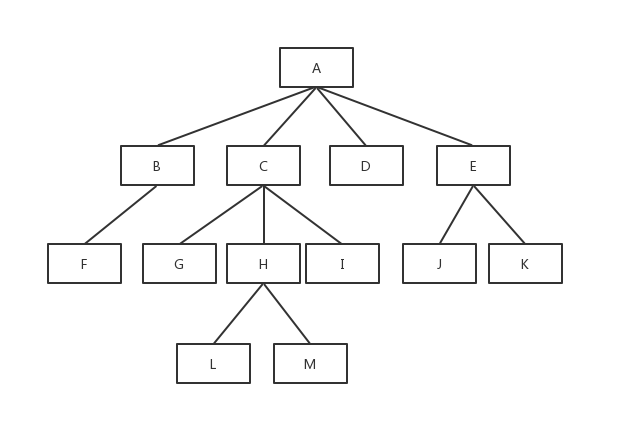
每个节点的高度是自身节点到当前分支的树叶的长度,比如B节点的高度为1,C节点的高度为2。
所有树叶的高度都是0,如F节点高度为0。
一棵树的高度等于它的根节点的高度。
每个节点的深度为根节点到自身的路径长度,比如C节点的深度为1,F的深度为2。
根节点的深度固定为0。
一棵树的深度等于它最深的那个树叶的深度。
层数和深度的计算差不多,不同之处是层数的计数起点是1,也就是说根节点位于整棵树的第1层。
二叉树基础
什么是二叉树?
顾名思义,二叉树的意思就是有两个叉的树,也就是每个节点最多只有两个子节点(最多的意思就是小于等于),分别叫做左子节点和右子节点。
如下图:
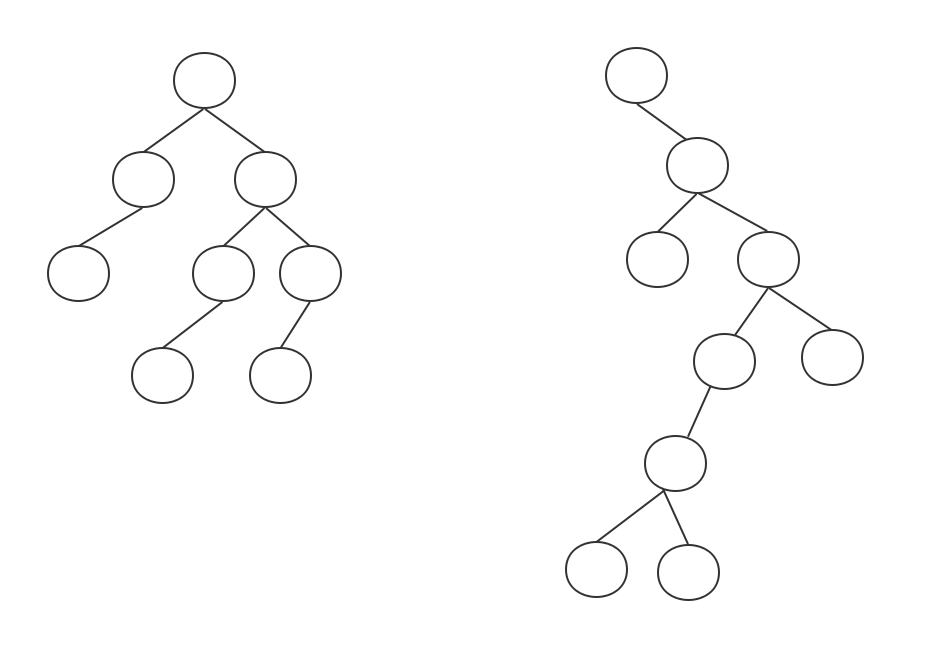
当然,也有四叉树、八叉树,之所以二叉树这么火,是因为二叉树的应用非常广泛。
二叉树还有两种特殊的表现形式,叫做满二叉树和完全二叉树。
满二叉树
如果一颗二叉树所有的叶子节点都有相同的深度,也就是整棵树除了叶子节点之外的所有节点都有两个子节点,那么这棵二叉树叫做满二叉树。
如下图:
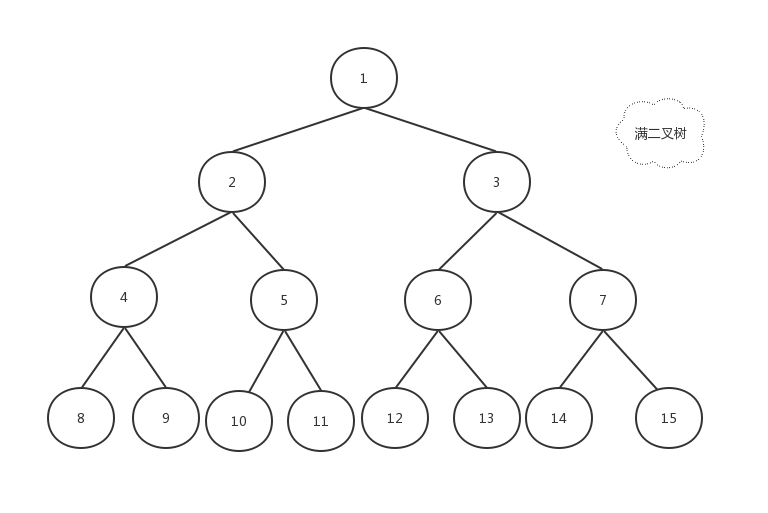
完全二叉树
如果一棵二叉树所有的叶子节点都在最底下两层,最后一层的叶子节点靠左排列,这种二叉树叫做完全二叉树。
也就是说,这棵二叉树快成满二叉树了,但是最后一层的叶子节点还没铺满,并且叶子节点是从左到右排列的叫做完全二叉树。
如图:
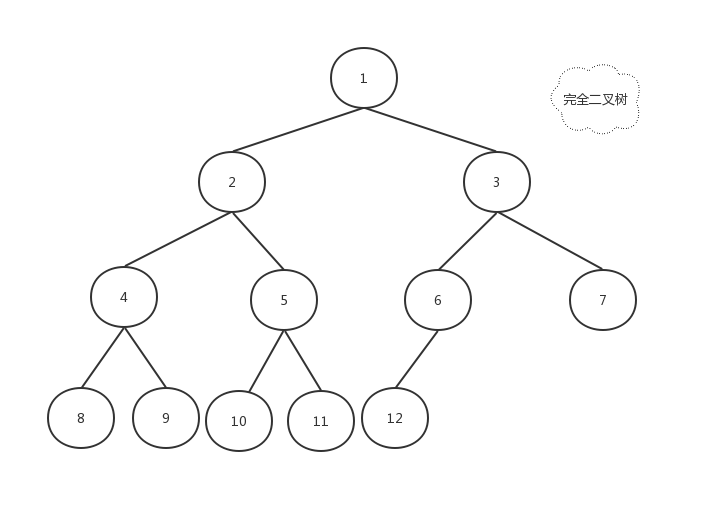
二叉树的存储
树这种结构并非物理存储结构,它需要使用数组或链表实现。
链式存储法
存储结构如图:
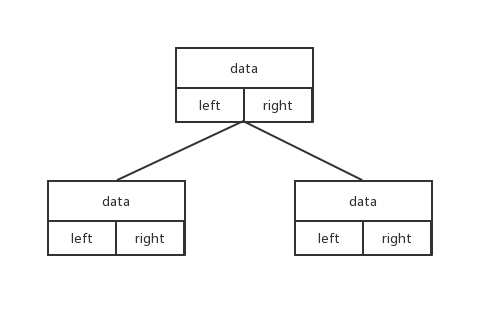
每个节点包含三部分:存储的数据、指向左子节点的指针,指向右子节点的指针。
节点属性:
class Node{ Object data; Node left; Node right; }
顺序存储法
用数组来存储,就应该将每个节点严格对应到数组下标上,鉴于二叉树最多只能两个叉,所以我们按照层级一层一层的排号。
如图:
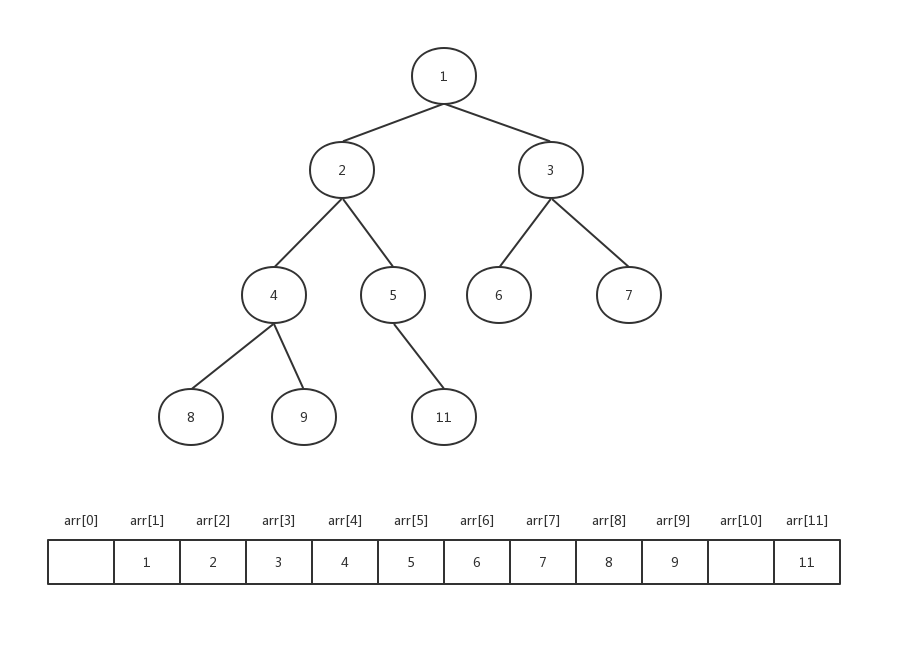
正常情况下,为了方便计算子节点,把整棵树串起来,我们将根节点存储在数组下标为1的位置,每一个节点的位置映射成数组下标。
假设每个节点的下标为i,那么我们可以得知每个节点的左子节点为 i*2,每个节点的右子节点为 i*2+1。
反之,每个节点的父节点的下标为 i / 2。
对于一棵满二叉树来说,用数组存储仅仅只空余了一个下标为0的数组空间。
那对于一棵稀疏的二叉树来说,用数组存储是比较浪费空间的,比如下面这棵非常牛逼的二叉树:
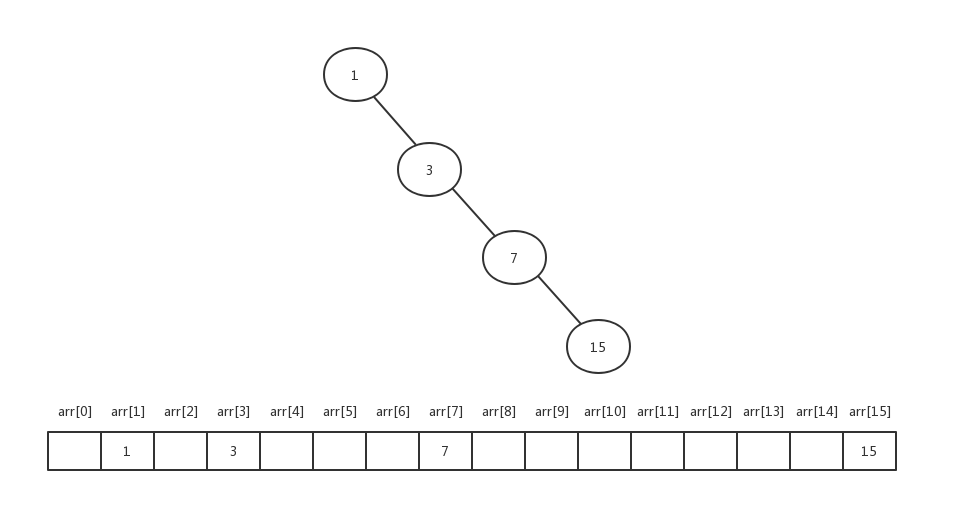
二叉查找树
什么是二叉查找树?
二叉查找树,也叫做二叉排序树,又叫二叉搜索树,这三个概念指的都是同一个东西,由名字可以得知,二叉查找树的特性是快速的增删改查。
二叉查找树在普通的树上添加了两个条件:
在树中的任意一个节点,其左子树中的每个节点的值,都要小于本身节点的值。
在树中的任意一个节点,其右子树上的每个节点的值,都要大于本身节点的值。
满足了这两个条件,那么这棵树就叫二叉查找树,整棵树中的每个节点的子树也就都是二叉查找树。
下图就是一棵二叉查找树:
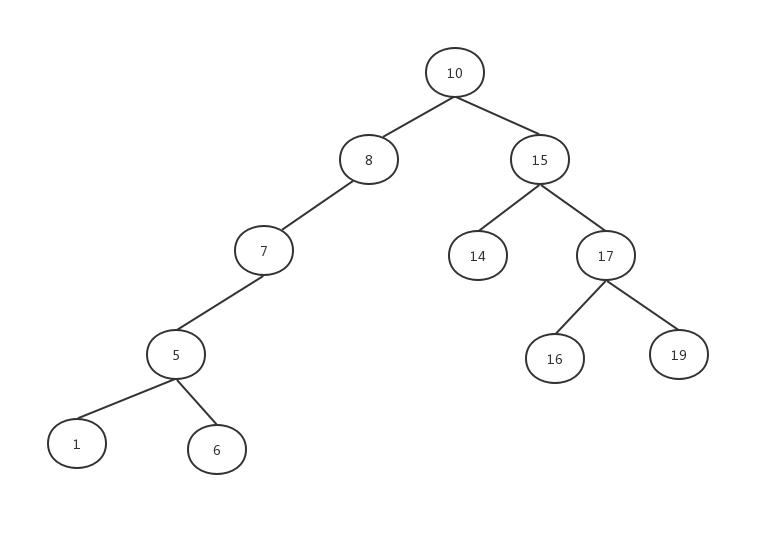
查找节点
假设我们要查找16这个数据,首先第一步找到根节点10:
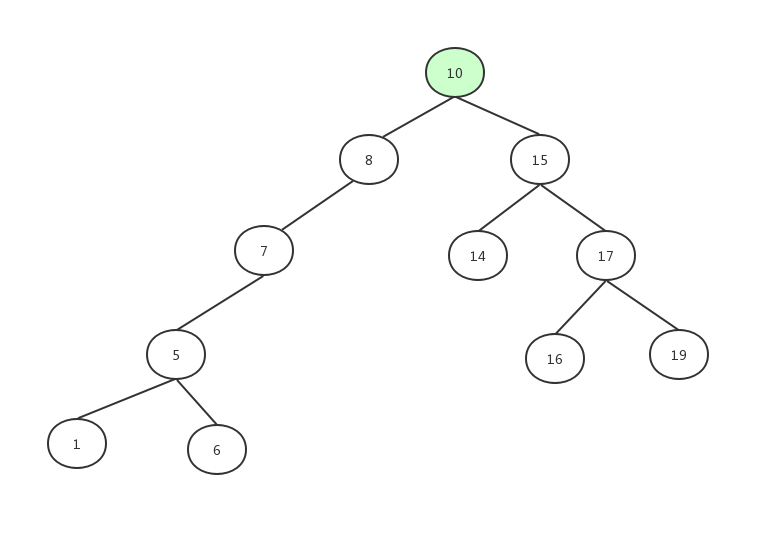
发现16大于10。
找到10的右子节点15:

发现16还是大于15。
继续找到15的右子节点17:
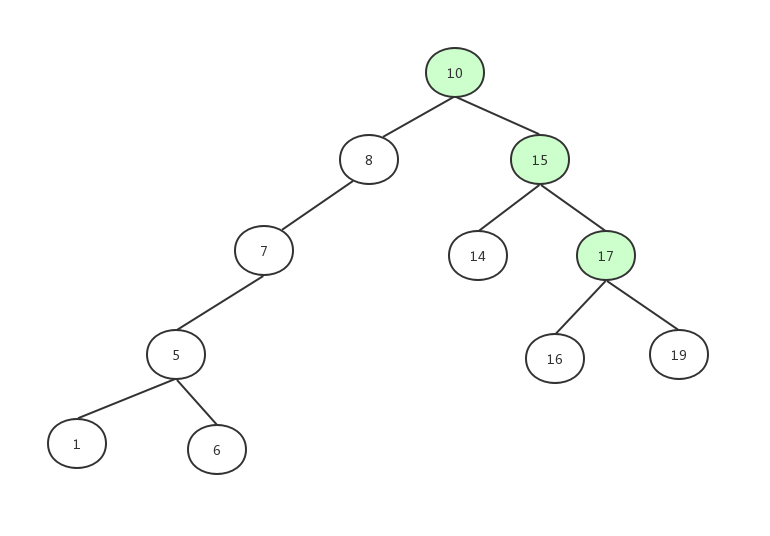
发现16小于17。
找到17的左子节点:
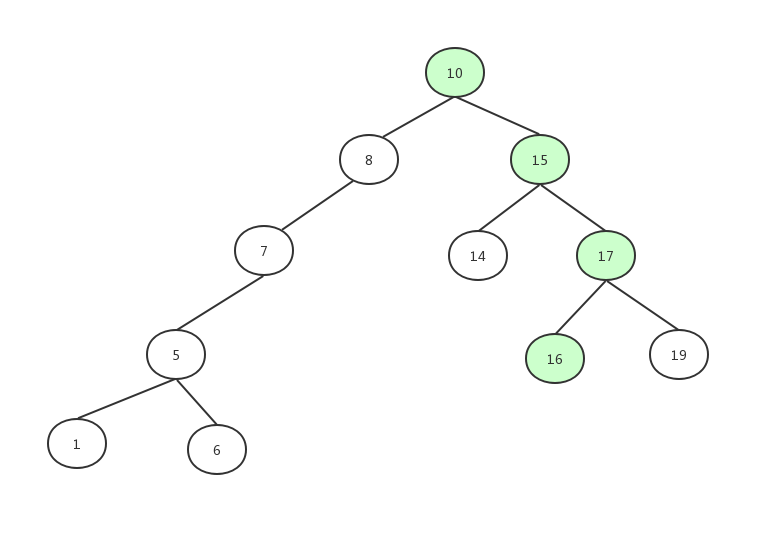
找到了16。
代码实现:
public Node find(int data) { while (null != node) { if(data == node.data){ return node; }else if(data < node.data){ node = node.left; }else if(data > node.data){ node = node.right; } } return null; }
最小节点和最大节点
由于小的节点总是在左子节点方向,因此我们可以用递归来实现找到整棵树中的最小节点:
public Node minNode(){ return minNode(tree); } private Node minNode(Node node) { if(null == node.left){ return node; } return minNode(node.left); }
最大节点也是一样,递归往右找,到底为止。
public Node maxNode(){ return maxNode(tree); } private Node maxNode(Node node) { if(null == node.right){ return node; } return maxNode(node.right); }
插入
新插入的节点,也要遵循二叉查找树的规则,逐一比较大小,比节点大就往右边,比节点小就往左边。
比如我们插入13这个元素,遵循规则的判断后最终位置会确定成14的左子节点。
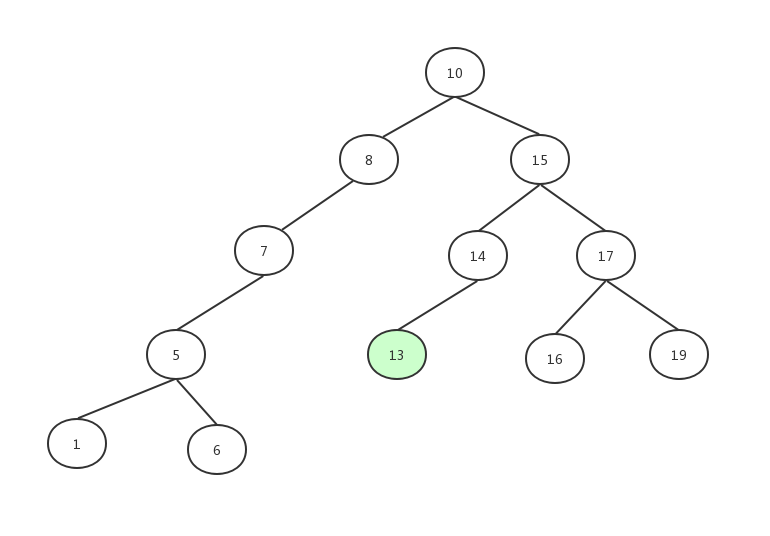
代码实现:
public void insert(int data) { Node newNode = new Node(data); if (null == tree) { tree = newNode;//如果整棵树不存在 那么新数据就是根节点 return; } while (null != tree) { if(data == tree.data){ return;//重复值 } //新元素大于当前节点 if (data > tree.data) { //右子节点有空位,则插入 if (null == tree.right) { tree.right = newNode; return; } tree = tree.right; } else { //新元素小于 if (null == node.left) { tree.left = newNode; return; } tree = tree.left; } } }
当我们依次插入10、8、15、7、14、17这几个元素后,二叉树的结构是这个样子的:

删除的三种情况
二叉查找树最难实现的就是删除,它要分三种情况
情况一:如果要删除的节点是叶子节点,比如我们要删除6这个节点
由于叶子节点没有子节点,所以只需要将它自身删除即可,也就是将该节点的父节点中指向它的指针置为null。
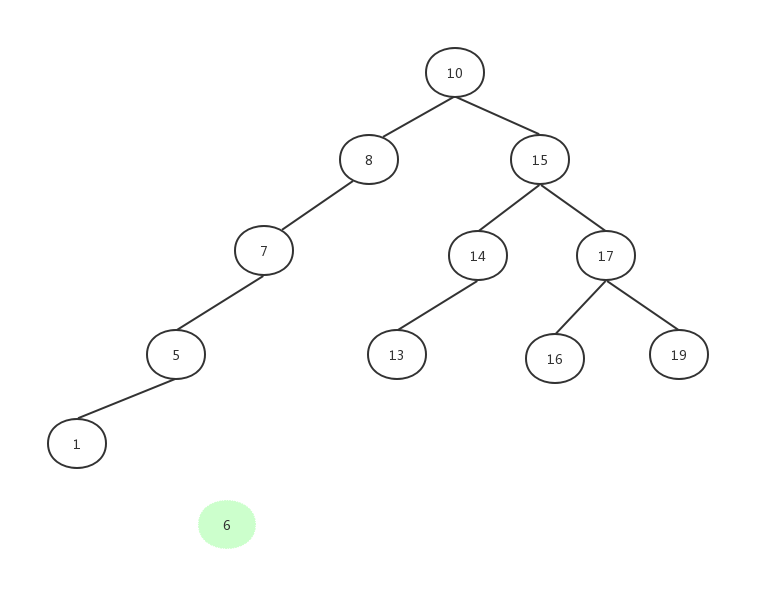
情况二:需要删除的节点含有一个子节点,比如我们要删除14这个节点
我们只需要把14拿掉,把14的子节点13连上14的父节点15就可以了

情况三:如果要删除的节点含有两个子节点,比如我们要删除15这个节点
这种情况也有两种做法。
其一是删除15这个元素,然后在15的右子树中查找最小的那个节点,替换到15的位置,结果如图:
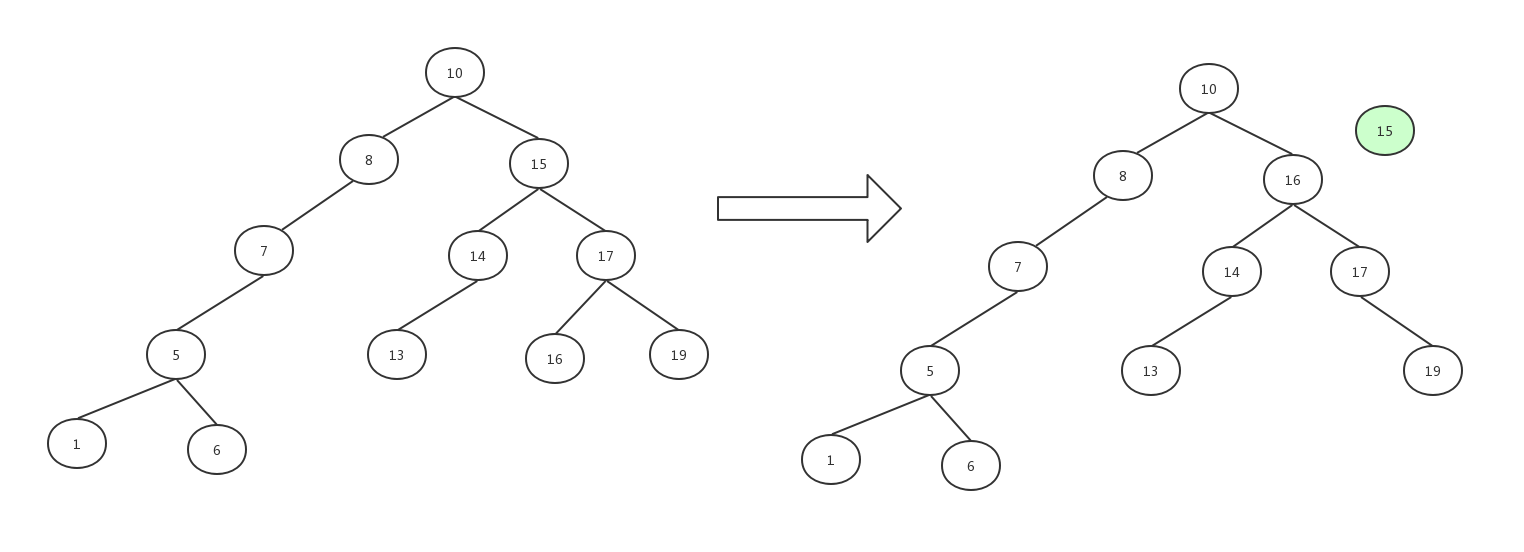
其二是删除15这个元素,然后在15的左子树中查找最大的那个节点,替换到15的位置,结果如图:
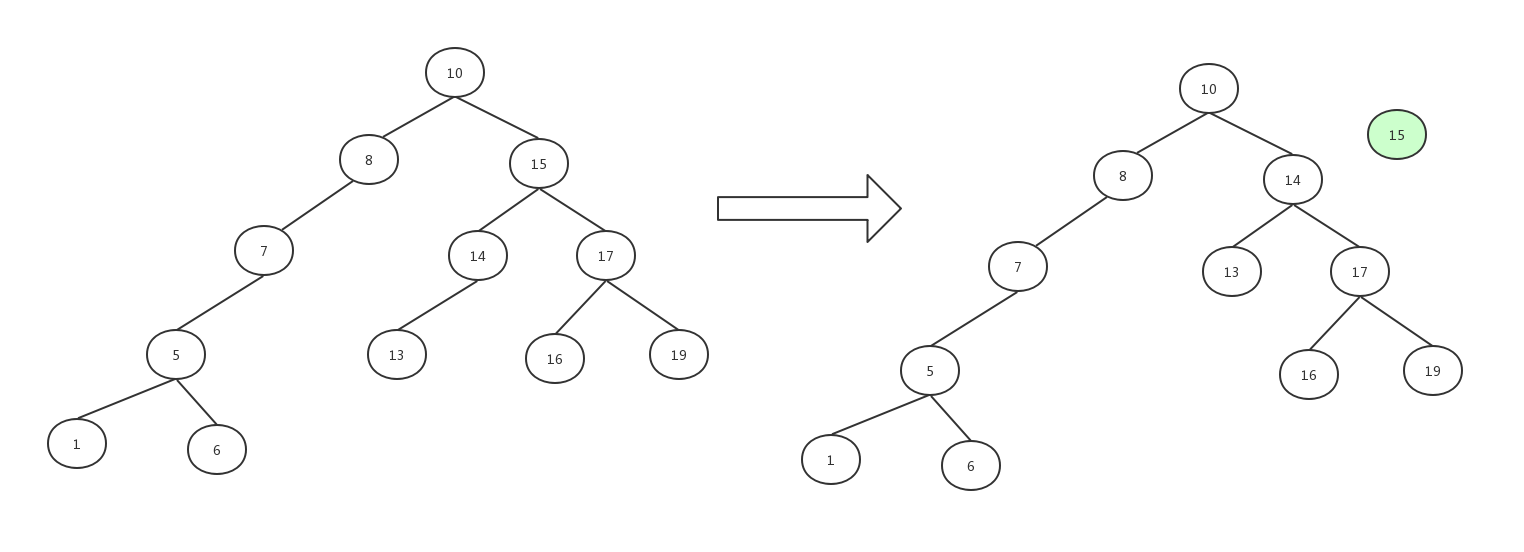
两种做法都可以满足二叉树的规则。
代码实现:
public void delete(int data) { Node deleteNode = tree; //目标删除节点 首先默认根节点 boolean is_find = false;//是否找到节点标记 Node deleteNodeParent = null; //目标删除节点的父节点 while (null != deleteNode) { if(deleteNode.data == data){ //找到了要删除的节点 is_find = true; break; } deleteNodeParent = deleteNode; if (data > deleteNode.data) { deleteNode = deleteNode.right;//如果要删除的数据比当前节点大,则往后边走。 } else { deleteNode = deleteNode.left;//如果要删除的数据比当前节点大,则往后边走。 } } //没有该节点 if (!is_find) { return; } // 要删除的节点有两个子节点 if (null != deleteNode.left && null != deleteNode.right) { // 查找右子树中最小节点 Node nodeMin = deleteNode.right;//右子树中最小节点 Node nodeMinParent = deleteNode; // 右子树中最小节点的父节点 while (null != nodeMin.left) { //只往左边找,最小的数据永远都在最左边 nodeMinParent = nodeMin; nodeMin = nodeMin.left; } deleteNode.data = nodeMin.data; // 将目标删除节点中的数据替换成右子树最小节点的数据,由于是引用传递,所以树(tree)中要删除的节点内容已经替换成了右子树中最小节点内容 deleteNode = nodeMin; //更新要删除的节点 转移删除目标 现在需要删除右子树中的最小节点 (程序走到这里 此时deleteNode是一定没有子节点的 因为它本身就是一个叶子节点) deleteNodeParent = nodeMinParent;//更新删除目标的父节点 } // 删除节点是叶子节点或者仅有一个子节点 Node childNode = null; // 接管被删除节点下面的子节点 //如果你有子节点 那么将子树拿出来 if(null != deleteNode.left){ childNode = deleteNode.left; }else if(null != deleteNode.right){ childNode = deleteNode.right; } //如果你要删的是根节点 if(null == deleteNodeParent){ tree = childNode; }else{ //处理被删除节点的父节点 将父节点的的指针指向下面的子节点 if(deleteNodeParent.left == deleteNode){ deleteNodeParent.left = childNode;//如果是在父节点的左子节点 则把子节点对接给父节点的left }else{ deleteNodeParent.right = childNode;//如果是在父节点的右子节点 则把子节点对接给父节点的right } } }
虽然我们没有真实的去做删除节点这个操作,但是更改了引用之后,它很快就会被垃圾收集器清理掉。
懒惰删除
由于删除工作要沿着整棵树进行两趟搜索,所以它的效率是有提升空间的,因此在二叉查找树的删除方面还有一个方案,叫做懒惰删除。
懒惰删除的做法是删除一个元素时候,只是将它标记为已删除,并不是真正的把这个节点删掉,它仍然存留在树中,只是属性里多了一个标记。
懒惰删除使删除操作变的简单,但缺点是比较浪费空间,只有确定删除的次数很少的时候几乎才会考虑,并且遍历时却需要对整棵树重新排序,因此个人认为这种删除方式更加麻烦,绝大部分实现二叉树的开发者都不会采用懒惰删除这种方法。
二叉树的遍历
深度优先遍历
深度优先遍历的思想很简单,就是一条线先走到尽头,再回头走另一条线。
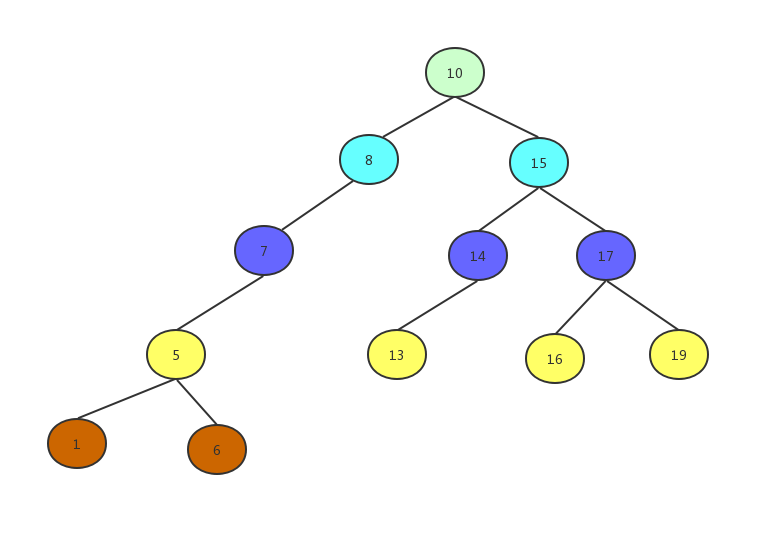
以如下这棵树为例,首先遍历出 10->8->7->5->1
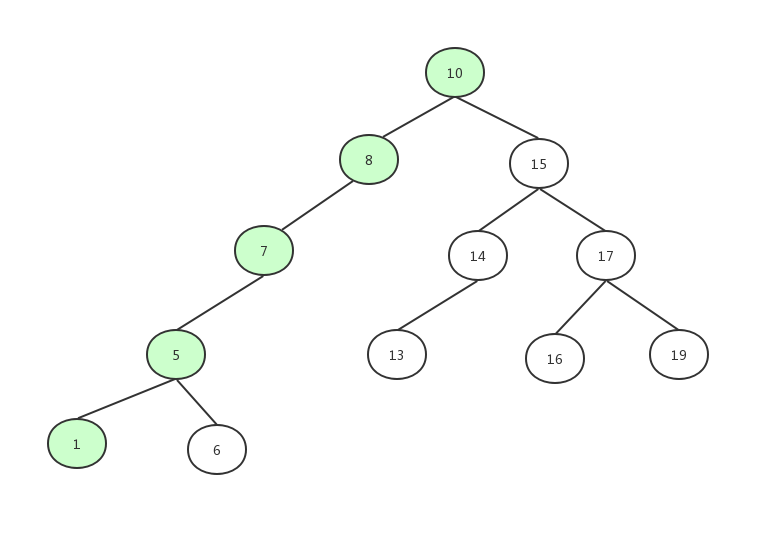
然后再遍历出 6
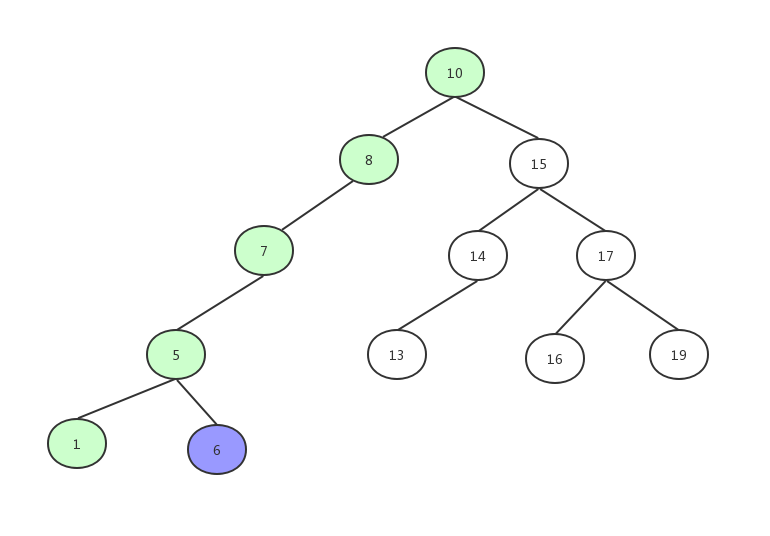
然后是 15->14->13
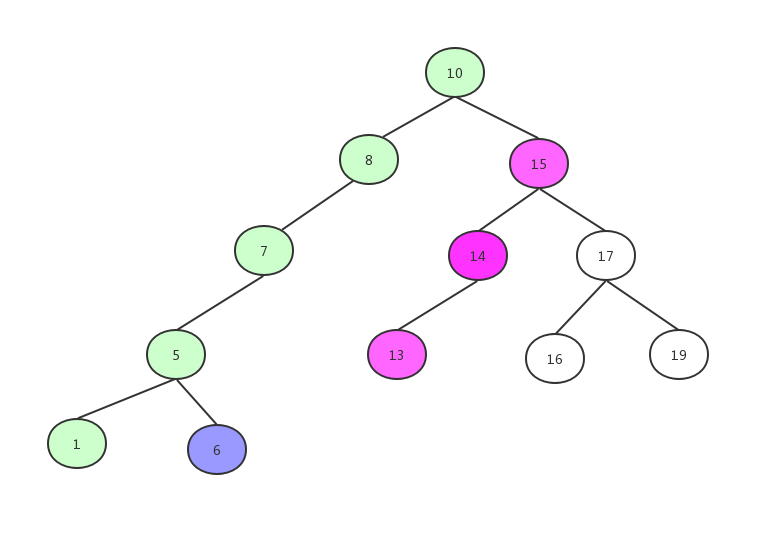
然后是17->16
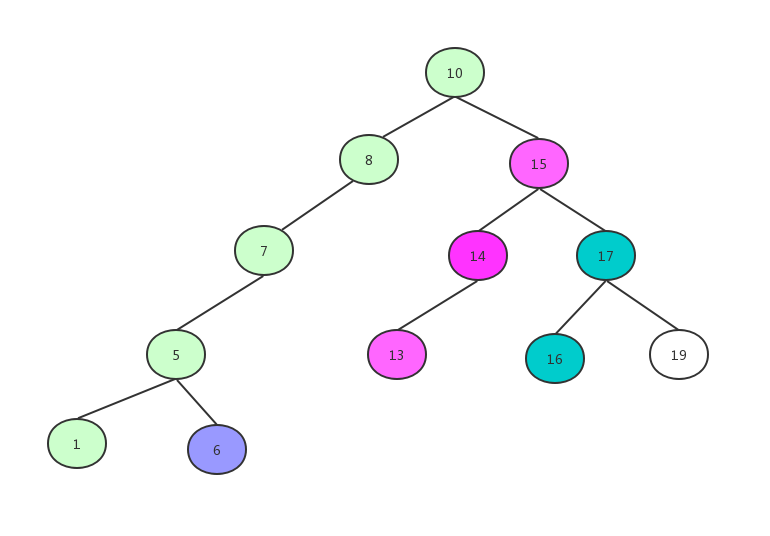
最后是19
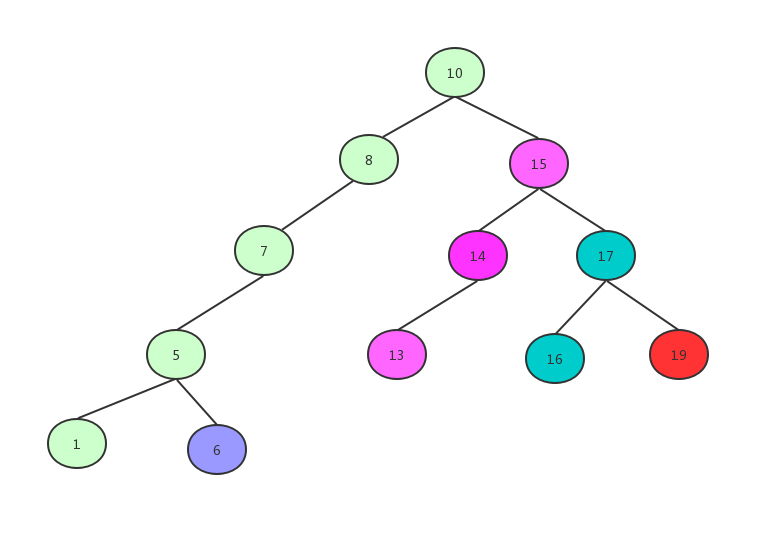
代码:
public void preTraversal(Node node){ if(node == null){ return; } System.out.println(node.data); preTraversal(node.left); preTraversal(node.right); }
广度优先遍历
广度优先遍历还有另一种称呼叫层序遍历,像洋葱一样一层一层的剥,如下图:
这种遍历需要借助队列来完成:
public static void levelTraversal(Node root){ if(null == root){ return; } Queue<Node> queue = new LinkedList<>(); queue.offer(root);//初始化 while(!queue.isEmpty()){ Node node = queue.poll();//弹出节点 System.out.println(node.data);//打印 if(node.left != null){ queue.offer(node.left);//左子节点入队 } if(node.right != null){ queue.offer(node.right);//右子节点入队 } } }
最后:感谢阅读。


