算法原理与实践（动态规划与递归）
大纲
- 动态规划和递归介绍
- 基本思路
- 记忆化搜索
- 经典例题
- 总结（矩阵，序列动态规划 ）
1. 动态规划和递归介绍
递归和动态规划比较
相同：都能分解成若干子问题。
不同：DP 存储子问题结果。
动态规划介绍
- 算法的核心在于找到状态转移方程
- Build approach from sub-problems to the final destination
- Recursion的空间与时间成本
- Bottom-Up与Top-Down
- 主问题分解成子问题，自底向上/自顶向下。
- 通往问题的 solution 如果有子问题的重复计算，则可以存储中间结果，用空间换时间。
DP 与贪心的区别
- DP 记录通往全局最优解的局部解，计算后面的子问题时可以考虑前面问题的解。
- 贪心只记录当前最优解，前面问题的解会被覆盖掉。
- DP：数组存中间结果；贪心：仅一个变量存中间结果。
自底向上 DP 与 memorization DP
自底向上 DP
- 难于理解
- 边界条件难于处理
- 只适合问题的结点空间是离散的整数空间。每一步的计算必须是连续的整数计算
memorization DP
- 适用于由递归改 DP
- 子问题仅在被需要时才计算
Fibonacci Number
1, 1, 2, 3, 5…
NON-Dynamic Programming
自顶向下
int Fibonacci(int n) {
if(n == 0)
return 0;
if(n == 1)
return 1;
return Fibonacci(n-1) + Fibonacci(n-2);
}
For fib(8), how many calls to function fib(n)?
DP
avoid repeated calls by remembering function values already calculated
自底向上
int Fibonacci(int n) {
int array[n] = {0};
array[1] = 1;
for (int i = 2; i < n; i++)
array[i] = array[i-1] + array[i-2];
return array[n];
}
动态规划的4点要素
- 状态 (存储小规模问题的结果）
- 方程 (状态之间的联系，怎么通过小的状态，来算大的状态)
- 初始化 (最极限的小状态是什么)
- 答案 (最大的那个状态是什么)
Memorization
Memorize Search 记忆化搜索
Advantage: Easy to think and implement.
Disadvantage: Expensive memory cost.
T func(N node, HashTable<N, T>& cache) {
if (cache.contains(node)) {
return cache.get(node);
}
…
T sub_res = func(next_node, cache);
…
//当前子问题的解，依赖于更小的子问题(s)
T res = G( sub_res … );
cache.set(node, res);
return res;
}
算法策略比较
- Divide and Conquer：merge sort、quick sort、每个部分都不能重叠，合并部分结果
- Dynamic Programming：尽量地不重复计算每个子问题，把计算结果存储下来，作为后续问题的解
- Greedy Algorithm：只做出当前最优的判断，不考虑对全局的影响，每次更新只是当前最优解
- Backtracking：穷举、暴力深搜
模式识别
- 用Dynamic Programming (Bottom-Up) 解决收敛结构问题
收敛问题
聚合相关的属性，比如：特殊的解、最优的值、总和、数量的问题。然后把整数坐标映射成节点（这一步也可以称为“离散”），当前节点值只依赖于前驱结点。
例如对于斐波那契数列，有递推式：
f(n) = G[f(n-1), f(n-2)] = f(n-1) + f(n-2)
可以把上述递推关系写在手边，这样做非常有利于理清算法实现的思路。
如果出现类似于“所有解”，“所有路径”等关键词，则用 Top-down 方法更为
直接。
Climbing Stairs
Suppose we have a ladder which has n steps. Each time you can either climb 1 or 2 steps. Please write a function to calculate how many distinct ways that can you climb to the top?
CountOfWays(n) = CountOfWays(n–1) + CountOfWays(n-2);
Prime
Compute the nth prime
2, 3, 5, 7…
第 n 个素数 => 特殊解问题 => DP => 动归方程很重要
事实上，素数的定义中就隐含了递归关系：如果 n 是素数，那么 n 不能被 1 ~ n-1 的所有素数整除。
Prime(n) = G ( Prime(n-1), Prime(n-2), Prime(n-3) … Prime(1));
Prime(1) = 2
G( )表示不能整除的关系。
#define PRIME_TYPE unsigned long int
PRIME_TYPE getNthPrime(const unsigned int n) {
vector<PRIME_TYPE> v = { 2, 3};
PRIME_TYPE last = v[v.size() - 1] + 2;
while (v.size() < n) {
vector<PRIME_TYPE>::iterator it = v.begin();
bool isPrime = false;
while (it != v.cend()){
if (last % *it++) {
isPrime = true;
}
else {
isPrime = false;
break;
}
}
if (isPrime)
v.push_back(last);
last += 2;
}
return v[n - 1];
}
Word Break
Given an input string and a dictionary of words, check if the input string can segment into a space-separated sequence of dictionary words if possible.
For example, if the input string is "applepie" and dictionary contains a standard set of English words, then we would return true since the string "apple pie” is found in dict.
Palindrome Partition
Given a string s, we can partition s such that every segment is a palindrome (e.g, ‘abba’ is a palindrome, ‘a’ is a palindrome, ‘ab’ is not).
Please write a function to return the minimum cuts needed for a palindrome partitioning, given string s.
本题可以分为两个部分：
- 判断字串是不是回文(palindrome)
- 切割原字符串。
递推公式：
isPalindrome( i , j ) = (value(i) == value(j)) AND ( isPalindrome(i+1, j-1) OR j – i <= 1 )
i和j分别表示 substring 的首坐标和尾坐标
minCut(i) = min(minCut(j+1)+1)，for i <= j < n, and substring(i , j) is palindrome。
解题代码
int minCut(string s) {
vector<vector<bool> > palin(s.size(),vector<bool>(s.size(), false));
vector<int> table(s.size() + 1, 0);
for (int i = 0; i <= s.size(); i++)
table[i] = s.size() - i - 1;
for (int i = s.size() - 1; i >= 0; i--) {
for (int j = i; j < s.size(); ++j) {
if (s[i] == s[j] && (j - i <= 1 || palin[i + 1][j - 1])) {
palin[i][j] = true;
table[i] = min(table[j + 1] + 1, table[i]);
}
}
}
return table[0];
}
（题目取自 leetcode 132. Palindrome Partitioning II）
** “聚合”性质**
求最值或者求和问题，往往可以进一步优化DP Table的空间。
如果只在乎紧邻的前一个的局部解，而不在乎前几个局部解的问题，就
可以接受每次在计算当前解的时候，替换掉那个最优解。
Unique Path（leetcode 62）
How many paths are there for a robot to go from (0,0) to (x,y),
supposing it can only move down and move right.
递推公式如下：
countOfWays[i][j]=countOfWays[i-1][j]+countOfWays[i][j-1]
其中，i 和 j 分别表示起点的横纵坐标。
解法一 未作 DP table 空间优化
class Solution {
public:
int uniquePaths(const int m, const int n) const {
vector<vector<int>> vv(m, vector<int>(n, 1)); //DP table
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
vv[i][j] = vv[i][j - 1] + vv[i - 1][j];
}
}
return vv[m - 1][n - 1];
}
};
解法二 DP table 优化后
class Solution {
public:
int uniquePaths(const int m, const int n) const {
if (m == 1 || n == 1) return 1;
int max = m > n ? m : n;
int min = m > n ? n : m;
vector<int> v(max);
for (vector<int>::size_type i = 0; i < v.size(); i++)
v[i] = i + 1;
for (int j = 2; j < min; j++) {
for (int i = 1; i < max && max > 2; i++)
v[i] += v[i - 1];
}
return v[v.size() - 1];
}
};
Unique Path II (leetcode 63)
Now consider if some obstacles are added to the grids. How many unique paths would there be?
An obstacle and empty space is marked as 1 and 0 respectively in the grid. There is one obstacle in the middle of a 3x3 grid as illustrated below.
[
[0,0,0],
[0,1,0],
[0,0,0]
]
The total number of unique paths is 2.
递推公式
- 当(i, j)有障碍时dp[i][j] = 0
- dp[0][j]和dp[i][0]未必为1.
dp[0][j] = obstacleGrid[0][j] ? 0 : dp[0][j-1]
dp[i][0] = obstacleGrid[i][0] ? 0 : dp[i-1][0]
- 当obstacleGrid [0][0] = 1时，return 0
Minimum Path Sum
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its
path.
Note: You can only move either down or right at any point in time.
解题思路
递推公式如下
dp[i][j] = min(dp[i][j-1], dp[i - 1][j]) + grid[i][j]
Jump Game
Given an array of non-negative integers, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Determine if you are able to reach the last index.
For example:
A = [2,3,1,1,4], return true.
A = [3,2,1,0,4], return false.
Triangle
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.（只能向下、右下,两个方向）
For example, given the following triangle
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
96. nique Binary Search Trees
Given n, how many structurally unique BST's (binary search trees) that
store values 1...n?
For example, Given n = 3, there are a total of 5 unique BST's.
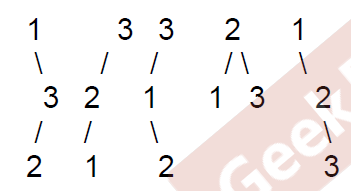
解题思路
dp[i] = sum(dp[k] * dp[i - k -1]) 0 <= k < i
伪代码描述
for(i = 0; i <=n; i++)
for(k = 0; k < i; k++)
dp[i] += dp[k] + dp[i - k - 1]
然后再考虑边缘case，因为 dp[i-k-1] 的存在，所以 i >= k + 1，又因为 0<= k < i，所以 i >= 1。
本题的解法属于“自底向上” DP，所以需要在 dp table 的开始位置“预设”一些基础值，以供后面使用。所以需要在开始时设置 dp[0] = 0, dp[1] = 1。
代码实现
class Solution {
public:
int numTrees(int n) {
vector<int> dp(n + 1, 0);
//dp初始化
dp[0] = 1;
dp[1] = 1;
for(int i = 2; i <= n; i++) {
for(int k = 0; k < i; j++) {
//如果左子树的个数为j，那么右子树为i - k - 1
dp[i] += dp[k] * dp[i - k - 1];
}
}
return dp[n];
}
};
Coin Change(not found in Leetcode)
Given a value N, this N means we need to make change for N cents, and we have infinite supply of each of S = { S1, S2, .. , Sm} valued coins, how many ways can we make the change?
递推公式
ways(i, j) = ways(i-s(j), j) + ways(i, j-1); i ∈ [0,N], j ∈ [1,m]
代码实现
int countWays(vector<int> S, int m, int n) {
vector<int> table(n+1, 0);
table[0] = 1;
for(int i = 1; i <= n; i++)
for(int j = 0; j < m; j++)
table[i] += (i-s[j] >= 0) ? table[i-S[j]] : 0;
return table[n];
}
Coin Change 2(no identical in Leetcode)
Given a value N, this N means we need to make change for N cents, and we have infinite supply of each of S = { S1, S2, .. , Sm} valued coins. Please implement a function which gets the minimal number of coins for N cents.
递推公式
minNum(i, j) = min( minNum(i-s(j), j) + 1, minNum(i, j-1) ); i ∈ [0,N], j ∈ [1,m]
代码实现
int minNum(vector<int> S, int m, int n) {
vector<int> table(n+1, INT::MAX);
table[0] = 0;
for(int i = 1; i <= n; i++)
for(int j = 0; j < m; j++) {
if( i >= s[j] && table[i] > table[i-s[j]])
table[i] = table[i-s[j]] + 1;
}
return table[n];
}
最长子序列的问题
对于“最长子序列”问题(即有限空间内，满足一定条件的最长顺序子序列)，本身具有很强的聚合性，可以以如下方式解答：用DP Table来记录以当前节点为末节点的序列的解(至少固定问题的一端，因此不是以“当前节点或之前节点”为末节点的解)，并根据递推关系，由问题空间的起点到达问题空间的终点。
Longest Sub Sequence(Leetcode 300)
Find the longest increasing subsequence in an integer array. E.g, for array {1, 3, 2, 4}, return 3.
递推公式
maxLength(i) = max{ maxLength(k), k = 0~i-1 and array[i] > array[k] } + 1;
心得体会：
- 由 0 <= k <= i - 1 可以得知，在两层嵌套的循环中，永远不会和自己比较。
- 本节点的值，只与第k个节点有关。
代码实现
class Solution {
public:
int lengthOfLIS(vector<int> &arr) {
if (arr.size() < 1) return 0;
//如果位置0总是少1，那么初始化时就都赋成1
vector<int> table(arr.size(), 1);
for (size_t i = 0; i < arr.size(); i++)
//DP的特点：k永远从0起、永远不等于i
for (size_t k = 0; k < i; k++)
if (arr[i] > arr[k] && table[k] + 1 > table[i])
table[i] = table[k] + 1;
return *max_element(table.begin(), table.end());
}
};
Gas Station
Suppose you are traveling along a circular route. On that route, we have N gas stations for you, where the amount of gas at station i is gas[i]. Suppose the size of the gas tank on your car is unlimited. To travel from station i to its next neighbor will cost you cost[i] of gas. Initially, your car has an empty tank, but you can begin your travel at any of the gas stations. Please return the smallest starting gas station's index if you can travel around the circuit once, otherwise return -1.
解题思路
对于第 i 个加油站，它能给车子提供的净动力为 array[i] = gas[i] – cost[i]
问题转化为，找到一个起始位置 index，将 array 依此向左 shift（位移），即 index -> 0 (index对应新的数组下标 0 )， index + 1 -> 1…，使得对于任意 0 <= i < n，满足序列和 subSum( 0, i) 大于 0。
首先考虑什么情况下有解，接下来考虑如何选择一个正确的起始点。
（详细解答见 《程序员面试白皮书》 P185）
代码实现
int canCompleteCircuit(vector<int> &gas, vector<int> &cost) {
int size = gas.size();
int subSum = 0, sum = 0;
int array[gas.size()];
int index = 0;
for(int i = 0; i < size; i++){
array[i] = gas[i] - cost[i];
sum += array[i];
}
if (sum < 0)
return -1;
for(int i = 0; i < size; i++) {
subSum += array[i];
if(subSum < 0) {
subSum = 0;
index = i + 1;
}
}
return index;
}
Longest Common Sequence
Please write a function to calculate the Longest Common Subsequence (LCS) given two strings.
LCS for input Sequences “ABCDGH” and “AEDFHR” is “ADH” of length 3.
LCS for input Sequences “AGGTAB” and “GXTXAYB” is “GTAB” of length 4.
解题思路
递推公式如下
Length(i,j) = (str1[i-1] == str2[j-1]) ? Length(i-1, j-1) + 1 ： Max { Length(i,j-1), Length(i-1,j) }
LCS 问题是很经典的研究对象，可以考虑成在二维数组上的运算，如图所示。
其递推公式可以描述成
LCS(x,y,i,j)
if x[i] = y[j]
then
C[i,j] ← LCS(x,y,i-1,j-1)+1
else
C[i,j] ← max{LCS(x,y,i-1,j),LCS(x,y,i,j-1)}
return C[i,j]
代码实现
unsigned int lcs(const string &lhs, const string &rhs) {
unsigned int row = lhs.length() + 1;
unsigned int col = rhs.length() + 1;
vector<vector<unsigned int>> table(row, vector<unsigned int>(col));
for (unsigned int r = 1; r < row; r++) {
for (unsigned int c = 1; c < col; c++) {
if (lhs[r] == rhs[c]) {
table[r][c] = table[r - 1][c - 1] + 1;
}
else {
table[r][c] = max(table[r - 1][c], table[r][c - 1]);
}
}
}
return table[row - 1][col - 1];
}
模式识别
如果当前节点的解，既依赖于前驱问题的解，又依赖于后驱问题的解，但这两部分又互相独立，则可以分别自左开始 DP，计算从最左节点到当前节点的结果；然后自右开始 DP，计算从最右节点到当前节点的结果；再用同一个DP Table来合并解。
238. Product of Array Except Self My Submissions QuestionEditorial Solution
Given an array of n integers where n > 1, nums, return an array output such that output[i] is equal to the product of all the elements of nums except nums[i].
Solve it without division and in O(n).
For example, given [1,2,3,4], return [24,12,8,6].
Follow up:
Could you solve it with constant space complexity? (Note: The output array does not count as extra space for the purpose of space complexity analysis.)
解题思路
首先可以把输入序列考虑成矩阵展开形式
1 2 3 4
1 x
2 x
3 x
4 x
那么，递推公式可以展开成如下形式：
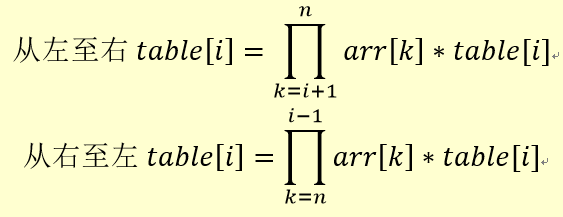
用伪代码表示当序列有四项时，DP的运算过程：
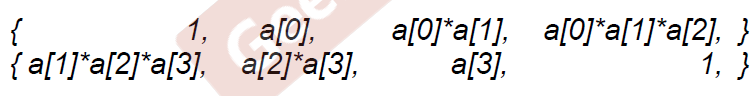
代码实现1
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
vector<int> table(nums.size(), 1);
for (size_t i = 0; i < nums.size(); i++) {
for (size_t k = 0; k < i; k++) {
table[i] *= nums[k];
}
}
for (size_t i = nums.size(); i > 0; i--) {
for (size_t k = nums.size(); k > i; k--) {
table[i-1] *= nums[k-1];
}
}
return table;
}
};
但是这样的解法时间复杂度为
O(n^2)
但是提交时发现超时了。
Hold Water
You are given an array of n non-negative integers. Each value means the height of a histogram. Suppose you are pouring water onto them, what is the maximum water it can hold between a left bar and a right bar (no separation)?
解题思路
当前节点的储水量，等于左侧最高海拔与右侧最高海拔的较小值减去当前节点的海拔。
代码实现
int trap(int A[], int n) {
if(n <= 0) return 0;
vector<int> dp(n,0);
int left_max = 0, right_max = 0,water = 0;
for(int i = 0; i < n; i++) {
dp[i] = left_max;
if(A[i] > left_max)
left_max = A[i];
}
for(int i = n -1; i >= 0; i--) {
if(min(right_max, dp[i]) > A[i])
water += min(right_max,dp[i]) - A[i];
if(A[i] > right_max)
right_max = A[i];
}
return water;
}
模式识别
- 用 Memorization Technique(Top-Down) 解决收敛结构问题。
Memorization 是 Top-Down 形式的 Dynamic Programming，也可以用来解决前述的问题(但空间上可能效率不及 Bottom-Up 形式的 DP)。
Memoization 的核心在于，在原有递归框架下，储存子问题的计算结果，在重复计算子问题时可以直接返回已经计算的值。
Tallest stack of boxes
Given a set of boxes, each one has a square bottom and height of 1. Please write a function to return the tallest stack of these boxes. The constraint is that a box can be put on top only when its square bottom is restrictively smaller.
vector<Box> createStackDP( Box boxes[], const int num, Box bottom, unordered_map< Box, vector<Box> >& stackCache) {
vector<Box> max_stack;
int max_height = 0;
vector<Box> new_stack;
// memorization
if( stackCache.count( bottom ) > 0 )
return stackCache[ bottom ];
else {
for( int i = 0; i < num; i++ ) {
if( Box[i].canBeAbove( bottom ) ) {
// solve subproblem
new_stack = createStackDP( boxes, num, Box[i], stackCache );
}
if( new_stack.size() > max_height ) {
max_height = new_stack.size();
max_stack = new_stack;
}
}
}
max_stack.insert( max_stack.begin(), bottom );
stackCache[ bottom ] = max_stack;
return max_stack;
}
Word Break II
Given a string and a dictionary of words, please write a function to add space into the string, such that the string can be completely segmented into several words, where every word appears in the given dictionary.
代码实现
vector<string> wordBreak(string s, unordered_set<string> &dict, unordered_map<string,vector<string> >& cache) {
// memorization
if(cache.count(s))
return cache[s];
vector<string> vs;
if(s.empty()) {
vs.push_back(string());
return vs;
}
for(int len = 1; len <= s.size(); ++len ) {
string prefix = s.substr(0,len);
if(dict.count(prefix) > 0) {
string suffix = s.substr(len);
// solve subproblem
vector<string> segments = wordBreak(suffix,dict,cache);
for(int i = 0; i < segments.size(); ++i) {
if(segments[i].empty())
vs.push_back(prefix);
else
vs.push_back(prefix + " " + segments[i]);
}
}
}
cache[s] = vs;
return vs;
}
Edit Distance
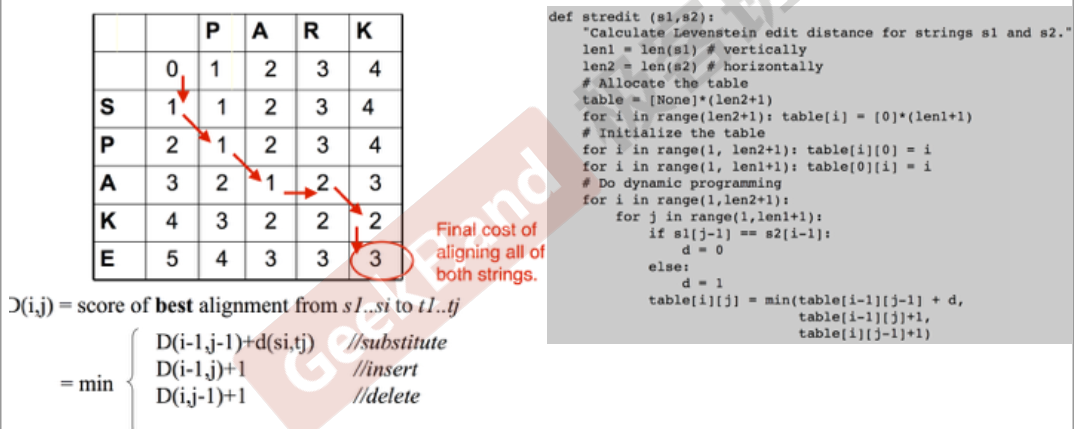
Summary
Sequence DP
- Climbing Stairs
- Jump game
- Palindrome Partitioning ii
- Word Break
- Triangle
- Longest Increasing Subsequence
- Max Subarray Sum
Two Sequences DP
- Coin Change
- Edit Distance
- LCS
Matrix DP
- Minimum Path Sum
- Triangle
- Unique Path I, II
Homework
Unique Binary Search Trees II (leetcode 95)
Given n, generate all structurally unique BST's (binary search trees) that store values 1...n.
For example, Given n = 3, your program should return all 5 unique BST's shown below.
Jump Game II (leetcode 45)
Given an array of non-negative integers, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Your goal is to reach the last index in the minimum number of jumps.
For example:
Given array A = [2,3,1,1,4]
The minimum number of jumps to reach the last index is 2. (Jump 1 step from index 0 to 1, then 3 steps to the last index.)
