算法原理与实践（栈与队列）

　　Stack & Queue

　　大纲

　　1. Stack介绍
　　2. Queue介绍
　　3. 例题分析

　　Stack
　　A stack is a container of objects that are inserted and removed according to the last-in first-out (LIFO) principle
　　Operations: Push O(1), Pop O(1), Top O(1)

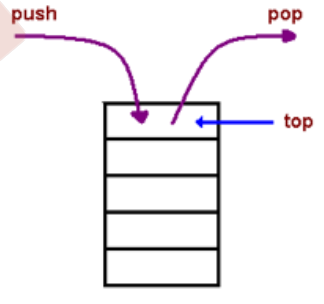
　　栈的用途
　　可以用 Stack 作为辅助，实现深度优先算法（Depth first search, DFS），或者将递归转为while循环
　　递归本身就是相当于把函数本身一层一层加到操作系统的内存栈上；入栈操作相当于递归调用自身，出栈操作相当于递归返回。

　　工具箱：C++
　　stack and queue:

bool empty() const; // Returns whether the stack is empty: i.e. whether its size is zero.
void push (const value_type& val); // Inserts a new element at the top of the stack. The content of this new element is initialized to a copy of val.
void pop(); // Removes the element on top of the stack, effectively reducing its size by one.
value_type& top(); // Returns a reference to the top element in the stack

　　Example:

stack<int> myStack;
myStack.push(10);
myStack.push(20);
int value = myStack.top(); // value equals to 20
queue<int> myQueue;
myQueue.push(10);
myQueue.push(20); // queue now has two elements, the value of which is 10, 20
int value = myQueue.front(); // value equals to 10
myQueue.pop(); // queue now has one element, the value of which is 20

　　

　　Queue
　　A queue is a container of objects (a linear collection) that are inserted and removed according to the first-in first-out (FIFO) principle
Operations: O(1) Push，O(1) Pop，O(1) Top
　　Always used for BFS

　　用途
　　我们可以用 Queue 作为辅助，实现广度优先算法（Breadth first search, BFS）
　　Queue 还可以作为 buffer，构建一个生产者－消费者模型：生产者把新的元素加到队尾，消费者从队头读取元素。在有两个线程同时读取同一个 queue 时，需要考虑同步（synchronization）
　　stack 与 queue 可以视作封装好的 Linked list，只是限制了访问和插入的自由。适用 stack 或 queue 的情境，也可以考虑使用更为强大的list。

　　模式识别
　　1. 通过stack实现特殊顺序的读取由于 stack 具有 LIFO 的特性，如需实现任何特定顺序的读取操作，往往可以借助两个 stack 互相”倾倒"来实现特定顺序。另一个stack作为辅助。

　　Get Max Stack
　　Implement a stack, enable O(1) Push, Pop Top, Max. Where Max() will return the value of maximum number in the stack.

　　解答
　　Using two stacks.
　　The first one is the regular stack. The second one only store maximum numbers if a larger number comes.
　　复杂度分析：时间复杂度符合题目要求为 O(1)。空间复杂度最坏情况附加的 stack 中需要储存每个元素，故额外使用O(n)空间。

　　代码实例

#include <stack>
#include <iostream>

using namespace std;

template<typename T>
class MaxStack
{
public:
    T top() const {
        return regulerS.top();
    }

    void pop() {
        if (!maxS.empty() && maxS.top() == regulerS.top()) {
            maxS.pop();
        }

        regulerS.pop();
    }

    void push(const T& val) {
        if (maxS.empty() || maxS.top() < val) {
            maxS.push(val);
        }

        regulerS.push(val);
    }

    T getMax() const {
        if (!maxS.empty()) {
            return maxS.top();
        }
        
        return regulerS.top();
    }

private:
    stack<T> regulerS;
    stack<T> maxS;
};

int main()
{
    MaxStack<int> ms;

    int arr[] = { 1,20,40,40,30,15,-5,50,45,16,22,24,28 };

    for (auto e : arr)
        ms.push(e);

    cout << ms.getMax() << endl;

    for (auto e : arr) {
        cout << ms.top() << "  " << ms.getMax() << endl;
        ms.pop();
    }

    return 0;
}

 

　　Queue using Stack

　　Implement a queue with stack structure.

#include <stack>
#include <iostream>

using namespace std;

template<typename T>
class Queue {
public:
    void push(const T& val) {
        s1.push(val);
    }

    T pop() {
        if (s1.empty())    return false;

        while (!s1.empty()) {
            s2.push(s1.top());
            s1.pop();
        }

        T val = s2.top();
        s2.pop();

        while (!s2.empty()) {
            s1.push(s2.top());
            s2.pop();
        }

        return val;
    }

    bool empty() const {
        return s1.empty();
    }
private:
    stack<T> s1;
    stack<T> s2;
};

int main(){
    Queue<int> q; 
    int arr[] = { 1,2,3,4 };

    for (auto e : arr) {
        q.push(e);
    }

    while (!q.empty()) {
        cout << q.pop() << " ";
    }

    return 0;
}

　　Sort Stack
　　How to sort a stack in ascending order (i.e. pop in ascending order) with another stack?
　　复杂度分析：由于调整一个元素的顺序可能要求将之前的n个元素来回倾倒，故时间复杂度O(n^2)。

#include <stack>
#include <iostream>

using namespace std;

template<typename T>
stack<T> sortStack(stack<T>& input) {
    stack<T> output;
    while (!input.empty()) {
        int val = input.top();
        input.pop();
        while (!output.empty() && output.top() < val) {
            input.push(output.top());
            output.pop();
        }
        output.push(val);
    }
    return output;
}

int main() {
    stack<int> s;
    int arr[] = { 3,2,1,4,5,6 };

    for (auto e : arr)
        s.push(e);

    s = sortStack(s);

    for (auto e : arr) {
        cout << s.top() << " ";
        s.pop();
    }

    return 0;
}

　　“save or later”问题
　　有一类问题有这样的特性：当前节点的解依赖后驱节点。对于某个当前节点，如果不能获知后驱节点，就无法得到有意义的解。这类问题可以通过stack（或等同于stack的若干个临时变量）解决：先将当前节点入栈，然后看其后继节点的值，直到其依赖的所有节点都完备时，再从栈中弹出该节点求解。某些时候，甚至需要反复这个过程：将当前节点的计算结果再次入栈，直到其依赖的后继节点完备。

　　Validate Parenthesis
　　Given a string containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is a valid parentheses string.
For example, “(([]))” is valid, but “(]” or “((” is not.

#include <iostream>
#include <string>
#include <stack>

using namespace std;

bool isMatch(const char lhs, const char rhs) {
    switch (lhs)
    {
    case '(':
        return rhs == ')' ? true : false;
    case '[':
        return rhs == ']' ? true : false;
    case '{':
        return rhs == '}' ? true : false;
    }
    return false;
}

bool validateParenthesis(const string str) {
    stack<char> st;

    for (unsigned int i = 0; i < str.length(); i++) {
        char c = str[i];
        if (!st.size()) {
            if(c == '}' || c == ']' || c == ')') {
                return false;
            }
            else {
                st.push(c);
            }
        } 
        else {
            if (isMatch(st.top(), c)) {
                st.pop();
            }
            else {
                st.push(c);
            }
        }
    }
    
    if (st.size())
        return false;
    else
        return true;
}

int main() {
    cout << validateParenthesis("]]") << endl;
    cout << validateParenthesis("(]") << endl;
    cout << validateParenthesis("(){}[]") << endl;
    cout << validateParenthesis("{[()]}") << endl;
    return 0;
}

 

　　模式匹配
　　3. 用 stack 解决 Top-Down 结构的问题
　　所谓的 Top-Down 结构，从逻辑理解的角度来看，实际上就是一种树形结构，从顶层出发，逐渐向下扩散，例如二叉树的周游问题。 在实际运算的时候，我们先解决子问题，再利用子问题的结果解决当前问题。
　　由于Stack的LIFO特性，可以利用Stack数据结构消除递归。Recursion 通常用函数调用自身实现，在调用的时候系统会分配额外的空间，并且需要用指针记录返回位置，故 overhead 比较大。

　　In-order Traversal（中序遍历）
　　Given a binary tree, implement the In-Order Traversal using a stack. The illustration of tree is in the below.

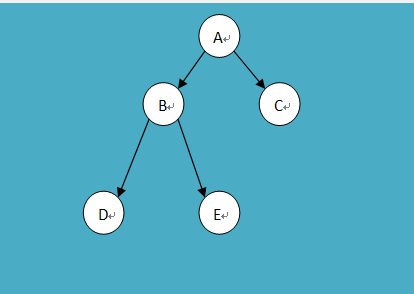
#include <iostream>
#include <stack>

using namespace std;

#define VALUE char

struct Node {
    Node(VALUE val) :val(val), left(nullptr), right(nullptr) {}
    VALUE val;
    struct Node* left;
    struct Node* right;
};

void inOrderTraversal(struct Node* const root) {
    stack<struct Node*> s;
    struct Node* p = root;

    while (!s.empty() || p){
        if (p) {
            s.push(p);
            p = p->left;
        }
        else {
            p = s.top();
            s.pop();
            cout << p->val << " ";
            p = p->right;
        }
    }
}

int main() {
    struct Node *root = new struct Node('A');
    root->left = new struct Node('B');
    root->left->left = new struct Node('D');
    root->left->right = new struct Node('E');
    root->right = new struct Node('C');

    inOrderTraversal(root);

    return 0;
}

 

　　Evaluate Expression
　　Inorder fix(4 + 5) * (7 - 2)
　　Postfix Expression : 4 5 + 7 2 - *

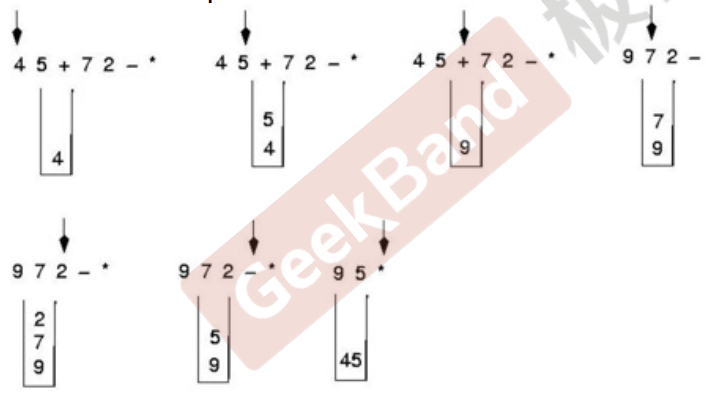
#include <iostream>
#include <string>
#include <stack>
#include <queue>

using namespace std;

 queue<char> inOrder2Postfix(const string inOrderExpression) {
    stack<char> operatorStack;
    queue<char> postfixExpression;

    for (string::size_type i = 0; i < inOrderExpression.length(); i++) {
        char c = inOrderExpression[i];

        switch (c)
        {
        case '+':
        case '-':
            while (operatorStack.top() == '*' || operatorStack.top() == '/' 
                || operatorStack.top() == '+' || operatorStack.top() == '-') 
            {
                postfixExpression.push(operatorStack.top());
                operatorStack.pop();
            }
            operatorStack.push(c);
            break;
        case '*':
        case '/':    //if top() > currentOperator then pop()
            if (operatorStack.empty()) {
                operatorStack.push(c);
                break;
            }

            if (operatorStack.top() == '+' || operatorStack.top() == '-') {
                operatorStack.push(c);
                break;
            }
            
            if(operatorStack.top() == '(') {
                operatorStack.push(c);
                break;
            }
            
            if (operatorStack.top() == '*' || operatorStack.top() == '/') {
                postfixExpression.push(operatorStack.top());
                operatorStack.pop();
                operatorStack.push(c);
                break;
            }
            
        case '(':
            operatorStack.push(c);
            break;
        case ')':
            while (operatorStack.top() != '(') {
                postfixExpression.push(operatorStack.top());
                operatorStack.pop();
            }
            
            if (operatorStack.top() == '(')
                operatorStack.pop();

            break;
        default:    //digital
            postfixExpression.push(c);
            break;
        }
    }

    while (!operatorStack.empty()) {
        postfixExpression.push(operatorStack.top());
        operatorStack.pop();
    }

    return postfixExpression;
}

double evaluateExpression(const string expression) {
    queue<char> postfixExpression = inOrder2Postfix(expression); //先将中缀转化为后缀
    stack<double> number;

    double lhs = 0;
    double rhs = 0;

    while (!postfixExpression.empty()) {
        char c = postfixExpression.front();
        postfixExpression.pop();
        switch (c)
        {
        case '+':
            rhs = number.top(); 
            number.pop();
            lhs = number.top();
            number.pop();
            number.push(lhs + rhs);
            break;
        case '-':
            rhs = number.top();
            number.pop();
            lhs = number.top();
            number.pop();
            number.push(lhs - rhs);
            break;
        case '*':
            rhs = number.top();
            number.pop();
            lhs = number.top();
            number.pop();
            number.push(lhs * rhs);
            break;
        case '/':
            rhs = number.top();
            number.pop();
            lhs = number.top();
            number.pop();
            number.push(lhs / rhs);
            break;
        default:
            number.push(c - 48);
            break;
        }
    }

    return number.top();
}

int main() {
    string s = "(4+5)*(7-2)";
    double result = evaluateExpression(s); 
    cout << result << endl;

    s = "4*5/7";
    result = evaluateExpression(s);
    cout << result << endl;

    return 0;
}

 

　　Extension
　　How to calculate
　　3 + 14 * 5
　　(12 + 3) * (3 + 2) ^ 2

　　以下程序是可以计算多位数乘方和幂运算的程序。

#include <iostream>
#include <string>
#include <vector>
#include <map>
#include <stack>
#include <sstream>
#include <cmath>

using namespace std;

#define OP 1
#define NUM 2

#define ADD "+"
#define SUB "-"
#define MUL "*"
#define DIV "/"

#define LONG 21
#define DOUBLE 22


struct Word {
    Word(const string word) : val(word) {
        if (word == "+" || word == "-" || word == "*" || word == "/" || word == "(" || word == ")" || word == "^") {
            type = OP;
        }
        else {
            type = NUM;
        }
    }
    int type;
    string val;
    const map<const string, int> m = {
        { "(", 1 },
        { "+", 2 },
        { "-", 2 },
        { "*", 3 },
        { "/", 3 },
        { "^", 3 }
    };
};

bool operator==(const Word &lhs, const int rhs) {
    return lhs.type == rhs;
}

bool operator> (const Word &lhs, const Word &rhs) {
    if (lhs.type == OP && rhs.type == OP) {
        return lhs.m.at(lhs.val) - rhs.m.at(rhs.val) >= 0 ? true : false;
    }
    return false;
}

bool operator== (const Word &lhs, const string rhs) {
    return lhs.val == rhs;
}

vector<Word> inorder2Postorder(const vector<Word> &v) {
    stack<Word> st;

    vector<Word> postfix;

    vector<Word>::const_iterator it = v.cbegin();
    while (it != v.cend()) {
        if (*it == NUM) {
            postfix.push_back(it++->val);
            continue;
        }
        if (*it == "(") {
            st.push(*it++);
            continue;
        }
        if (*it == ")") {
            while (!st.empty() && st.top().val != "(") {
                postfix.push_back(st.top());
                st.pop();
            }
            st.pop();
            it++;
            continue;
        }
        while (!st.empty() && st.top() > *it) {
            postfix.push_back(st.top());
            st.pop();
        }

        st.push(*it++);
    }

    while (!st.empty()) {
        postfix.push_back(st.top().val);
        st.pop();
    }

    return postfix;
}

vector<Word> str2Words(const string &exp) {
    string::const_iterator it = exp.cbegin();
    string line;

    while (it != exp.cend()) {
        if (*it == '+' ||
            *it == '-' ||
            *it == '*' ||
            *it == '/' ||
            *it == '(' ||
            *it == ')' ||
            *it == '^')
        {
            line += " ";
            line += *it;
            line += " ";
        }
        else {
            line += *it;
        }
        it++;
    }

    vector<Word> v;
    istringstream iss(line);
    string word;
    while (iss >> word) {
        v.push_back(word);
    }

    return v;
}

double calculatePostfix(const vector<Word> v) {
    vector<Word>::const_iterator it = v.cbegin();
    stack<double> st;
    double lhs, rhs;

    while (it != v.cend()) {
        if (*it == "*") {
            rhs = st.top(); st.pop();
            lhs = st.top(); st.pop();
            lhs = lhs * rhs;
            st.push(lhs);
        }
        else if (*it == "/") {
            rhs = st.top(); st.pop();
            lhs = st.top(); st.pop();
            lhs = lhs / rhs;
            st.push(lhs);
        }
        else if (*it == "+") {
            rhs = st.top(); st.pop();
            lhs = st.top(); st.pop();
            lhs = lhs + rhs;
            st.push(lhs);
        }
        else if (*it == "-") {
            rhs = st.top(); st.pop();
            lhs = st.top(); st.pop();
            lhs = lhs - rhs;
            st.push(lhs);
        }
        else if (*it == "^") {
            rhs = st.top(); st.pop();
            lhs = st.top(); st.pop();
            lhs = pow(lhs, rhs);
            st.push(lhs);
        }
        else {
            if (it->val.find(".") == string::npos) {
                st.push(atol(it->val.c_str()));
            }
            else {
                st.push(atof(it->val.c_str()));
            }
        }
        it++;
    }
    
    return st.top();
}

int main() {
    string exp;
    vector<Word> inorderExp;
    vector<Word> postfix;

    //exp = "4+3*(2.5+1)";
    //inorderExp = str2Words(exp);
    //postfix = inorder2Postorder(inorderExp);
    //cout << calculatePostfix(postfix) << endl;

    //exp = "3+14*5";
    //inorderExp = str2Words(exp);
    //postfix = inorder2Postorder(inorderExp);
    //cout << calculatePostfix(postfix) << endl;

    exp = "(3+2)^2*(12+3)";
    inorderExp = str2Words(exp);
    postfix = inorder2Postorder(inorderExp);
    cout << calculatePostfix(postfix) << endl;

    return 0;
}

 

 

　　Queue扩展
　　1. Circles Queue

　　循环队列
　　2. Queue with Max

　　Implement a queue, enable O(1) Push, Pop Top, Max. Where Max() will return the value of maximum number in the queue.
　　3. PriorityQueue

　　从严格的意义上讲，优先队列其实是一个堆。堆的实现方式有四种。 1，基于简单链表；2，基于二叉查找树；3，基于完全二叉树；4基于完全二叉树的数组实现。

　　4. Blocking Queue(Multi - thread)

　　BlockingQueue, 如果BlockQueue是空的, 从BlockingQueue取东西的操作将会被阻断进入等待状态, 直到BlockingQueue进了东西才会被唤醒.同样, 如果BlockingQueue是满的, 任何试图往里存东西的操作也会被阻断进入等待状态, 直到BlockingQueue里有空间才会被唤醒继续操作.

　　

　　Homework
　　Queue with Max

　　解题代码如下：

#include <iostream>
#include <queue>
#include <initializer_list>

using namespace std;

template<typename T>
class QueueWithMax {
public:
    QueueWithMax(initializer_list<T> il) {
        for (auto e : il)
            this->push(e);
    }

    void push(const T &val) {
        if (mq.empty() || mq.back() < val) {
            mq.push(val);
        }
        rq.push(val);
    }

    void pop() {
        if (rq.front() == mq.front()) {
            mq.pop();
        }
        rq.pop();
    }

    T max() {
        if (!mq.empty())
            return mq.back();
        else if (rq.empty())
            return rq.front();
        else
            return NULL;
    }

    T front() {
        return rq.front();
    }

private:
    queue<T> rq;
    queue<T> mq;
};

int main() {
    QueueWithMax<int> qwm = { 1,2,5,3,4 };

    cout << qwm.front() << endl;
    cout << qwm.max() << endl;

    return 0;
}

 

　　Evaluate(3 + 4) * 14

　　解题代码如下：

#include <iostream>
#include <string>
#include <vector>
#include <map>
#include <stack>
#include <sstream>
#include <cmath>

using namespace std;

#define OP 1
#define NUM 2

#define ADD "+"
#define SUB "-"
#define MUL "*"
#define DIV "/"

#define LONG 21
#define DOUBLE 22


struct Word {
    Word(const string word) : val(word) {
        if (word == "+" || word == "-" || word == "*" || word == "/" || word == "(" || word == ")" || word == "^") {
            type = OP;
        }
        else {
            type = NUM;
        }
    }
    int type;
    string val;
    const map<const string, int> m = {
        { "(", 1 },
        { "+", 2 },
        { "-", 2 },
        { "*", 3 },
        { "/", 3 },
        { "^", 3 }
    };
};

bool operator==(const Word &lhs, const int rhs) {
    return lhs.type == rhs;
}

bool operator> (const Word &lhs, const Word &rhs) {
    if (lhs.type == OP && rhs.type == OP) {
        return lhs.m.at(lhs.val) - rhs.m.at(rhs.val) >= 0 ? true : false;
    }
    return false;
}

bool operator== (const Word &lhs, const string rhs) {
    return lhs.val == rhs;
}

vector<Word> inorder2Postorder(const vector<Word> &v) {
    stack<Word> st;

    vector<Word> postfix;

    vector<Word>::const_iterator it = v.cbegin();
    while (it != v.cend()) {
        if (*it == NUM) {
            postfix.push_back(it++->val);
            continue;
        }
        if (*it == "(") {
            st.push(*it++);
            continue;
        }
        if (*it == ")") {
            while (!st.empty() && st.top().val != "(") {
                postfix.push_back(st.top());
                st.pop();
            }
            st.pop();
            it++;
            continue;
        }
        while (!st.empty() && st.top() > *it) {
            postfix.push_back(st.top());
            st.pop();
        }

        st.push(*it++);
    }

    while (!st.empty()) {
        postfix.push_back(st.top().val);
        st.pop();
    }

    return postfix;
}

vector<Word> str2Words(const string &exp) {
    string::const_iterator it = exp.cbegin();
    string line;

    while (it != exp.cend()) {
        if (*it == '+' ||
            *it == '-' ||
            *it == '*' ||
            *it == '/' ||
            *it == '(' ||
            *it == ')' ||
            *it == '^')
        {
            line += " ";
            line += *it;
            line += " ";
        }
        else {
            line += *it;
        }
        it++;
    }

    vector<Word> v;
    istringstream iss(line);
    string word;
    while (iss >> word) {
        v.push_back(word);
    }

    return v;
}

double calculatePostfix(const vector<Word> v) {
    vector<Word>::const_iterator it = v.cbegin();
    stack<double> st;
    double lhs, rhs;

    while (it != v.cend()) {
        if (*it == "*") {
            rhs = st.top(); st.pop();
            lhs = st.top(); st.pop();
            lhs = lhs * rhs;
            st.push(lhs);
        }
        else if (*it == "/") {
            rhs = st.top(); st.pop();
            lhs = st.top(); st.pop();
            lhs = lhs / rhs;
            st.push(lhs);
        }
        else if (*it == "+") {
            rhs = st.top(); st.pop();
            lhs = st.top(); st.pop();
            lhs = lhs + rhs;
            st.push(lhs);
        }
        else if (*it == "-") {
            rhs = st.top(); st.pop();
            lhs = st.top(); st.pop();
            lhs = lhs - rhs;
            st.push(lhs);
        }
        else if (*it == "^") {
            rhs = st.top(); st.pop();
            lhs = st.top(); st.pop();
            lhs = pow(lhs, rhs);
            st.push(lhs);
        }
        else {
            if (it->val.find(".") == string::npos) {
                st.push(atol(it->val.c_str()));
            }
            else {
                st.push(atof(it->val.c_str()));
            }
        }
        it++;
    }
    
    return st.top();
}

int main() {
    string exp;
    vector<Word> inorderExp;
    vector<Word> postfix;

    //exp = "4+3*(2.5+1)";
    //inorderExp = str2Words(exp);
    //postfix = inorder2Postorder(inorderExp);
    //cout << calculatePostfix(postfix) << endl;

    //exp = "3+14*5";
    //inorderExp = str2Words(exp);
    //postfix = inorder2Postorder(inorderExp);
    //cout << calculatePostfix(postfix) << endl;

    exp = "(3+2)^2*(12+3)";
    inorderExp = str2Words(exp);
    postfix = inorder2Postorder(inorderExp);
    cout << calculatePostfix(postfix) << endl;

    return 0;
}

 

<End>