树（Heap）

　　对于大量的输入数据，链表的线性访问时间太慢，不宜使用——《数据结构与算法分析——C 语言描述》 p 65

　　对于大量的输入数据，适合用树结构，大部分操作都是 O( log N )。

　　二叉树

　　1. 实现

　　节点定义

template<typename T>
struct Node
{
    Node(T v) : val(v), left(nullptr), right(nullptr) {};

    T val;
    struct Node *left;
    struct Node *right;
};

　　构建树并添加节点

　　按照如图的树构建

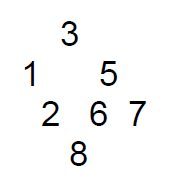
Node<int> *root = new Node<int>(3); //根节点

root->left = new Node<int>(1); //根节点的左子树
root->left->right = new Node<int>(2);

root->right = new Node<int>(5); //根节点的又子树
root->right->left = new Node<int>(6);
root->right->left->left = new Node<int>(8);
root->right->right = new Node<int>(7);

　　遍历

　　递归方式

template<typename T>
void traversalRecursion(const struct Node<T>* const p)
{
    if (p != nullptr)
    {
        cout << p->val;

        traversalRecursion(p->left);
        traversalRecursion(p->right);
    }
    else
        cout << "#";
}

　　非递归方式——用栈消除递归

template<typename T>
void traversalStack(struct Node<T> *const root)
{
    stack<struct Node<T>*> s;

    s.push(root);

    while (s.size())
    {
        struct Node<T> *const p = s.top();

        s.pop();

        if (p == nullptr)
        {
            cout << "#";
            continue;
        }

        cout << p->val;

        s.push(p->right);
        s.push(p->left);
    }
}

　　表达式树

　　后缀表达式：　　a b + c d e + * *

　　从“后缀表达式”开始构造一颗表达式树，仅类定义

template<typename T>
class ExpressionTree
{
public:
    struct Node<T>* initFormPostfix(const string &postfix)
    {
        istringstream iss(postfix);
        T c;

        while (iss >> c)
        {
            struct Node<T> *const p = new struct Node<T>(c);

            switch (characterType(c))
            {
            case 0:    
                sk.push(p);
                break;

            case 1:
                p->right = sk.top(); sk.pop();
                p->left = sk.top(); sk.pop();
                
                sk.push(p);
                break;
            }
        }

        return sk.top();
    }

private:
    int characterType(const T &c) const
    {
        if (c == "+" || c == "-"  || c == "*" || c == "/")
            return 1;

        return 0;
    }

    stack<struct Node<T>*> sk;
};

 　　完整代码

#include <iostream>
#include <string>
#include <sstream>
#include <stack>
#include <memory>

using namespace std;

template<typename T>
struct Node
{
    Node(T v) : val(v), left(nullptr), right(nullptr) {};
    T val;
    struct Node *left;
    struct Node *right;
};

template<typename T>
class ExpressionTree
{
public:
    struct Node<T>* initFormPostfix(const string &postfix)
    {
        istringstream iss(postfix);
        T c;

        while (iss >> c)
        {
            struct Node<T> *const p = new struct Node<T>(c);

            switch (characterType(c))
            {
            case 0:    
                sk.push(p);
                break;

            case 1:
                p->right = sk.top(); sk.pop();
                p->left = sk.top(); sk.pop();
                
                sk.push(p);
                break;
            }
        }

        return sk.top();
    }

private:
    int characterType(const T &c) const
    {
        if (c == "+" || c == "-"  || c == "*" || c == "/")
            return 1;

        return 0;
    }

    stack<struct Node<T>*> sk;
};

template<typename T>
void traversalRecursion(const struct Node<T>* const p)
{
    if (p != nullptr)
    {
        cout << p->val;

        traversalRecursion(p->left);
        traversalRecursion(p->right);
    }
    else
        cout << "#";
}

int main()
{
    string postfix = "a b + c d e + * *";

    ExpressionTree<string> et;

    const struct Node<string> *root = et.initFormPostfix(postfix);

    traversalRecursion(root);

    return 0;
}

　　二叉查找树

　　构建

　　构建如图所示的二叉查找树

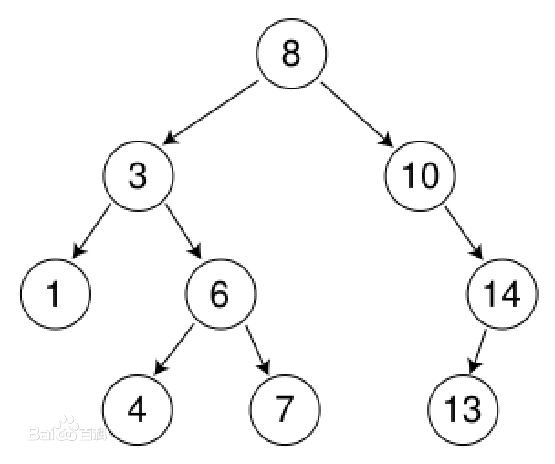
　　构建 + 遍历 代码如下

#include <iostream>
#include <initializer_list>
#include <stack>

using namespace std;

template<typename T>
struct Node
{
    Node(T v) : val(v), left(nullptr), right(nullptr) {}
    T val;
    struct Node* left;
    struct Node* right;
};

template<typename T>
class BinarySearchTree
{
public:
    BinarySearchTree()
    {
        root = new struct Node<T>(0);
    }

    BinarySearchTree(const initializer_list<T> il) : BinarySearchTree()
    {
        initializer_list<T>::iterator it = il.begin();

        root->val = *it++;

        while (it != il.end())
            insert(*it++);
    }

    void insert(const T &val)
    {
        struct Node<T> **p = &root;

        while (*p != nullptr)
        {
            if (val == (*p)->val)
                return;

            if (val < (*p)->val)
            {
                p = &((*p)->left);
                continue;
            }

            if (val > (*p)->val)
            {
                p = &((*p)->right);
                continue;
            }
        }

        *p = new struct Node<T>(val);
    }

    void traversalStack()
    {
        stack<struct Node<T>*> s;

        s.push(root);

        while (s.size())
        {
            struct Node<T> *const p = s.top();

            s.pop();

            if (p == nullptr)
            {
                cout << "#";
                continue;
            }

            cout << p->val;

            s.push(p->right);
            s.push(p->left);
        }
    }

private:
    struct Node<T> *root;
};

int main(void)
{
    BinarySearchTree<int> bst({ 8, 3, 10, 1, 6, 14, 4, 7, 13 });

    bst.traversalStack();

    return 0;
}

 　　查找 代码如下

struct Node<T>* find(const T &val) const
{
    struct Node<T> *p = root;

    while (p != nullptr)
    {
        if (p->val == val)
            return p;

        if (val < p->val)
            p = p->left;

        if (val > p->val)
            p = p->right;
    }

    return nullptr;
}

　　 树的遍历

　　后序遍历

　　利用后序遍历求树的深度

unsigned getBinaryTreeHeigt(const struct Node *const p)
{
    if (p == nullptr)
        return -1;
    else
        return 1 + max(getBinaryTreeHeigt(p->left), getBinaryTreeHeigt(p->right));
}

　　层序遍历

　　代码一，非递归实现

void levelOrderTraversal(struct Node *root)
{
    queue<struct Node*> q;

    q.push(root);

    while (q.size())
    {
        struct Node *p = q.front();

        q.pop();

        if (p == nullptr)
            continue;

        q.push(p->left);
        q.push(p->right);

        cout << p->val << " ";
    }
}

　　代码二，递归实现

void levelVisit(queue<struct Node*> &que) {
    if (que.empty())    return;

    struct Node *p = que.front();    que.pop();

    if (p == nullptr)    return;

    cout << p->val << " ";

    que.push(p->left);
    que.push(p->right);

    levelVisit(que);
}

 

　　利用队列可以完成二叉树的层序遍历（广度优先遍历）；利用栈可以完成二叉树的深度优先遍历。