牛客网提高组模拟赛第七场 T2 随机生成树
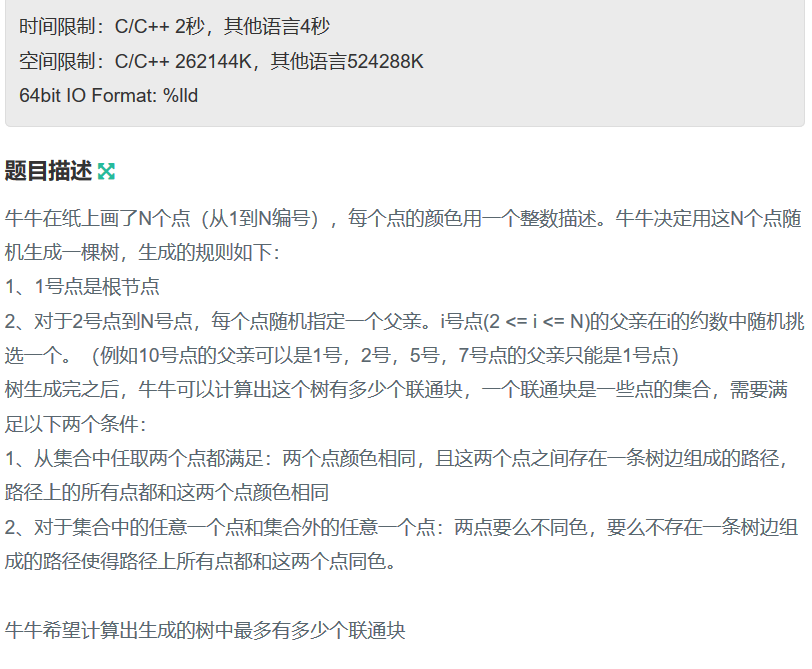
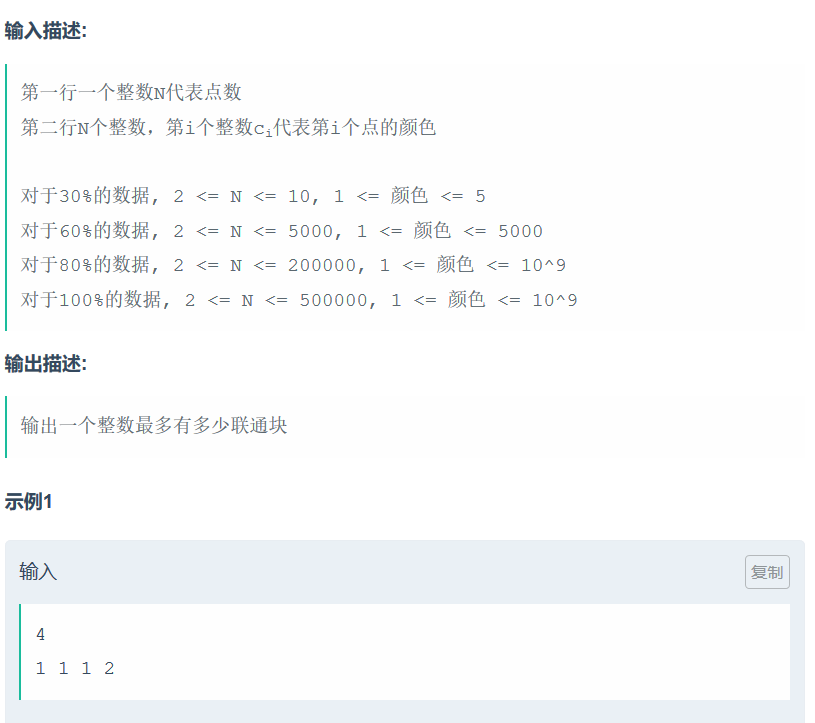
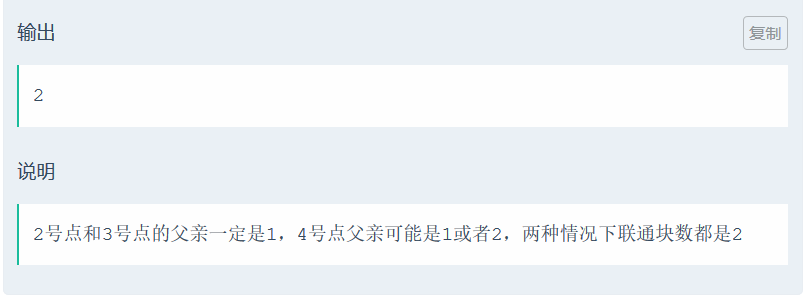
其实看懂题就很水啦qwq,就是求\(1-N\)的约数啦。
暴力求的话时间复杂度是\(O(NlogN)\)的,其实正解是枚举每个数的倍数......这样的时间复杂度是\(\frac{N}{1}+\frac{N}{2}+...+\frac{N}{N}\)的,由于调和级数可以看做\(O(log)\),所以总复杂度为\(O(NlogN)\)。
但是比赛的时候我写的是那个复杂度很劣的做法,所以。。。。代码就先放这个了。。(注意%运算是真的慢。。。。)
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#define MAXN 500010
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
}
int n,ans=1;
int c[MAXN];
int main()
{
n=read();
for(int i=1;i<=n;i++) c[i]=read();
for(int i=1;i<=n;i++)
{
for(int j=1;j*j<=i;j++)
{
if(i%j) continue;
if(c[j]!=c[i]||c[i/j]!=c[i])
{
ans++;
break;
}
}
}
printf("%d\n",ans);
return 0;
}


