OI数学 简单学习笔记
基本上只是整理了一下框架QAQ
PART1 数论部分
最大公约数
对于正整数x,y,最大的能同时整除它们的数称为最大公约数
常用的:\(lcm(x,y)=xy\gcd(x,y)\)
裴蜀定理
定理:对于方程\(ax+by=c\),其存在解的充要条件是\(gcd(a,b)|c\),可以拓展到n元的方程。
证明的话应该自己yy一下还是很容易(显然可得),不过要是想要严谨证明还是去百度吧qwq
扩展欧几里得定理
首先我们都知道\(gcd(a,b)=gcd(b,a \%b)\)吧。
我们在辗转相除的同时可以递归地求出\(ax+by=gcd(a,b)\)的解。当递归到b=0的时候,显然有解\(x=1,y=0\)。如果b!=0,我们可以递归的求出\(bx'+(a\%b)y'=gcd(a,b)\)的解。
所以\(x=y',y=(x'- \lfloor \frac{a}{b} \rfloor y')\)
时间复杂度:O(log n)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define MAXN 100010
using namespace std;
int n,p;
inline void exgcd(int a,int b,int &x,int &y)
{
if(b==0) {x=1,y=0;return;}
else
{
int tx,ty;
exgcd(b,a%b,tx,ty);
x=ty;
y=tx-(a/b)*ty;
return;
}
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("ce.in","r",stdin);
#endif
scanf("%d%d",&n,&p);
for(int i=1;i<=n;i++)
{
int x,y;
exgcd(i,p,x,y);
while(x<0) x+=p;
printf("%d\n",x);
}
return 0;
}
逆元
定义:
若有\(xy=1\pmod p\),则称y为x模p意义下的乘法逆元
计算方法:
转换为方程:\(xy-kp=1\),用拓展欧几里得算法就可以了。当然费马小定理也可以,只不过时间复杂度上稍微逊色一些。(还有一种线性的,不过我不会)
补充:费马小定理:若p为质数,对于任意\(1<=a<p,a^{p-1}\equiv 1 \pmod p\),那么在p为质数的时候\(a^{p-2}就是a的逆元\)
对于费马小定理的补充:\(a^b\equiv a^{b\%(p-1)}\pmod p\)
欧拉筛(线性筛)
在埃氏筛法的基础上,让每个合数只被它的最小质因子筛选一次,以达到不重复的目的。
模板:
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#define MAXN 10000010
using namespace std;
int cnt,n,m;
int not_prime[MAXN],prime[MAXN];
inline void init(){
not_prime[1]=1;
for(int i=2;i<=MAXN;i++){
if(not_prime[i]==0){
prime[++cnt]=i;
}
for(int j=1;j<=cnt&&prime[j]*i<=MAXN-10;j++){
not_prime[prime[j]*i]=1;
if(i%prime[j]==0) break;
}
}
}
int main(){
#ifndef ONLINE_JUDGE
freopen("ce.in","r",stdin);
#endif
scanf("%d%d",&m,&n);
init();
while(n--){
int a;
scanf("%d",&a);
if(not_prime[a]==0) printf("Yes\n");
else printf("No\n");
}
return 0;
}
不过有一组性质,下面会提到(在约数个数和那里)
积性函数
对于任意互质整数a,b,存在\(f(ab)=f(a)f(b)\)性质的数论函数。
(积性函数的卷积仍然是积性函数)
完全积性函数则是没有互质的限制。
常见的积性函数举例:
- φ(n) -欧拉函数
- μ(n) -莫比乌斯函数,关于非平方数的质因子数目 \(μ(n)=[k_1\le1][k_2\le1]...[k_m\le1](-1)^m\)
- gcd(n,k) -最大公因子,当k固定的情况
- d(n) -n的正因子数目
- \(σ_k(n)\) -n的所有正因子的k次方之和(0次方的时候就是所有因子和了)\(σ_k(n)=n*\frac{p1-1}{p1}...\frac{p_m-1}{p_m}\)
积性函数都可以用线性筛筛出来
欧拉函数
定义:\(\phi(n)\)定义为1-n内与n互质的数的个数
\(\phi(x)=x\prod_1^n(1- \frac{1}{p_i})\),其中x是正整数,\(p_i\)是x的质因数。
这个的计算程序十分好写。
特别的,欧拉函数是积性函数,即 \(\phi(mn)=\phi(m)\phi(n)\)。
证明比较显然。
这个样子是可以用线性筛,用线性的时间复杂度筛出来欧拉函数的答案——
那么φ(1)=1,n为质数时φ(n)=n−1,最小质因子筛到它时乘上质因子p−1,否则乘上这个质数
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define MAXN 110
using namespace std;
int cnt;
int not_prime[MAXN],phi[MAXN],prime[MAXN];
inline void solve()
{
for(int i=2;i<MAXN;i++)
{
if(!not_prime[i])
{
prime[++cnt]=i;
phi[i]=i-1;
}
for(int j=1;j<=cnt&&i*prime[j]<MAXN;j++)
{
not_prime[i*prime[j]]=1;
if(i%prime[j]==0)
{
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
else phi[i*prime[j]]=phi[i]*(prime[j]-1);
}
}
}
int main()
{
solve();
for(int i=1;i<=36;i++) printf("phi[%d]=%d\n",i,phi[i]);
return 0;
}
线性求逆元
在模p意义下求i的逆元:
\(p=i*x+y\)
那么\(i*x+y\equiv0\pmod p\)
两边除以\(ij\)
\(x*j^{-1}+i^{-1}\equiv0\pmod p\)
\(i^{-1}\equiv-x*j^{-1}\pmod p\)
inv[1]=1;
for(int i=2;i<=n;i++)
inv[i]=1ll*(p-p/i)*inv[p%i]%p;
阶乘逆元的递推
其实把最后的那个\(inv[i]\)求出来,然后逆着一路乘上来就行了。
约数个数的递推
学习来源
理论基础:
1、对n质因数分解,\(n=p1^k1 * p2^k2 * p3^k3\) ……
则n的约数个数为\((k1+1)*(k2+1)*(k3+1)\)……
2、线性筛素数时,用i和素数pj来筛掉 i*pj,
其中pj一定是i*pj的最小素因子
如果i是pj的倍数,pj也是i的最小素因子
设\(t[i]\) 表示i的约数个数,\(e[i]\) 表示i的最小素因子的个数
A、如果i是质数,\(t[i]=2,e[i]=1\)
B、如果i不是质数,枚举已有的质数\(p_j\)
i*pj的最小素因子是pj
1、如果i是pj的倍数那么e[i]即为i中包含的pj的个数,所以i*pj中包含的pj的个数为\(e[i]+1\)
所以\(e[i*pj]=e[i]+1,t[i*pj]=t[i]/(e[i]+1)*(e[i]+2)\)
2、如果i不是pj的倍数
\(e[i*pj]=1,t[i*pj]=t[i]*t[pj]\)(积性函数的性质)
\(=t[i]*2\)(素数的约数个数=2)
inline void init()
{
memset(is_prime,1,sizeof(is_prime));
is_prime[1]=0,mu[1]=1,d[1]=1;
for(int i=2;i<=limit;i++)
{
if(is_prime[i]) prime[++cnt]=i,e[i]=1,d[i]=2,mu[i]=-1;
for(int j=1;j<=cnt&&i*prime[j]<=limit;j++)
{
is_prime[i*prime[j]]=0;
e[i*prime[j]]=1;
if(i%prime[j]==0)
{
e[i*prime[j]]+=e[i];
mu[i*prime[j]]=0;
d[i*prime[j]]=d[i]*(e[i*prime[j]]+1)/e[i*prime[j]];
break;
}
mu[i*prime[j]]=-mu[i];
d[i*prime[j]]=d[i]*2;
}
}
}
线性筛约数和
\(t[i]\) 表示i的约数和
\(e[i]\) 表示i的约数中,不能被i的最小素因子整除的约数和
A、i是质数,\(t[i]=i+1,e[i]=1\)
B、i不是质数
\(i*pj\)的最小素因子是\(pj\)
1、如果i不是pj的倍数,那么i的所有约数中,必然没有pj的倍数
可以用反证法证明这个:设x是i的约数,且x是pj的倍数,
那么\(x=pj*b,i=x*a=pj*b*a\)
即i是pj的b*a倍,与i不是pj的倍数相矛盾
令S表示i的约数集,S’表示i的约数翻pj倍后的数的集合
则S∩S’=∅,则S和S’中无重复元素
所以\(t[i*pj]=S+S'=t[i]+t[i]*pj=t[i]*(pj+1)\)
S’中的所有元素都能整除pj,所以\(e[i*pj]=t[i]\)
2、如果i是pj的倍数,那么S和S’必有交集T
T=S中pj的倍数
所以\(i*pj\)的约数和要去除交集T
那么\(t[i*pj]=S+S'-T=S'+S-T=t[i]*pj+e[i]\)
因为pj既是i的最小素因子,又是\(i*pj\)的最小素因子
所以\(e[i*pj]=e[i]\)
isprime[1]=1;
for(int i=2;i<=n;i++)
{
if(!isprime[i])
{
prime[++num]=i;
t[i]=i+1;
e[i]=1;
}
for(int j=1;j<=cnt&&i*prime[j]<=n;j++)
{
isprime[i*prime[j]]=1;
if(i%prime[j]==0)
{
t[i*prime[j]]=t[i]*prime[j]+e[i];
e[i*prime[j]]=e[i];
break;
}
else
{
t[i*prime[j]]=t[i]*(prime[j]+1);
e[i*prime[j]]=t[i];
}
}
}
欧拉定理&扩展欧拉定理
欧拉定理——需要\(a,m\)互质:$$a^{\phi(m)}\equiv1\pmod m$$
拓展欧拉定理——
证明请看这篇博客 戳我
Miller-Rabin素性测试
因为当p为质数且\(1<=a<p\)时,\(a^{p-1}\equiv 1\pmod p\)(欧拉定理)
那么当\(1\le a<p\)且\(a^{p-1}\equiv 1\pmod p\)时,p是否一定是质数呢?
当然不是啦!但是我们发现大部分合数都不满足这个性质。
所以我们的素数判定算法出世啦!随机几个a,判断\(a^{p-1}\mod p\)是否为1——不过这个正确性有点玄学,因为有些合数对任意的a的也都满足这个性质emmmmm,所以需要对算法进行改进。
这样就引出了我们的二次探测定理——
在进行Miller-rabbin算法之前,先筛去偶数,接下来只需要对奇数进行判断。
于素数p而言,任意x=1,...,p-1,都有\(x^p\equiv x\pmod p\),而于合数,这个等式不一定成立。根据这个性质,如果找到了\(1\le x<n\)且不满足\(x^n\equiv x\pmod n\),说明这个数n一定是合数。
然而存在一些Carmichael数(比如说561),虽然是合数,但x取遍1,...,n-1都满足\(x^n\equiv \pmod n\)
考虑\(x^2\equiv 1\pmod n\)的根,如果n是奇素数,只有1和n-1两根:若n是奇合数,一定存在其他的根。
设\(n-1=2^r*d\),其中d是奇数。若存在\(0\le k<r\),\(a^{2^k*d}\)不同余1或-1(mod n),但是\(a^{2^{k+1}*d}\equiv1 \pmod n\),可推断n一定是合数。
算法时间复杂度是log的。
加上这个玄学改进,如果我们随机的a够多,几乎就卡不掉了。随机k个判断错误的概率仅有\(\frac{1}{2^k}\)。
对于int32范围内的数,使用2,7,61探测即可。对于int64范围内的数,使用前10个素数作为探测基底即可保证算法成功。
Pollard-Rho大整数质因数分解算法
听说没有什么大用qwq???蒟蒻选择战略性放弃
中国剩余定理(CRT)
void exgcd(int a,int b,int &x,int &y)
{
if(b==0){ x=1; y=0; return;}
exgcd(b,a%b,x,y);
int tp=x;
x=y; y=tp-a/b*y;
}
int china()
{
int ans=0,lcm=1,x,y;
for(int i=1;i<=k;++i) lcm*=b[i];
for(int i=1;i<=k;++i)
{
int tp=lcm/b[i];
exgcd(tp,b[i],x,y);
x=(x%b[i]+b[i])%b[i];//x要为最小非负整数解
ans=(ans+tp*x*a[i])%lcm;
}
return (ans+lcm)%lcm;
}
exCRT
咕咕
BSGS
bsgs就是哈希表(或map)+分块结合起来的优美算法。
一般用来解决求\(a^x\equiv y\pmod p\)有解的(最小)x。
一般我们令\(x=i*m-j\),(如果向别人那样写\(x=i*m+j\)到最后是需要exgcd的)。其中\(m=\sqrt p\)(因为这样时间复杂度最优,总体时间复杂度即\(O(\sqrt p)\))
然后有\(a^{im-j}\equiv y\pmod p\)
\(a^{im}\equiv y*a^j\pmod p\)
之后我们枚举j(\(j\in[0,m-1]\)),把右边的值塞进哈希表里面(或者map也行)。
for(int i=0,t=z;i<m;t=1ll*t*y%p,i++) M[t]=i;
最后枚举i看看哈希表里有没有原先已经塞进去的值了。如果有,就输出\(im-j\)即可。
for(int i=1,tt=pow(y,m),t=tt;i<m;i++,t=1ll*tt*t%p)
if(M.count(t)) {printf("%d\n",m*i-M[t]);flag=true;break;}
一定要注意中间乘起来的时候加上*1ll!!!
拓展BSGS
咕咕
斐波那契数列循环节
咕咕
二次剩余
PART2 组合数学部分
求组合数的几种方法
- 公式法 (这个复杂度很劣)
- 阶乘逆元求法 适用于多次查询,复杂度预处理O( n+logn ),查询接近O( 1 ),但是模数必须是质数。(100007不是质数)
(就是先O(n)预处理阶乘,然后算出来最大数的逆元,然后倒推回来。) - 杨辉三角递推求法 适用于多次密集小范围查询,复杂度预处理O( n^2 ),查询O( 1 )
- 费马小定理/exgcd求逆元 单次O( logn ),是最简单的方法,模数必须为质数
- 阶乘分解 适用于模数不为质数的求法。复杂度预处理O( nlogn ),查询O( 1 )
- Lucas定理(适用于处理long long级别大整数,但是模数不是很大(一般都是1e5级别)的情况)
lucas定理
\(lucas(n,m,p)=c(n\%p,m\%p)\times lucas(n/p,m/p,p)\),其中p是模数。
\(O(p)\)预处理之后,一次计算时间复杂度上界\(O(lognlogp)\)。
排列组合
这个蒟蒻我原先有过整理了,算是写了很多吧。戳我
不过那个是在NOIP前搞的了,所以现在看来又显得简单了一些。
所以现在特地来补充一下。
卡特兰数
以下内容摘抄自:这里
卡特兰数的公式
通项公式1:\(C_n=\frac{1}{n+1}C_{2n}^n=C_{2n}^n-C_{2n}^{n-1}\)
通项公式2:\(C_n=\frac{1}{n+1}\sum_{i=0}^n(C_n^i)^2\)
递推公式1:\(C_{n+1}=\frac{2(2n+1)}{n+2}C_n,\)且\(C_0=1\)
递推公式2:\(C_{n+1}=\sum_{i=0}^{n}C_iC_{n-i-1},\)且\(C_0\)=1
卡特兰数的应用
-
进出栈问题
对于一个足够大的进栈顺序为1,2,3...,n时有多少个不同的出栈序列? -
二叉树构成问题
有n个节点,问总共能构成多少种不同的二叉树。
我们可以假设,如果采用中序遍历的话,根节点第K个被访问到,则根节点的左子树有K-1个点,根节点的右子树有N-K个点,K的取值范围为1到N。 -
凸多边形的三角划分
一个凸的N边形,用直线连接他的两个顶点使之分成多个三角形,每条直线不能相交,问一共有多少种划分方案。
选择一个基边,显然这是多边形划分完之后某个三角形的一条边。图中我们假设基边是p1pn,我们就可以用p1、pn和另外一个点假设为pi做一个三角形,并将多边形分成三部分,除了中间的三角形之外,一边是i边形,另一边是n-i+1边形。i的取值范围是2到n-1。所以本题的解\(c(n)=c(2)*c(n-1)+c(3)*c(n-2)+...c(n-1)*c(2)\)。令\(t(i)=c(i+2)\)。则\(t(i)=t(0)*t(i-1)+t(1)*t(i-2)...+t(i-1)*t(0)\)。 -
在n*n的格子中,只在下三角行走,每次横或竖走一格,有多少中走法?其实向右走相当于进栈,向左走相当于出栈,本质就是n个数出栈次序的问题。
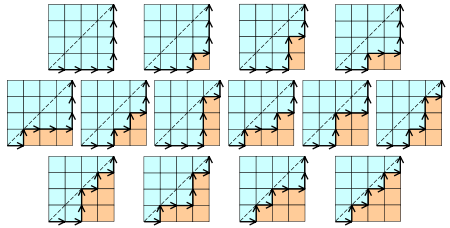
- 有n+1个叶子的满二叉树的个数?事实上,向左记为+1,向右记为−1,按照向左优先的原则,从根节点开始遍历.例如第一个图记为+1,+1,+1,−1,−1,−1,于是由卡特兰数的含义可得满二叉树的个数为Cn。

-
由n对括号组成的合法括号表达式的种类数为\(C_n\)
-
n+1个数连乘,不同的乘法顺序为\(C_n\)种。
-
在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?和凸包切割一个原理。
卡特兰数的前几项:1,2,5,14,42......
容斥
新开了一个,详情请看这个吧
PART3 线性代数部分
向量
n维向量可以看成n个数组成的n元组(或者说n个元素的数组)
几何意义:表示n维空间中的方向和长度
矩阵
行列式
一般用\(|A|\)或者\(det(A)\)表示A的行列式。
把一个n阶行列式中的元素\(a_{ij}\)所在的第i行和第j列划去后,留下来的n-1阶行列式叫做元素\(a_{ij}\)的余子式,记作\(M_{ij}\)。记\(A_{ij}=(-1)^{i+j}M_{ij}\),叫做元素\(a_{ij}\)的代数余子式。
一个n×n矩阵的行列式等于其任意行(或列)的元素与对应的代数余子式乘积之和,即
以下内容参考了这篇来自candy? dalao博客
行列式的性质:
- \(det(A)=det(A^T)\)
行列式的行和列是平等的,行满足那么列也满足。 - 令A为n×n矩阵。
- 若A有一行或一列包含的元素全为零,则det(A)=0。
- 若A有两行或两列相等,则det(A)=0。(因为两行互换,行列式变号)
- 一行乘上k,行列式乘上k
推论:行列式两行成比例或一行全0,值为0 - 两个行列式只有一行不同,他们的行列式和等于不同的行相加后的行列式
- 每行每列和均为0的矩阵行列式为0。
求法:用高斯消元的方法将其化成一个上三角矩阵,然后主对角线相乘就是行列式的值。
主子式
n−1阶主子式,就是对于r,第r行、第r列同时去掉后得到的新行列式
高斯消元
解线性方程组,在概率与期望的题中作为一种解题方法还是蛮常见的。
无解情况:化简后的有效方程组出现(0=d)型式不兼容方程,则无解 。(如下例)
无穷多解情况:化简后的有效方程组个数,小于未知数个数。这样的方程组有无穷多个解。(如下例)
矩阵树定理
用来解决生成树计数问题:对于一张包含N个节点的无向图,求包含N-1条边且这些边集能够构成一棵树的种类数。
定理:G的所有不同的生成树的个数等于其基尔霍夫矩阵C[G](度数矩阵-邻接矩阵)任何一个n−1阶主子式的行列式的绝对值。
证明:请看wzs dalao的博客 戳我
模板题:[HEOI2015]小Z的房间
计算几何
这个开成专题了,详情请参考同系列学习笔记->OI计算几何 简单学习笔记
PART4 我也不知道这是什么分类了
范德蒙矩阵
相关的主要就是求行列式。这个感觉百度百科上说的很详细了,也有证明,链接戳我。
点值表示
我们可以用n个不同的\(y_i=A(x_i)\),用这n个点来表示一个次数界为n的多项式,称作多项式的点值表示。
利用点值进行多项式加法和乘法只需要把\(y_i\)的值乘或加起来即可,时间复杂度\(O(n)\)
我们想到可以把系数表示转化成点值表示(求值),做乘法再转化回来(插值),就能快速计算卷积。
点值对应唯一的多项式,证明是可以将它转化成矩阵来推,与范德蒙矩阵有关,具体证明可以看《算法导论》。
拉格朗日插值公式
欧拉公式:\(e^{ix}=cosx+isinx\)
第一类斯特林数
用n个数组成k个圆排列的方案数
第二类斯特林数
dp[n][m]表示n个有区别的小球,放进m个相同的盒子里,且每个盒子非空的方案数
数论分块
求\(\sum i\times \lfloor \frac{k}{i}\rfloor\)
for(long long l=1,r;l<=n;l=r+1)
{
if(k/l!=0) r=min(n,k/(k/l));
else r=n;
ans+=(l+r)*(r-l+1)/2*(k/l);
}
莫比乌斯反演
其实是一种容斥。。。。
推荐pengym dalao的博客 戳我
二项式反演
其实是利用的容斥定理。以下是两种常见形式。
杜教筛
套路式:
现在要求的式子为\(\sum_{i=1}^nf(i)\)
那么我们找到合适的\(h,g\),使得\(h=g*f\)
那么根据狄利克雷卷积,我们有\(h(n)=\sum_{d|n}^{} g(d)f(\frac{n}{d})\)
\(\sum_{i=1}^nh(i)=\sum_{i=1}^n\sum_{d|i}g(d)f(\frac{n}{d})\)
我们令\(s(n)=\sum_{i=1}^nf(i)\),之后就可以进行推导了:
\(\sum_{i=1}^nh(i)=\sum_{i=1}^n\sum_{d|i}g(d)f(\frac{n}{d})\)
\(\sum_{i=1}^nh(i)=\sum_{d=1}^ng(d)\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}f(i)\)(这一步不理解的话可以自己找个例子试一试帮助理解)
\(\sum_{i=1}^nh(i)=\sum_{d=1}^ng(d)s(\lfloor\frac{n}{d}\rfloor)\)
\(\sum_{i=1}^nh(i)=g(1)s(n)+\sum_{d=2}^ng(d)s(\lfloor\frac{n}{d}\rfloor)\)
\(g(1)s(n)=\sum_{i=1}^nh(i)-\sum_{d=2}^ng(d)s(\lfloor\frac{n}{d}\rfloor)\)
当h(i)的前缀和可以很快地求出来之后(比如说时间复杂度O(1)),当我们对后面的式子进行整除分块时,求S(n)的复杂度为\(O(n^{\frac{2}{3}})\)
更详细的请见pengym dalao的博客 戳我
补:yyb dalao还有几篇复习向的有关多项式的博客,写的挺好的orz
PART5 博弈论
Nim游戏
结论:将每堆石子的石子个数异或起来,如果得到的结果为0,先手必败,否则先手必胜。
证明:对于一个异或和为0的局面,由于我们进行一次操作必然会改变局面的异或和,必然不能到达异或和为0的局面。对于一个异或和不为0的局面,设现在的异或和为s,考虑异或和s二进制下最高位j,我们找到一堆石子ai,满足ai二进制下该位为1(因为异或和的性质,该堆石子必然存在),那么\(ai\) \(xor\) \(s<ai\),也就是说必然存在到达异或和为0的局面的操作。
于是我们发现异或和是否大于0与先手是否必胜等价。
游戏的和
若局面X由若干个子游戏X1,X2,...,Xn构成,则\(SG(x)=SG(X_1) xo rSG(X_2)xor...xorSG(X_n)\)
SG函数
若干个平等博弈游戏之和定义为两人轮流操作,每次操作选择一个游戏进行一次操作,不能操作者为负的平等博弈。
对于非负整数组成的集合S,我们定义mex(s)为最小的没有在s中出现的非负整数。
对于局面x,我们定义mex(s)为最小的没有在s中出现的非负整数。
显然,若SG(x)>0,先手必胜,若SG(x)=0,先手必败。
SG定理:平等博弈游戏和的SG函数等于各游戏SG函数的异或和。
证明:
我们只需要证明对于一个可拆分成若干个子游戏的平等博弈,若其子游戏SH异或和为x,其不能通过一次操作到达异或和为x的状态且能到达异或和为0~x-1内的每个状态。
首先,对于一个子游戏进行操作,必然会改变其SG函数的值,异或和也必然会改变,故不能到达异或和为x的状态。
之后再证能到达异或和为0~x-1内的每个状态,证明与Nim游戏异曲同工。
反Nim游戏
规定取走最后一块石子的人输(也就是轮到一个人不能操作的时候他赢)
结论:若每对石子都只有一个石头,石子数异或和为0时先手必胜,否则石子数异或和非0时先手必胜,其他情况先手必败。
证明:
如果每堆石子都只有一个石头,因为奇偶性,结论显然。
如果只有一堆大于1的石头(此时异或和一定非0),我们必然能将其变成1或者0而转到必败态。所以先手必胜。
若不止一堆,那么操作后至少会剩一堆。那么进行几轮之后,就相当于进入了上一种局面,所以是先手必败。
例题 [SHOI2008]小约翰的游戏john
反博弈
改变了一点,就是将不可操作定义为胜利。
结论:如果任意子游戏x都满足当SG(x)=0时,x不可操作或者x一定能转移到SG函数为1的状态,那么当以下两个条件同时满足或者同时不满足的时候,先手必胜。
1、所有子游戏的SG函数值异或和为0
2、所有子游戏的SG函数值小于等于1
PART6 概率与期望
全概率公式
把样本空间S分为若干个不相交的部分B1,B2,B3....,Bn,则\(P(A)=P(A|B_1)\times P(B_1)+P(A|B_2)\times P(B_2)+...+P(A|B_n)\times P(B_n)\)。
数学期望
随机变量X的数学期望EX就是所有可能值按照概率加权的和,在非正式场合中,数学期望可以被称作“在平均情况下”。
在解决数学期望相关的题目时,可以先考虑直接使用数学期望的定义求解,计算出所有可能取值,以及对应的概率,最后加权求和。以下还有两个比较常用的性质——
期望的线性性
有限个随机变量之和的数学期望等于每个随机变量的数学期望之和。
全期望公式
类似于全概率公式,把所有情况不重复、不遗漏地分成若干类,每类计算数学期望,然后把这些数学期望按照每类的概率加权求和。
PART7 群论
置换
(注:以下部分内容参考自蓝书)
置换是把n个元素做一个全排列。比如说一般把1变成\(a1\),2变成\(a2\)...的置换记作:
置换可以定义乘法,对应于函数复合。有封闭性。满足结合律,但是不满足交换律。有单位元。有逆元。
为了处理方便,常常把置换分解成循环的乘积。而且对于任意置换,只有唯一的方法表示成不相交的循环的乘积比如说
为什么任意置换都可以这样分解?因为我们把每个元素看程一个节点,如果a变成b,连一条有向边\(a\to b\),则每个元素恰好有一个后继节点和一个前驱节点。(就是每个点的入度和出度都为1),那么这样的图只能是若干个有向环,其中每一个环都对应一个循环。
Burnside引理
对于一个置换f,若一个着色方案s经过置换后不变,那么称s为f的不动点。将f的不动点数目记为\(C(f)\),则可以证明等价类数目为所有的\(C(f)\)的平均值。(注意不动也是一种方案)
polya定理
(以下内容摘自beisong dalao的博客)
polay定理实际上是burnside引理的具体化,提供了计算不动点的具体方法。
假设一个置换有k个循环,易知每个循环对应的所有位置颜色需一致,而任意两个循环之间选什么颜色互不影响。因此,如果有m种可选颜色,则该置换对应的不动点个数为\(m^k\)。用其替换burnside引理中的C(f),得到等价类数目为:
其中|F|表示置换的数目,ki表示第i个置换包含的循环个数。



