OI树上问题简单学习笔记

最小生成树

切割性质假定所有边权均不相同。设S为既非空集也非全集的V的子集，边e是满足一个端点在S内，另一个端点不再S内的所有边中权值权值最小的一个，则图G的所有生成树均包含e。
回路性质。假定所有边权均不相同。设C为图G的任意回路，边e是C上权值最大的边，则图G的所有生成树均不包含e。

增量最小生成树

从包含的n个点的空图开始，依次加入m条带权边。每加入一条边，输出当前图中最小生成树权值（如果当前图不联通，输出无解）。
如果加入一条边（u,v）后，图中恰好包含一个环，根据回路性质，删除该葫芦上权值最大的边即可，因此只需要在加边之前的MST中找到u到v唯一路径上权值最大的边，再和e比较，删除权值较大的一条。由于路径唯一，可以用DFS或者BFS找到这条u到v的路径，总时间复杂度为\(O(nm)\)。

最小瓶颈生成树

给出加权无向图，求一个最小生成树，使得最大边权值尽量小。
每颗最小生成树一定是最小瓶颈生成树，每颗最小瓶颈生成树却不一定是最小生成树

最小瓶颈路

给定加权无向图的两个结点u和v，求出从u到v的一条路径，使得路径上的最长边尽量短。
我们直接求出这个图的最小生成树，则起点和终点在书上的唯一路径就是我们要找的路径，这条路经上的最长边就是问题的答案。

每对结点间的最小瓶颈路

给出加权无向图，求每两个结点u和v之间的最小瓶颈路的最大边长\(f(u,v)\)
我们先求出来最小生成树，同时计算\(f(u,v)\)，每访问一个结点u时，考虑所有已经访问过的老结点x，更新\(f(x,u)=max(f(x,v),w(u,v))\)，其中v是u的父亲结点。（使用dfs实现上述过程）

次小生成树

戳我

树的重心

树上一点，满足删除该点时，树内剩下的子树最大节点数最小。

性质

1、树的重心每棵子树的大小一定小于等于\(n/2\)

2、每颗子树的大小都小于等于\(n/2\)的点一定是这棵树的重心（就是上一个的逆定理）

3、树中所有点到某个点的距离和中，到重心的距离和最小（如果有两个重心，他们的距离一样）
证明：我们考虑使用调整法，设当前最优决策为u点，v为u的任意相邻节点。记size(x)为当u为整棵树的根时，以x为根的子树的节点的大小。
u为全局最优决策当且仅当\(n-size(v)\ge size(v)\),否则最优策略一定在不满足该条件的v的子树中。
我们化简这个式子，即\(size(v)\le n/2\)
由定理2得，该点为树的重心。

4、两棵树通过一条边相连成为一颗新的树，新树重心一定在原来两棵树得重心的路径上。（注意中心不止一个的情况）
例题：cf civilization

怎么找重心？

方法1：处理出每个节点的𝑠𝑖𝑧𝑒，依次枚举点，模拟删除该点后各子树大小，更新最优解。

方法2：采用“调整法”的思想，从一个点出发，调整过去。

两种方法都是Ο(𝑛)的。

树的直径

树（可带权）上最长的简单路径。
1、一棵树的直径可能有若干条，但是有一点显然——他们一定两两相交，不然我们就一定可以找出一条更长的。

2、所有直径的交集一定非空。因为如果三条直径两两相交。如果他们没有共同交集，那么就会形成环。然后我们可以一直推广到所有直径的情况。

3、以树上任意一个点作为起点的最长路径，重点一定是直径上的一个端点。
在此捞上栋栋小哥哥的证明：

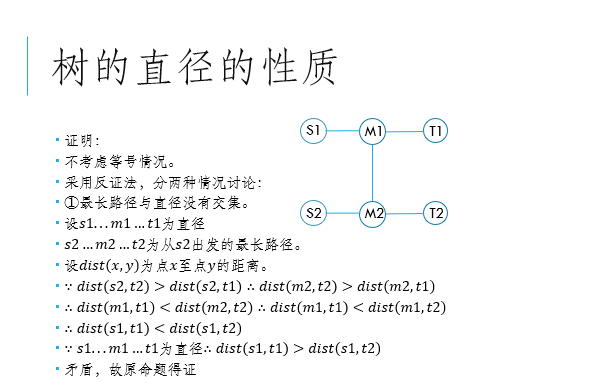
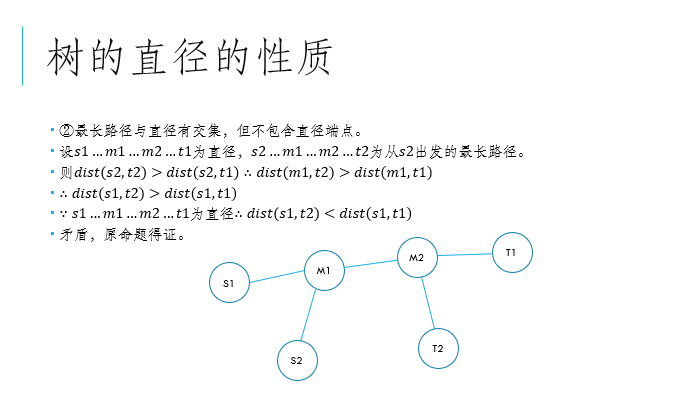
4、对于两条相交直径，他们不相交的部分一定对称。

5、两棵树用一条边合并，新树的直径两端一定是原本两棵树直径四个端点中的两个。
证明：（1）直径不经过新边这个时候显然是原本两条直径中的一条。否则就不满足直径的定义了。（2）直径经过新边。新边两端分属两棵树，那么这条直径的新边的两端部分肯定是从这两个点出发在各自树中的最长路径。根据性质3，端点还是四个端点的其中之二。

怎么找直径

由于性质3，我们可以通过两次bfs或者dfs来确定直径——任选一点，通过搜索找到从该点出发的最长路，由性质得到，终点为直径的一个端点。从该端点出发，再通过搜索找到最长路，由定理得，此终点一定是直径的另外一个端点。
代码这样写：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cmath>
#define MAXN 300010
using namespace std;
int n,m,k,t;
int head[MAXN<<1],done[MAXN],dis[MAXN];
struct Edge{int nxt,to,dis;}edge[MAXN<<1];
inline void add(int from,int to,int dis)
    {edge[++t].nxt=head[from],edge[t].to=to,edge[t].dis=dis,head[from]=t;}
inline void solve(int x)
{
    done[x]=1;
    for(int i=head[x];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(!done[v])
        {
            dis[v]=dis[x]+edge[i].dis;
            solve(v);
        }
    }
}
int main()
{
    #ifndef ONLINE_JUDGE
    freopen("ce.in","r",stdin);
    #endif
    scanf("%d%d",&n,&k);
    for(int i=1;i<n;i++)
    {
        int x,y,w;
        scanf("%d%d%d",&x,&y,&w);
        add(x,y,w),add(y,x,w);
    }
    solve(41);
    int maxx=-0x3f3f3f3f,pos;
    for(int i=1;i<=n;i++) 
        if(dis[i]>maxx)
            maxx=dis[i],pos=i;
    memset(dis,0,sizeof(dis));
    memset(done,0,sizeof(done));
    solve(pos);
    maxx=-0x3f3f3f3f,pos;
    for(int i=1;i<=n;i++)
        if(dis[i]>maxx)
            maxx=dis[i],pos=i;
    printf("%d\n",maxx);
    return 0;
}

但是要注意！这种方法对于有负权的树，求直径是错的！！

不过还有一种肯定是正确的算法——树形DP

inline void dp(int x)
{
    done[x]=1;
    for(int i=head[x];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(done[v]) continue;
        dp(v);
        ans=max(ans,d[x]+d[v]+edge[i].dis);
        d[x]=max(d[x],d[v]+edge[i].dis);
    }
}

遍历序列

欧拉序

从根节点开始dfs遍历树——在点x时，走到一个未遍历过的儿子,或者儿子已经全部遍历过从x返回到父亲时，以此法得到的遍历序列是欧拉序。

DFS序

从根节点开始dfs遍历树，一个节点第一次被遍历到时加入到序列中，以此法得到的遍历序列是dfs序。

括号序

从根节点开始dfs遍历树，一个节点第一次被遍历或者遍历完儿子要退出时将其加入到序列中，以此法得到的遍历序列是括号序。

应用

1、将树中子树表示为遍历序列的一段区间。（括号序）

2、判断一个点是否在以另外一个点为根的子树里。
（设一个点x在dfs序列中位置为dfn(x),那么如果点y在以x为根的子树离=>\(dfn(x)\le dfn(y)<dfn(x)+size(x)\)

3、和2等价的，还可以推出判断点x是否在点y到根节点的路径上（只要判断不在子树里就可以了）

4、再考虑这样的一类询问，求点x到根路径上所有点的权值和，且存在修改点权操作。
显然，每个点的权值，对以该点为根的子树的所有点都有贡献，所以每次修改操作（初始化时给点赋值也看成修改）就可以将以该点为根的子树所有点答案加上修改的值。
处理时我们可以开一颗全局线段树，每个点在其中的下标就是该点的dfs序，值为该点的权值。
求答案时就是单点查询该点在线段树中的权值，修改时就是对整棵子树进行区间修改。
但是还有更简单的方法！我们考虑括号序列。
我们开一个大小为2n的数组，点x在位置\(arr_x\)插入权值，从位置\(lea_x\)插入权值的相反数，做一次前缀和后，设\(sum_i\)为前i项的和，显然点x到根节点的路径权值就是\(sum_{arr_x}\)
维护这个可以修改的前缀和数组可以用树状数组qwq

树链剖分（轻重链剖分）

定义：

1.𝑠𝑖𝑧𝑒(𝑢)为节点𝑢为根的子树的节点大小。
2.令𝑣是𝑢的儿子中𝑠𝑖𝑧𝑒(𝑣)最大的儿子（如果有多个，则任选一个），则称边(𝑢,𝑣)为重边，𝑣为𝑢的重儿子。
3.重路径：一条路径为重路径，当且仅当这条路径全由重边组成。
4.轻边：令𝑤是𝑢的儿子(𝑤≠𝑢)，那么称边(𝑢,𝑤)为轻边（即使𝑠𝑖𝑧𝑒(𝑣)=𝑠𝑖𝑧𝑒(𝑤)），𝑤为𝑢的轻儿子。

算法步骤

第一步，dfs出每个点的size。
第二步，找出每个点的重边，给点重新编号（DFS序），并将重边连为重链。
第三步，建立一个以新编号为下标的数据结构（一般都是线段树吧），维护树上的信息。

啊。。。。其他的东西去参考专门的博文吧qwq，我这里又不是讲树链剖分的。~~我的初衷是整理给自己看的~~

时间复杂度

单点修改和查询\(O(log(n))\),路径修改和查询为\(O(log(n)^2)\)

性质

1、如果v是u的儿子，且\((u,v)\)是一条轻边，那么\(size(v)<\frac{size(u)}{2}\)

2、令𝑙𝑖𝑔ℎ𝑡𝑑𝑒𝑝𝑡ℎ(𝑢)表示从𝑢到根经过的轻边个数
则有\(𝑙𝑖𝑔ℎ𝑡𝑑𝑒𝑝𝑡ℎ(𝑢)≤𝑙𝑜𝑔_2^𝑛\)
由定理8，如果经过了一条轻边，当前子树点的个数至多变为原来的一半。最初子树的点为𝑛，𝑢的子树的点的个数至少为1，所以至多经过logn条轻边。
由这个引理，我们也可以得知，每个点到根的路径上的轻边和重路径条数都不超过logn。

dsu on tree

本质是树上启发式合并，可以解决多数无修改的子树查询问题。
例如：每个点有一个颜色，询问每个子树中颜色种类数。

做法

首先，对每个点求出重儿子和轻儿子，维护一个颜色为下标的桶，开始dfs，假设当前到点x我们先将x的轻儿子都递归，每次退出递归时把桶都清空。
最后在递归x的重儿子，返回时无需清空。然后再将除重儿子的部分加进来，即可得到x子树的桶。

时间复杂度？

考虑一个点暴力加入和暴力清空的次数，显然和它到轻边的数量有关，那么一个点只会有log次。

kruskal重构树

参考自niick dalao的博客传送门
类似kruskal算法，先将边权排序，然后对于两个不在一个并查集内的节点，我们新建节点，该点点权为这条边的边权，并把这两个点向它连。之后更新它们的父亲。
这棵树是以最后建立的节点为根的有根树，如果原图不连通，那么就遍历一遍，找到每个并查集的根作为这个森林中对应树的根。

性质（由开始对边的排序决定）

是一个大/小根堆
两个节点的lca的权值是原图中其之间路径上的最大边权的最小值（或者最小边权的最大值）

长链剖分

选择最深的子树进行剖分。
与重链剖分类似，对于树高最高的儿子子树，称为长儿子，多个仍选择一个，其余都是短儿子。

经典应用是求K级祖先和一些和树上的深度有关的题目；

博客参考：zzq dalao的博客戳我

点分治

咕咕咕qwq不想写总结了qwq

LCT

性质（摘自flashhu dalao）博客链接：戳我

每一个Splay维护的是一条从上到下按在原树中深度严格递增的路径，且中序遍历Splay得到的每个点的深度序列严格递增。
每个节点包含且仅包含于一个Splay中
边分为实边和虚边，实边包含在Splay中，而虚边总是由一棵Splay指向另一个节点（指向该Splay中中序遍历最靠前的点在原树中的父亲）。
因为性质2，当某点在原树中有多个儿子时，只能向其中一个儿子拉一条实链（只认一个儿子），而其它儿子是不能在这个Splay中的。
那么为了保持树的形状，我们要让到其它儿子的边变为虚边，由对应儿子所属的Splay的根节点的父亲指向该点，而从该点并不能直接访问该儿子（认父不认子）。

LCT解决动态DP

虚树

其实就是对树上的信息进行了简化的一种方法。对于一棵树，如果我们提前知道一些询问点，那么我们可以考虑只保留根节点，询问点，以及他们之间的LCA。
先贴两个感觉讲的不错的链接：1 2
例题：SDOI2011消耗战
 yyb神犇的题解

prufer序列

请看这个

我们定义叶子结点为度数为1的节点。

将无根树转换成prufer序列的方法：

每次寻找一个最小的叶子结点，把与它相连的点放入prufer序列里，然后从树上删掉这个点以及它相连的边。直到剩下两个点为止。

将prufer序列转换成无根树的做法：

弄一个序列A：{1,2,...,n}（全排列），然后我们每次在A中寻找编号最小且没有在prufer序列中出现的点，将它与prufer序列中的第一个点连边，然后将这两个点分别从A和prufer序列中删掉。最后A中会剩下两个点，将它们连边即可。

最小树形图（最小有向生成树）

给定一个有向带权图G和其中一个节点u，找出一个以u为根节点，权和最小的有向生成树。这个生成树满足：

恰好有一个入度为0的点，称为根节点。
其他节点的入度均为1.
可以从根节点到达所有其他节点

算法：朱刘算法
就是先找出来前n-1条最小的彼岸，然后如果没有环就结束，有环就缩点继续重复上述过程。

inline bool solve(int n,int m,int root)
{
    ans=0;
    while(233)
    {
        int cnt=0;
        for(int i=1;i<=n;i++) id[i]=top[i]=fa[i]=0,minn[i]=INF;
        for(int i=1;i<=m;i++)
        {
            int u=edge[i].u,v=edge[i].v;
            if(u!=v&&edge[i].dis<minn[v])
                fa[v]=u,minn[v]=edge[i].dis; 
        }
        minn[root]=0;
        for(int i=1;i<=n;i++)
        {
            if(minn[i]==INF) return false;
            ans+=minn[i];
            int u;
            for(u=i;u!=root&&top[u]!=i&&!id[u];u=fa[u]) top[u]=i;
            if(u!=root&&!id[u])
            {
                id[u]=++cnt;
                for(int v=fa[u];v!=u;v=fa[v]) id[v]=cnt;
            }
        }
        if(!cnt) return true;
        for(int i=1;i<=n;i++) 
            if(!id[i])
                id[i]=++cnt;
        for(int i=1;i<=m;i++)
        {
            int u=edge[i].u,v=edge[i].v;
            int last=minn[v];
            if((edge[i].u=id[u])!=(edge[i].v=id[v]))
                edge[i].dis-=last;
        }
        n=cnt,root=id[root];
    }
}

矩阵树定理：

外向树:边的方向为根->叶子
内向树:边的方向为叶子->根

上三角矩阵:只有主对角线及其上方的位置有值的行列式,主对角线以下部分都是0;
行列式的求值:用高斯消元把这个行列式小成一个上三角矩阵的形式,然后直接把对角线上面的数乘起来就是这个行列式的值.
余子式:一个行列式的余子式就是这个行列式去掉一行一列后剩下的那个少了一维的行列式.

基尔霍夫矩阵:度数矩阵-邻接矩阵

无向图的生成树计数:该图的基尔霍夫矩阵的任意一个余子式的行列式的值.
有向图的外向树计数:基尔霍夫矩阵换成入度矩阵-邻接矩阵
有向图的内向树计数:基尔霍夫矩阵换成出度矩阵-邻接矩阵
有向图中的计数,余子式去掉的行列不能任意了,应该的根节点对应的那一行一列
注意如果有重边的时候,邻接矩阵可是记录的是两个点之间边的条数,而不是0/1(其实这是变元矩阵树定理)

变元矩阵树定理:对于有重边+边的权值有可能不为1的,我们把邻接矩阵换成边权值之和,然后按照上面的方法求出来的是是所有矩阵树的边权积之和.(所以说如果计算有重边的,我们可以直接设边为1,然后来达到计数的目的)

风浔凌

黑夜一无所有，为何给我安慰 博客搬迁到CSDN啦~~

OI树上问题 简单学习笔记