逆序数:
进行冒泡排序,统计期间交换次数
import copy e =[[1,3,1], [2,1,0], [2,0,1]] #求逆序数/冒泡法 def inverse_number(e): a=copy.deepcopy(e) c = [0,0,0] for n in range(len(a)): for i in range(len(a[n])): for j in range(3 - i): if j == 0: continue elif a[n][j] < a[n][j - 1]: k = a[n][j] a[n][j] = a[n][j - 1] a[n][j - 1] = k c[n]+=1 return c
行列式计算:

#求余子式 def yuzishi( e ): k=[0 for i in range(len(e))] for i in range(len(e)): b = copy.deepcopy(e) for m in range(len(b)): for n in range(len(b)): if n == i: b[m].pop(n) b.pop(0) k[i]=b return k ##求行列式/递归 def get_A( a ): sum=0 if len(a)==2: return a[0][0]*a[1][1]-a[1][0]*a[0][1] else: ge=yuzishi(a) for s in range(len(ge)): sum+=(-1)**s * get_A(ge[s])*a[0][s] return sum
矩阵求逆:
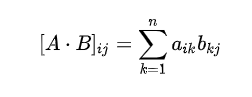
#伴随矩阵 def accompany(e): #定义返回数组 k = [[ 0 for j in range(len(e))] for i in range(len(e))] #求余子式 for m1 in range(len(e)): for m2 in range(len(e)): b = copy.deepcopy(e) for m3 in range(len(b)): for m4 in range(len(b)): if m4==m2: b[m3].pop(m4) b.pop(m1) answer=get_A(b) k[m1][m2]=answer #代数余子式 for m1 in range(len(e)): for m2 in range(len(e)): if (m1+m2)%2!=0: k[m1][m2]= -k[m1][m2] #转置 for m1 in range(len(e)): for m2 in range(len(e)): if m1>m2: m=k[m1][m2] k[m1][m2]=k[m2][m1] k[m2][m1]=m return k #逆矩阵 def inverse(e): lAl=get_A(e) if lAl==0: return for m1 in range(len(e)): for m2 in range(len(e)): e[m1][m2]/=lAl return e



