双线性模型（四）（HolE、ComplEx、NAM）

目录

• HolE
  • 组合表示
    • Tensor Product
    • 拼接，投影，非线性
    • 非组合方法
  • Holographic Embedding
  • 实验
• ComplEx
  • 关系作为低秩正规矩阵的实部
    • 建模关系
  • 应用于二元多关系数据
  • 实验
    • 自建数据集
    • 通用数据集
    • 负采样的影响
• NAM
  • 模型
    • NAM overview
    • DNN
    • RMNN(Relation-modulated Neural Network)
  • 实验
    • 文本蕴含
    • 三元组分类
    • 常识推理
    • 知识迁移学习

本文简要介绍双线性模型 HolE、ComplEx、NAM。

HolE

【paper】 Holographic Embeddings of Knowledge Graphs
【简介】 本文是麻省理工的研究人员发表在 AAAI 2016 上的文章，提出了 HolE(Holographic Embedding)，是一个基于向量循环关联操作的组合向量空间模型。

组合表示

不同论文里对同一类方法的表述不同，这里说的组合表示就是指的双线性这一类模型。模型对于三元组打分函数的定义如下：

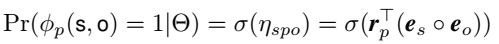
其中，\(\circ\) 代表组合操作，即对头尾实体根据它们的 embedding 创建一个组合向量。

常用的损失函数有两种：

一种是 logistic loss：

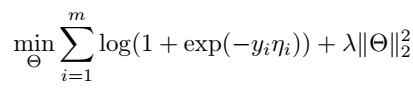
另一种是常见的 rank loss：

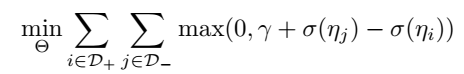
组合操作 \(\circ\) 具体可以有如下几种形式：

Tensor Product

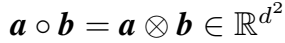
张量积，即 Hardamard 积：

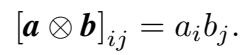
拼接，投影，非线性

\(\bigoplus\) 代表拼接操作，\(\psi\)代表非线性函数 \(tanh\)，投影就是指的线性变换。

非组合方法

指的非双线性的 Tran 系列模型：

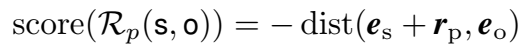
Holographic Embedding

本文提出的 HolE 定义的组合操作为循环关联（circular correlation）操作：

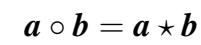
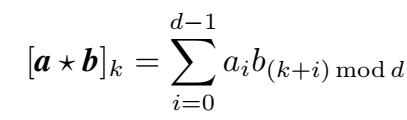
因此三元组的概率得分为：

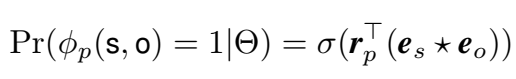
循环关联操作可以被视为张量积的压缩，这样可以在保证较少的计算量的前提下捕捉更多的交互，即保留更多的模型表现力。

HolE 与 RESCAL 的对比：

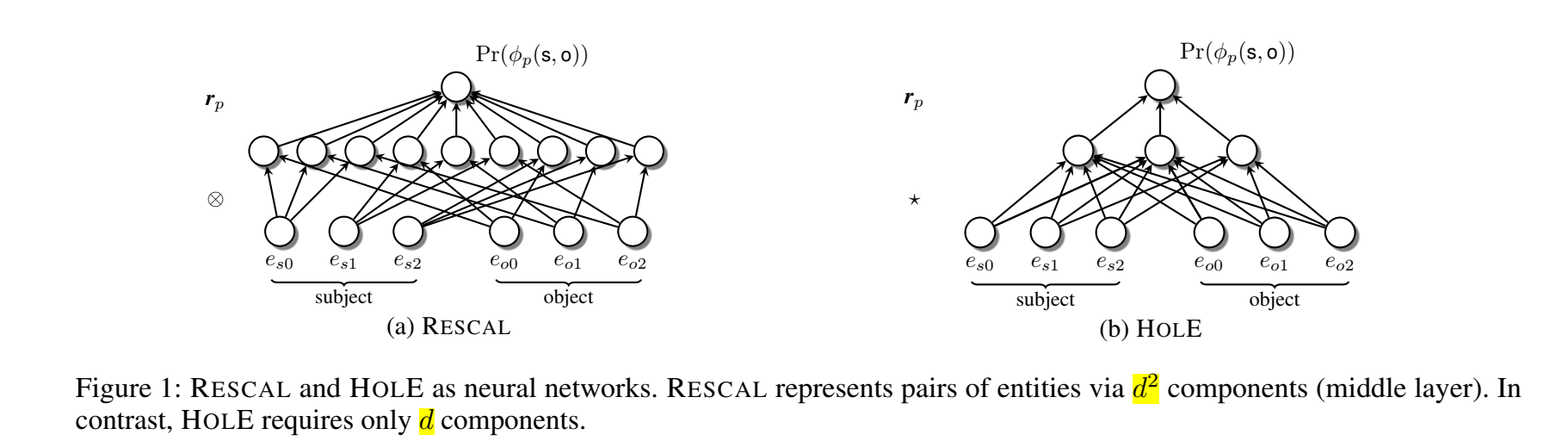
HolE 的时间复杂度关于维度 d 成拟线性（log线性），并可以通过快速傅里叶变换来计算：

这里用到了复共轭，SEEK 那篇文章提到 HolE 和 ComplEx是等价的。

循环关联操作的直观展示：

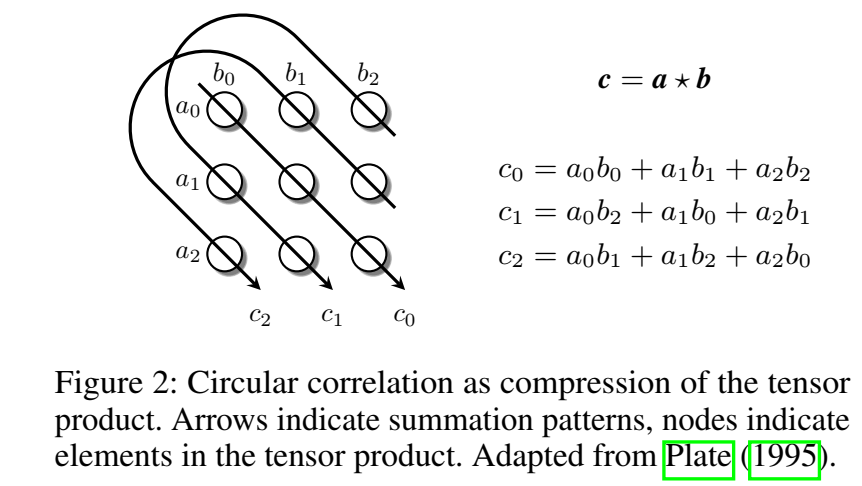
与循环卷积的区别：

循环卷积为：

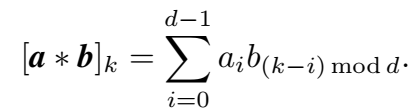
1. 卷积是对称的，满足交换律，而 correlation 不是，

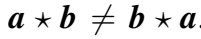
这样可以建模非对称关系。

2. 单个 component 的计算类似点积，

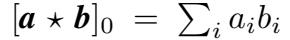
这种特性可以捕捉实体间的相似性。

实验

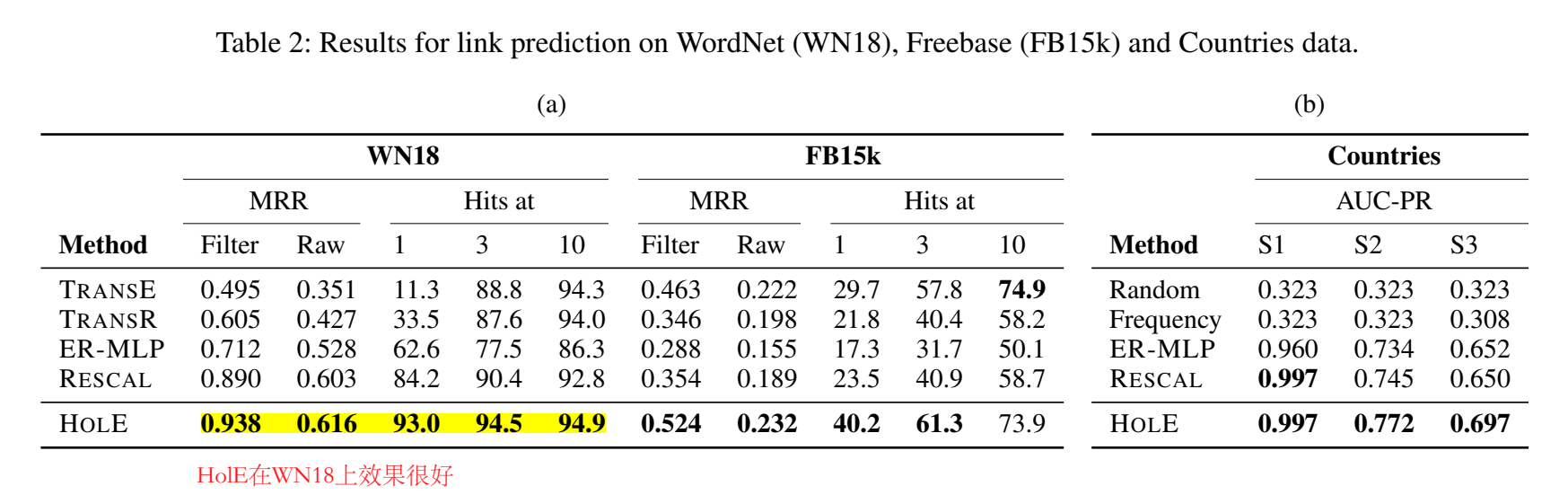
感觉 HolE 的效果比 TransE 提升了很多。

HolE 代码：https://github.com/mnick/holographic-embeddings

---

【小结】 本文提出了使用循环关联操作进行实体向量交互的全息 embedding 方法 HolE，可以在较少的计算量下捕捉到实体间尽可能多的交互。

ComplEx

【paper】 Complex Embeddings for Simple Link Prediction
【简介】 本文是法国和英国的研究学者发表在 ICML 2016 上的工作，提出了 ComplEx（Complex Embedding），主要思想是引入了复值向量，通过复值点积（Hermitian dot product）计算三元组得分，复值向量的实部是对称的，虚部是非对称的，取复值点积的实部作为三元组得分。

关系作为低秩正规矩阵的实部

正规矩阵（normal matrix）：与自己的共轭转置矩阵对应的复系数方块矩阵。

建模关系

对于某个关系，可以用一个邻接矩阵表示实体间是否存在这种关系：

对矩阵 \(X\) 做特征值分解：

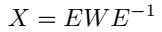
本文在复空间（complex space）进行特征值分解：

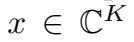
embedding \(x\) 由两部分组成：实向量成分 \(Re(x)\) 和 虚向量成分 \(Im(x)\)。

复向量的点积（Hermitian dot product）定义为：

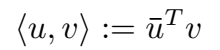
在复空间 X 矩阵（正规矩阵）的分解为：

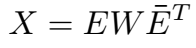
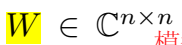
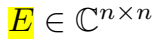
\(W\) 是特征值的对角矩阵，\(E\) 是特征向量的 unitary 矩阵。

X 取分解的实部：

一个实体的头实体表示是其尾实体表示的复共轭。

应用于二元多关系数据

三元组打分函数的计算：

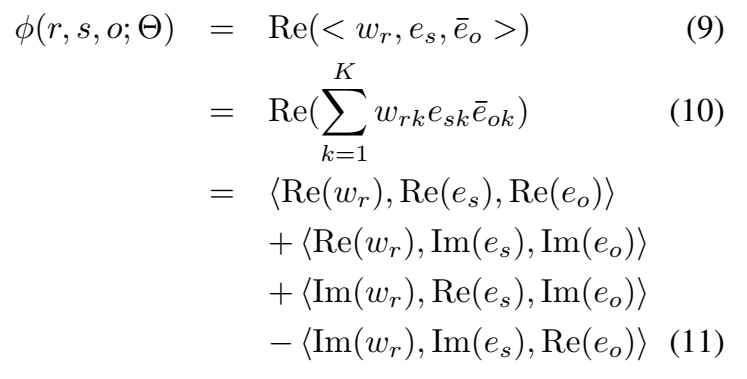
在复空间中，\(<e_o,e_s> = \overline{<e_s,e_o>}\)，因此实部 \(Re(<e_o,e_s>)\) 是对称的，而虚部 \(Re(<e_o,e_s>)\) 是非对称的，因此可以建模对称和非对称关系。

实验

自建数据集

构建了一个包含两个关系和 30 个实体的数据集，两个关系一个是对称的，另一个是非对称的。

采用 negative 的 log-likelihood 作为 loss：

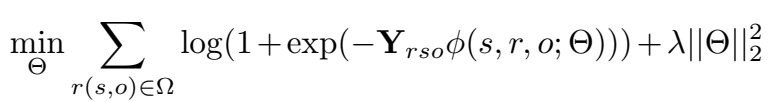
交叉验证的平均精度（cross-validated Average Precision, AUC）：

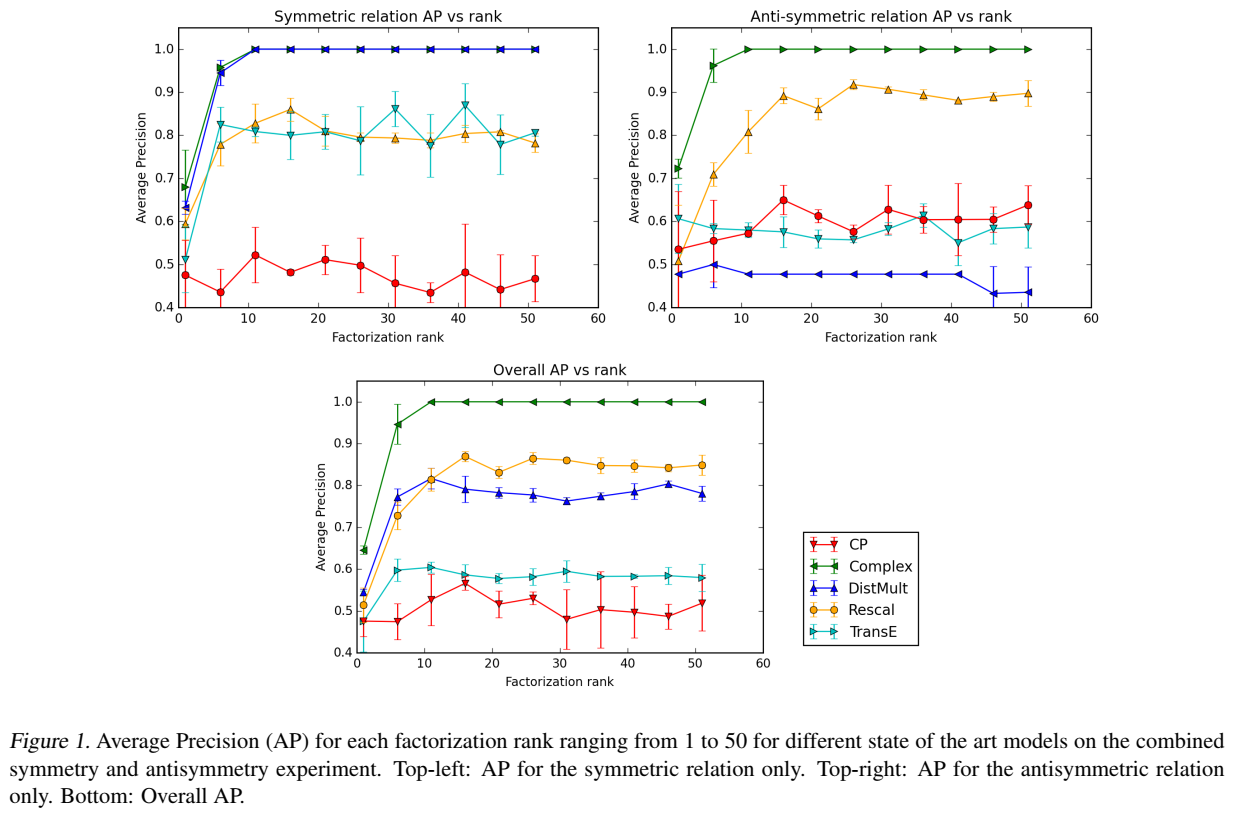
通用数据集

实验部分提到，进行了预实验，表明 log-likelihood 的效果比 ranking-loss 效果更好。

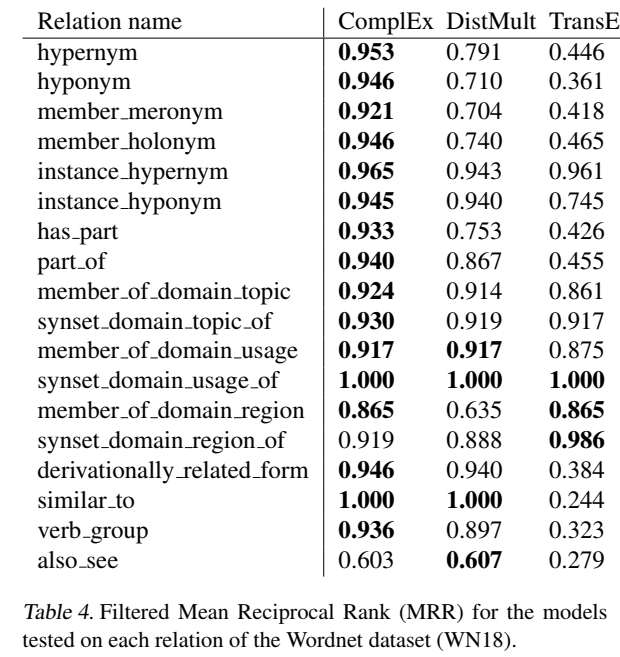
负采样的影响

ComplEx 代码：https://github.com/ttrouill/complex

---

【小结】 引入复值向量，在复空间进行矩阵分解，通过复值点积（Hermitian 点积）计算三元组得分。

NAM

【paper】 Probabilistic Reasoning via Deep Learning: Neural Association Models
【简介】 本文是中科大和科大讯飞联合发表在 IJCAI 2016 上的工作，本文提出了 NAM（Neural Association Model）用于概率推理，并具体化为 DNN（Deep Neural Network）和 RMNN（Relation Modulated Neural Network）两种形式。

模型

本文提出用神经网络建模两个 event 之间的关联：将一个 event 作为神经网络的输入，计算另一个 event 的条件概率。NAM 的 RMNN 形式可以进行高效的知识迁移学习。本文不属于双线性模型，应该归类为神经网络模型。

NAM overview

如果事件 \(E_2\) 是二值的（True or False），NAM 用 sigmoid 函数计算 \(Pr(E_2|E_1)\)；如果 \(E_2\) 是多值的，则 NAM 使用 softmax 计算 \(Pr(E_2|E_1)\)，输出多值向量。

可以表示为计算两个 event 关联概率形式的推理任务都可以套用 NAM 模型：

对于三元组分类任务，给定三元组 \((e_i,r_k,e_j)\)，\(E_1\) 由 头实体 \(e_i\) 和关系 \(r_k\) 组成，\(E_2\) 是一个二元事件，用于指示尾实体 \(e_j\) 是真或假。

NAM 的 loss 采用 log-likelihood 函数：

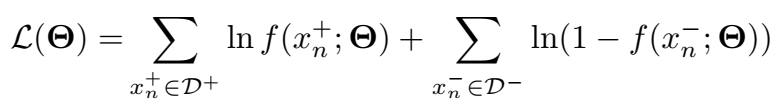
DNN

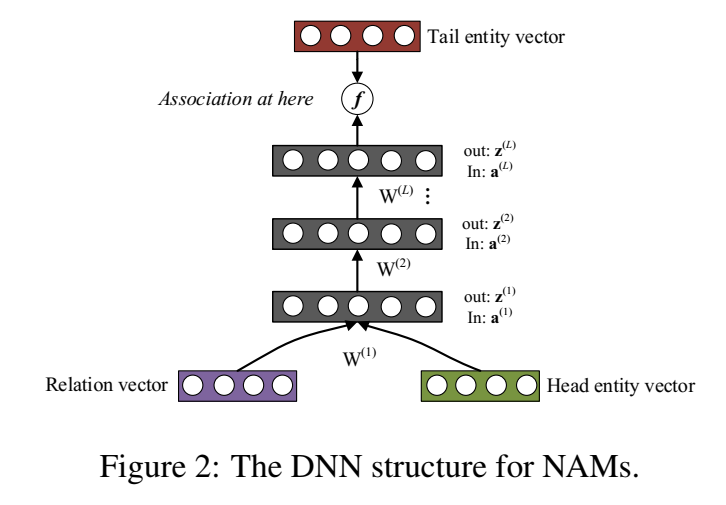
就是一个普通的前馈网络：

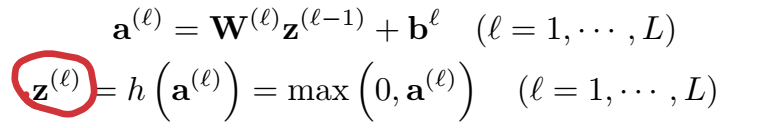
这里使用 sigmoid 函数输出三元组 \(x_n=(e_i,r_k,e_j)\) 成立的概率。

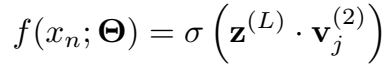
RMNN(Relation-modulated Neural Network)

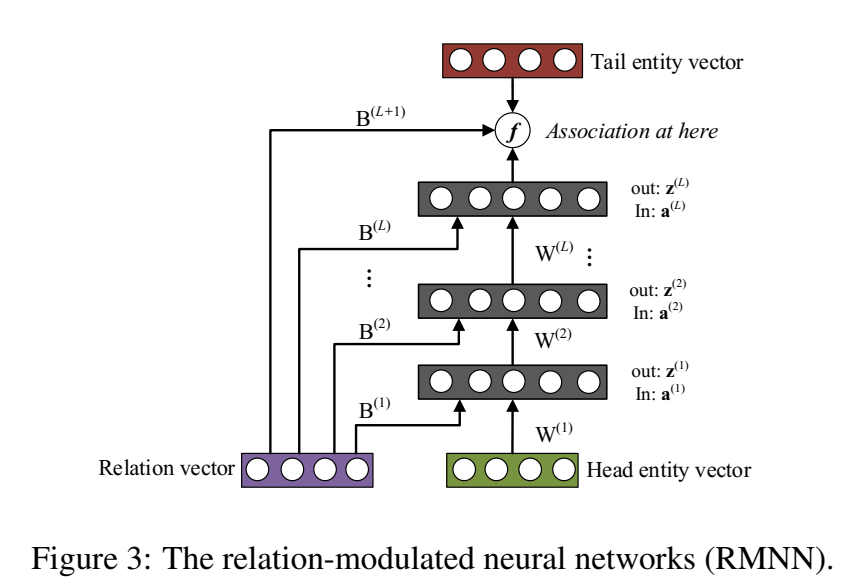
每一层使用上层的头实体经过变换后的输出和关系向量的原始表示作为输入：

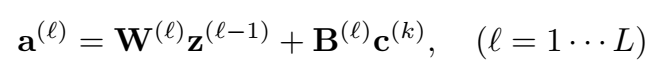
三元组最终得分：

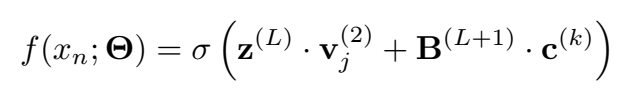
实验

文本蕴含

三元组分类

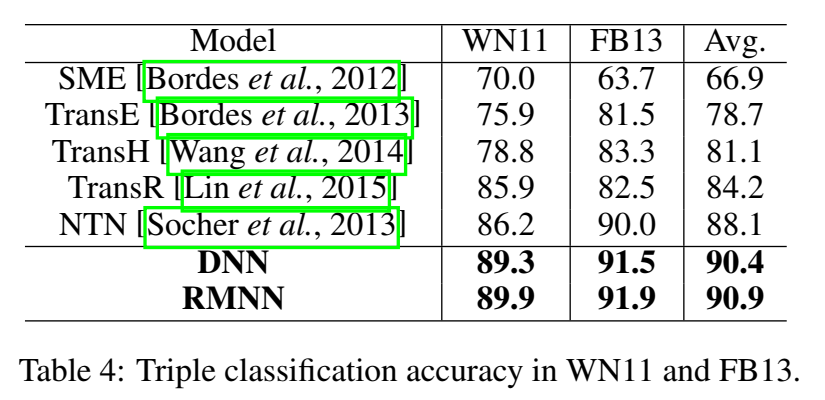
常识推理

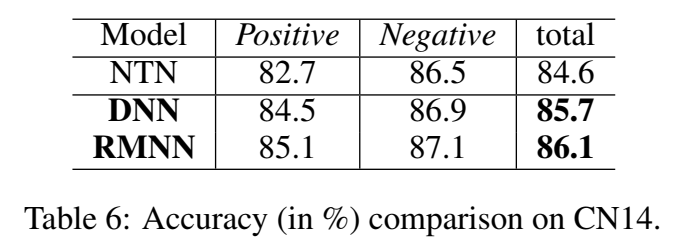
在 CN14 数据集上，RMNN 的效果都比 NTN 好一丢丢：

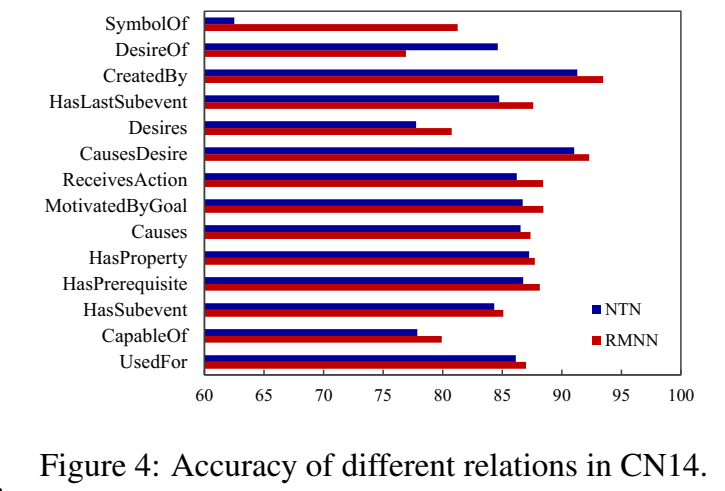
知识迁移学习

训练好 RMNN 后，如果想迁移到其他关系，只需要固定训练好的模型参数，为新关系学习新的 relation code（不知道是什么）即可。

如果不固定模型参数，在学习新关系时新旧关系的正确率变化如下，新关系的正确率上升，旧关系正确率稍有下降：

---

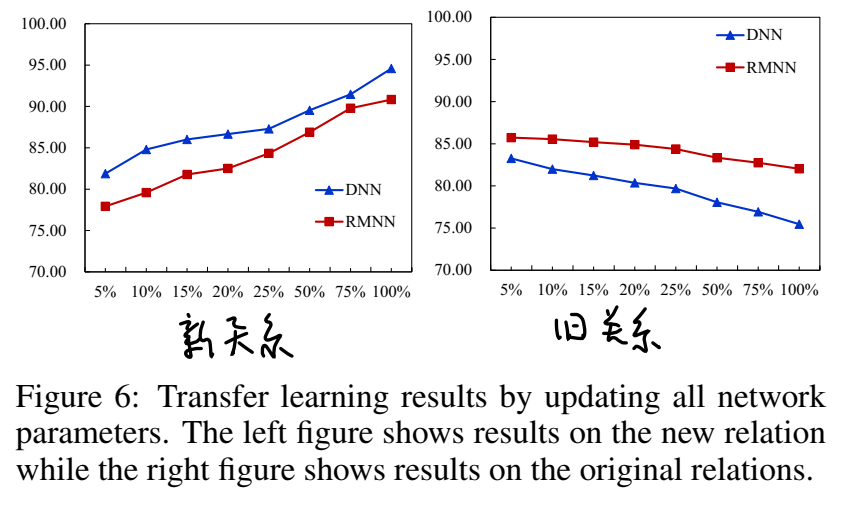
【总结】 本文提出用于概率推理（计算三元组得分）的神经网络框架 NAM，并具体化为 DNN 和 RMNN 两种形式。