翻译模型（六）（TransT、TorusE）

目录

• TransT
  • 论文
    • 问题提出
    • 方法概述
    • 先验部分
    • 似然部分
    • 目标函数
    • 实验
  • 代码
• TorusE
  • 论文
    • TransE 的缺点及 embedding 空间要求
    • Lie Group 和 Torus
    • TorusE
    • 实验
  • 代码

这篇博文记录 TransT 和 TorusE 的学习笔记。

TransT

paper: TransT: Type-Based Multiple Embedding Representations for Knowledge Graph Completion

论文

这篇文章之前我看过的，应该差不多是去年这会儿疫情在家的时候看的了吧。那时候看的时候还不太懂，这次看感觉能理解得清楚多了。打好基础果然是有用的，经过前面这些篇论文阅读的训练，每一篇论文都是能看懂了才过的，再拿到一篇新论文，即使稍有难度，也有自信去把它弄明白，弄明白后就有自信去看更复杂的文章。这是个循序渐进的过程，是个良性循环。从没有一蹴而就、由黑到白的事情，所有的“做到”都是量变的循序渐进。

这篇文章是上海交大的研究者发表在 ECML-PKDD 2017 (CCF-B类会议) 上的工作。文章提出了 TransT，T 代表 Type，用于挖掘知识图谱中的先验知识。TransT 提出使用条件概率代替联合概率对三元组进行评分，评分需要计算“似然”和“先验”两部分，“先验”部分使用基于类型的语义相似度度量，“似然”部分使用多成分向量解决。

问题提出

很多 KGE 模型忽略了知识图谱中包含的先验知识，在进行 KGC 时候，可以根据给定的 h 和 r 的类型信息，推测出 t 的类型信息，缩小对 t 进行预测时的筛选范围。并且在对三元组进行打分时，多数模型使用的是联合概率分布 p(h,r,t)，据论文所说，由于 h、r 已知，可能会影响对 t 的选择，因此使用条件概率 p(t|h,r) 表示三元组的得分更科学。

语义信息利用存在两个问题：实体表示和后验概率估计。实体表示涉及一词多义问题，使用多成分向量解决（和TransG一样）；后验概率估计利用贝叶斯公式，用似然函数和先验概率计算出来。其实多向量表示解决的就是后验概率中的似然函数部分。理论部分东西有点多，看起来有点乱，可能会梳理不清各部分的关系。

方法概述

对尾实体进行预测的后验概率为

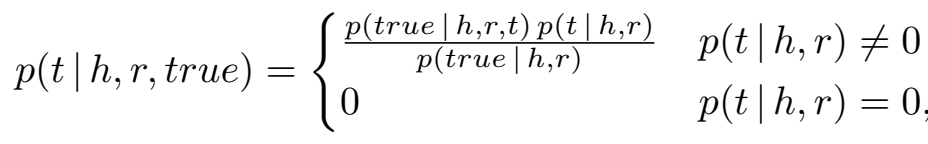
对于所有的候选尾实体，分母部分 \(p(true|h,r)\) 都是一样的，因此忽略不计，所以头尾实体和关系预测的后验概率正比于：

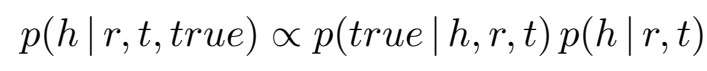
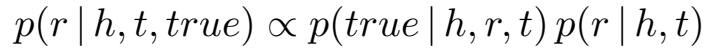
后验概率由似然 \(p(true|h,r,t)\) 和先验 \(p(t|h,r)\) 两部分组成，下面分别介绍两部分的计算方法。

先验部分

先验部分 \(p(t|h,r)\) 使用基于类型的语义相似度度量。

1. 基于类型的语义相似度

如上图中例子，同一关系下的头实体通常有相同的类型，尾实体也有相同的类型，将该关系的头实体共有的类型指定为该关系的 "head type"，同理也有 "tail type"。

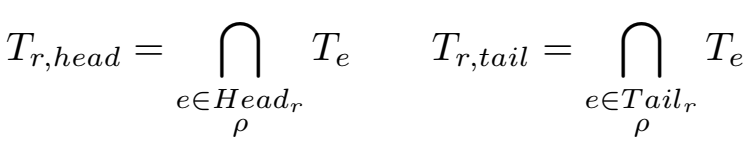
\(\rho\) 是控制严格取所有/大部分实体类型交集作为关系类型的参数。

使用 Jaccard 相似度利用实体/关系类型计算它们之间的语义相似度：

关系的头向语义和头实体的相似度：

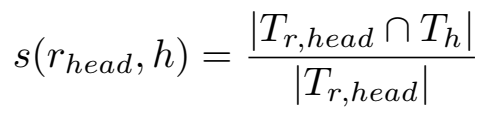
关系的头向语义和头实体的相似度：

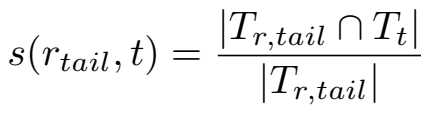
头尾实体的相似度：

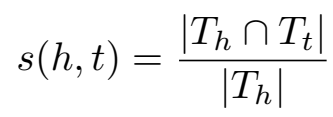
2. 先验概率估计

据此类型语义相似度计算先验概率：

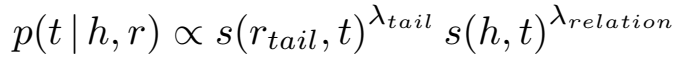
由于 h 和 r 对 t 的先验概率有不同的影响，因此引入了相似度权重 \(\lambda_{relation},\lambda_{head},\lambda_{tail} \in {0,1}\)。

同理有：

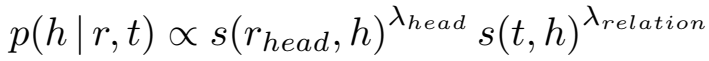
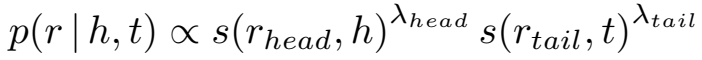
似然部分

文中说，实体包含的丰富语义难以被精确表示，由此造成了似然 \(p(true|h,r,t)\) 度量的难度。文章应用多 embedding 表示解决该问题。

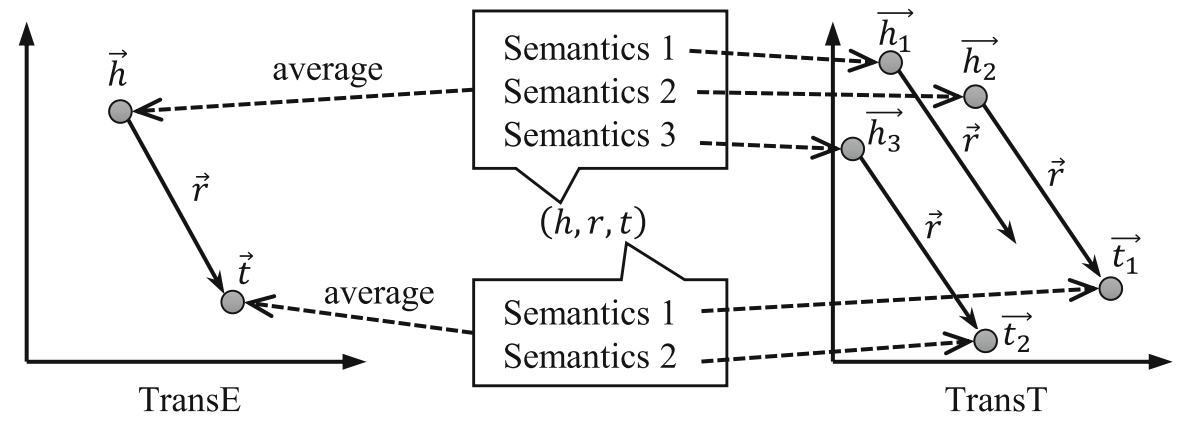
如图，每个实体有多个语义，关系有一个语义。似然 \(p(true|h,r,t)\) 被定义为头尾实体的各个语义成分向量的加权期望组合。

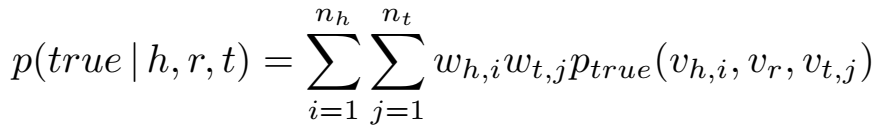
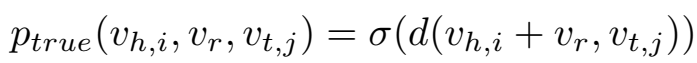
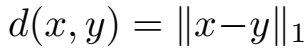
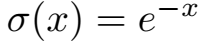
同 TransG 一样，实体所含语义成分的个数由 CRP（Chinese restaurant process，一个 Dirichlet 过程）确定。生成新的语义向量的概率为：

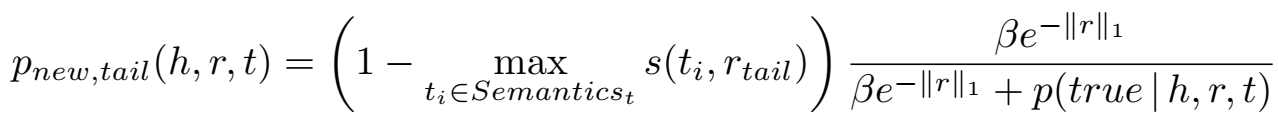
具体地，对于 t，在以下两种情况下更有可能生成新的语义成分：一是当现存的语义与 r 差异很大时（公式中括号部分），二是当现存的语义成分集不能准确地表示 t 时（公式中分数部分）。

目标函数

负采样：预测什么就替换掉什么。

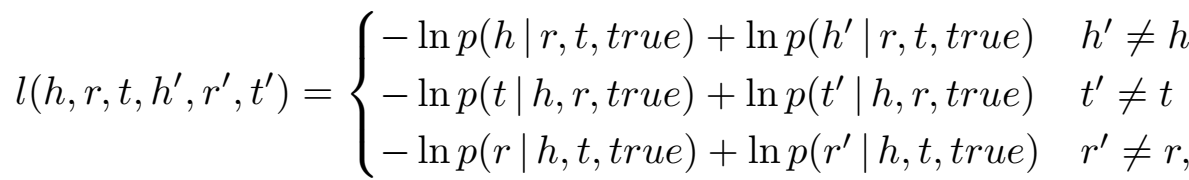
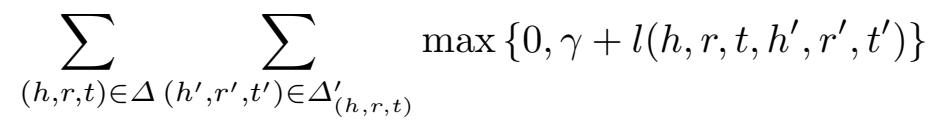
实验

实验包括：实体预测、关系预测、三元组分类、语义向量分析。数据集使用了 WN18 和 FB15k。除了几个 Trans 系列的模型，主要与几个使用外部信息的模型进行了对比。

1. 实体预测

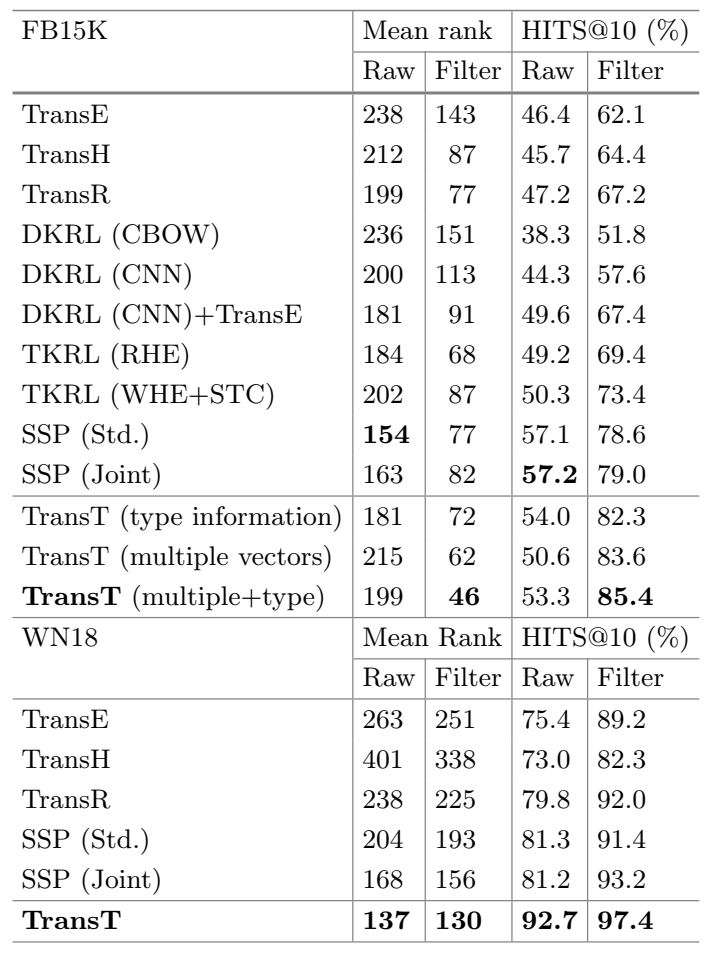
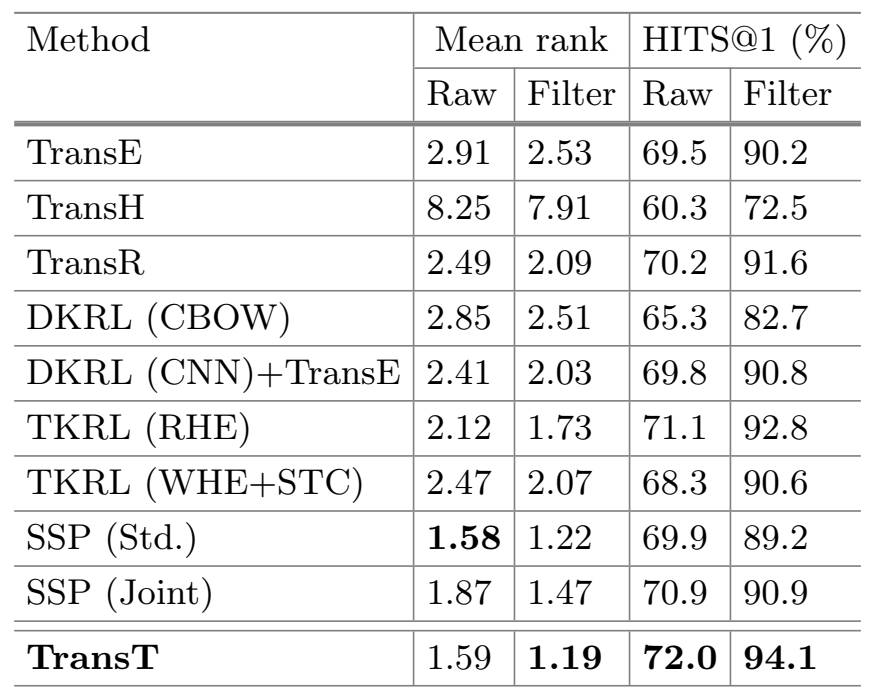
2. 关系预测（FB15k）

3. 三元组分类（FB15k）

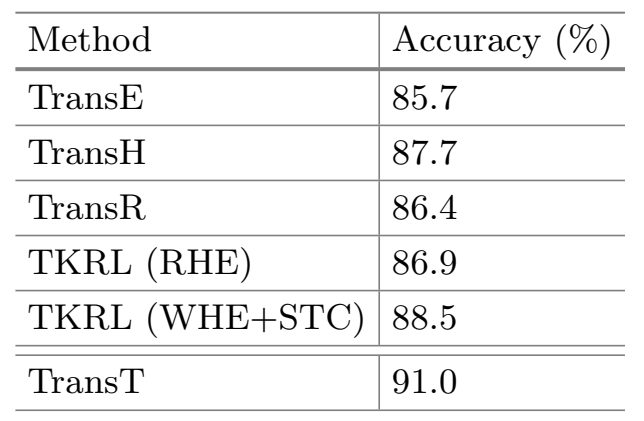
4. 语义向量分析（FB15k）

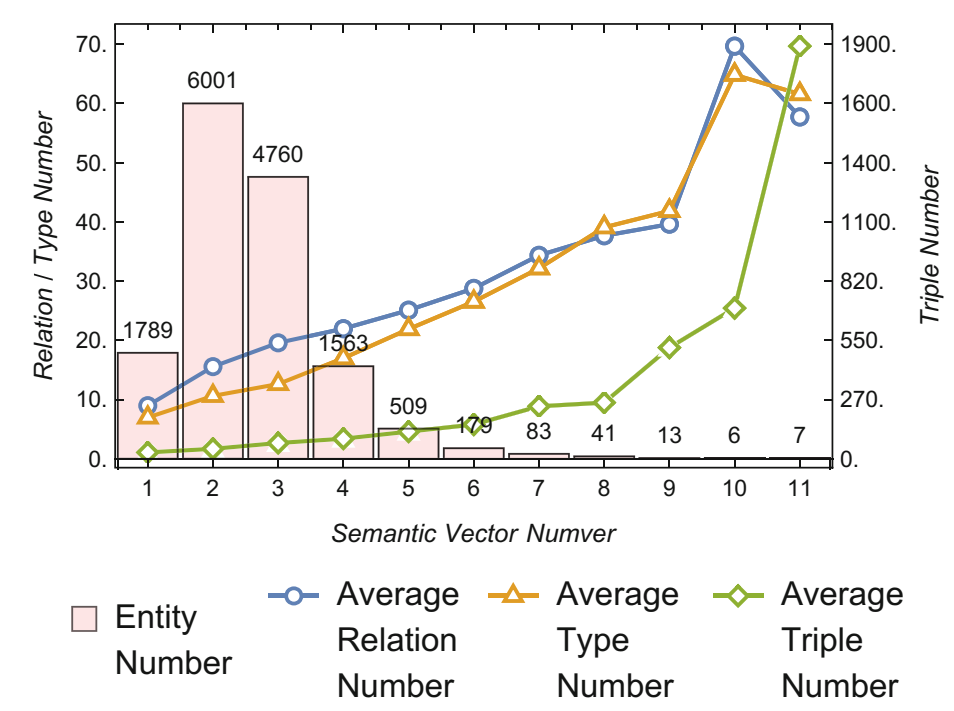
上图表明语义成分较多的实体拥有更多的关系数量、类型数量和三元组数量。

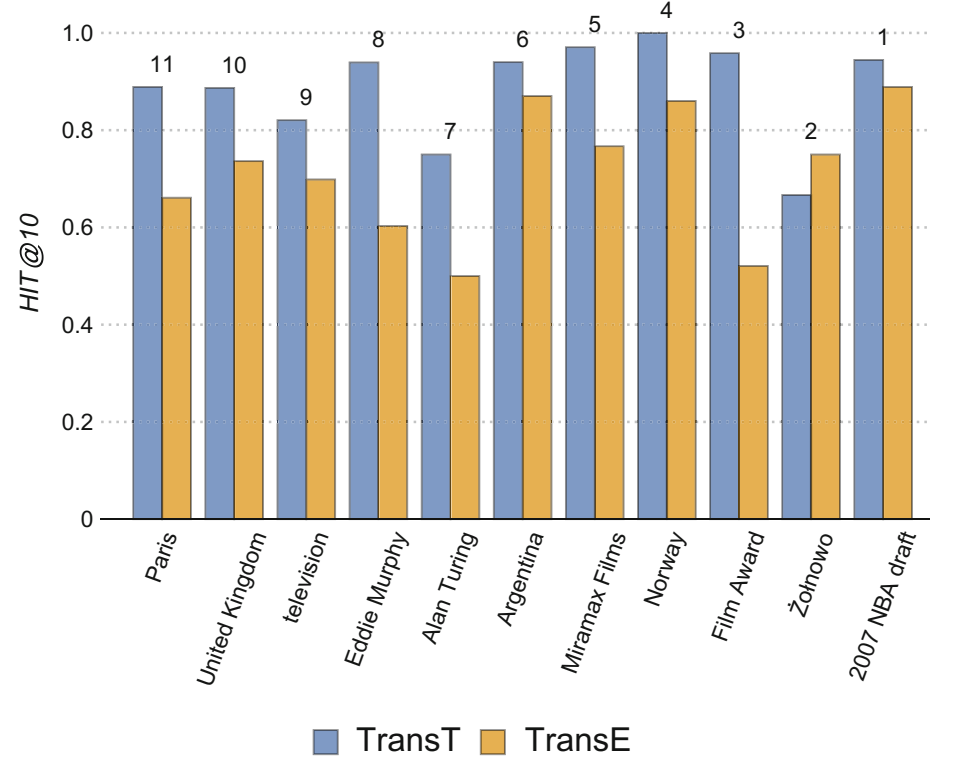
上图是某些实体包含的语义成分的数量及预测准确率，对于包含语义个数比较高的（如“Paris”、“Alan Turing”），TransE 的预测准确率很低，而 TransT 大幅度提升了对于这部分实体的预测效果。

代码

文章非常诚恳地给出了代码：https://github.com/shh/transt ，还是用 C++ 实现的，没有细看。

---

小结： 这篇文章的干货是真的多，比之前发表在顶会的 Trans 模型内容都要多，看了快两天才梳理个差不多。感觉这套方法论还是 make sense 的，能成体系，如果这就是一篇普通的 b 类文章的体量的话，我短时间还达不到这样的水平。

TorusE

paper: TorusE: Knowledge Graph Embedding on a Lie Group

论文

该文是日本 SOKENDAI 高等研究生院（相当于中科院研究生院）发表在 AAAI 2018 上的工作，文章提出了 TorusE。主要思想是：由于 TransE 的正则化（对 embedding 的归一化约束）与翻译规则 "h+r=t" 存在冲突，因此本文提出在紧密空间（compact space）中进行 embedding 来解决该问题。TransE 的归一化约束将 embedding 限制在球面，而 TorusE 提出了环形（甜甜圈形状的 torus），这样便不需要归一化。

说实话这篇文章我并没有看懂。感觉作者应该是学数学出身的吧，这个模型涉及到很多数论的概念，几乎不能理解，权当拓展下知识面，我也不会去做这方面的东西。首先我对文章提出的问题就模模糊糊的，并不确定该问题是否存在；再次，对于 TorusE 为什么能解决该问题也是完全没搞明白，唉… ==| 都说日本人在把东西讲得简明易懂这方面做得很好，但是从这篇论文我并没有感受到。

文献综述部分将模型进行了典型的三分类：翻译模型、双线性模型、神经网络模型。

TransE 的缺点及 embedding 空间要求

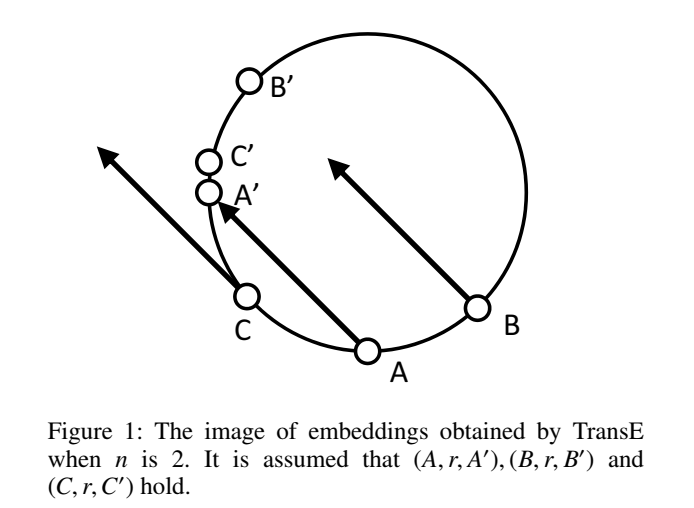
TransE 的归一化操作（限制 embedding 的范数为1）使得实体和关系被嵌入在向量空间的一个超球面上，它们的长度都是1，\(\Vert h \Vert=1\)，\(\Vert r \Vert=1\)，这种情况下，还要要求 \(\Vert h+r \Vert \leq 1\) 是不合理的，会导致训练出的 embedding 及链接预测的结果不精确。可能是我没有完全理解论文的意思，总觉得这种说法有待商榷。因为归一化不是限制范数等于1，而是小于等于1，embedding本身可以有大小，而且向量是有方向的，h+r的范数是有可能比h和t各自单独的范数都小的，所以论文提出的这个问题不一定在实际中存在（也可能是我还没有理解到位）。

为了解决文章提出的问题，需要一个新的 embedding 空间，从开放的流形（open manifold）转到紧密空间（compact space），文章给出的理由是：任何连续的实值函数在压缩空间中都是有界的，所以训练的 embedding 不会无限偏离，因此不需要正则化。

该紧密空间需要满足如下的几个条件：可微性、可计算性（可进行加减操作）、打分函数的可定义性。综上，阿贝尔李群（Abelian Lie Group）满足上述几个条件。

Lie Group 和 Torus

李群的定义：李群是一个有限维光滑流形群，其中乘和逆的群运算是光滑映射。TransE 的实值向量空间就是阿贝尔李群的一个例子，只是因为它的空间并不 compact，所以需要正则化。因此文章提出使用 torus，一个 compact 的李群。

torus 的定义：一个 n 维的 torus \(T^n\) 是一个商空间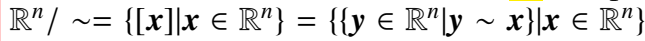，，其中 \(\sim\) 是等价关系。\(y\sim x\) 当且仅当 \(y-x \in Z^n\)。

从原始向量空间到 torus 空间的映射：

微分同胚映射指：在把两个光滑形状上的点等同起来的同时，也把对应的点处其他的光滑结构等同起来了。

定义了 torus 空间的三种距离函数：

第一种相当于向量空间的 L1 范数：

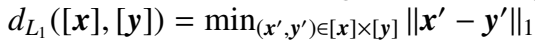
第二种相当于向量空间的 L2 范数：

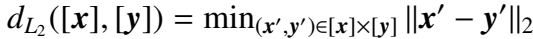
第三种：\(C^n\) 空间的 L2 范数：

TorusE

TorusE 仍然遵循翻译规则。对应 torus 上的三种距离函数定义了 TorusE 的三种打分函数：

1. \(f_{L_1}=2d_{L_1}([h]+[r],[t])\)

2. \(f_{L_2}=4d_{L_2}^2([h]+[r],[t])\)

3. \(f_{eL_2}=d_{eL_2}^2([h]+[r],[t])/4\)

当维度为1时，三种打分函数的曲线及其导数：

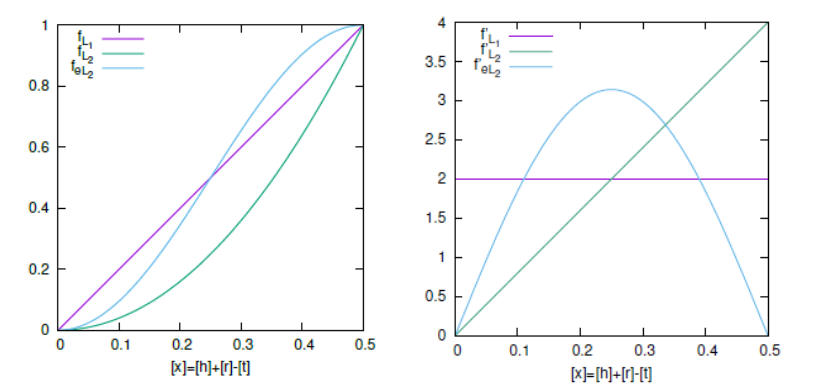
Loss：

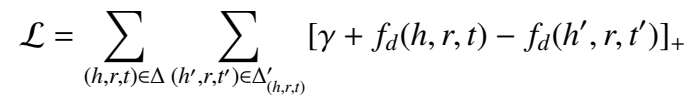
二维 torus 的 TorusE 如下图，

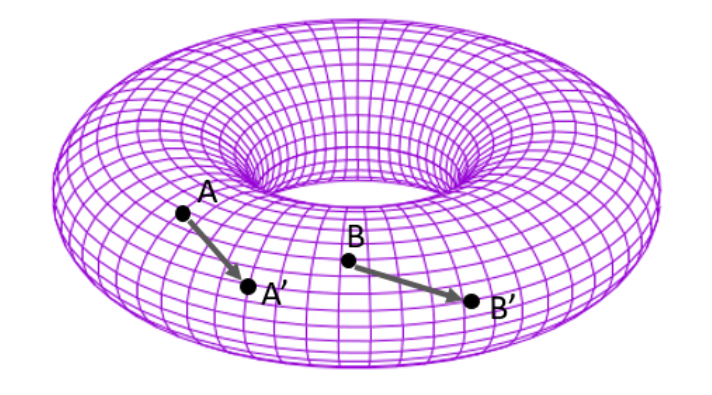
TransE 将 embedding 限制在球上（内），TorusE 将 embedding 限制在环形上，即可解决多个实体对共享同一关系的情况。（不懂=.=）

实验

严格的定量实验就只做了链接预测，为了显得充实，加入了评价 scalability 的实验。

1. scalability

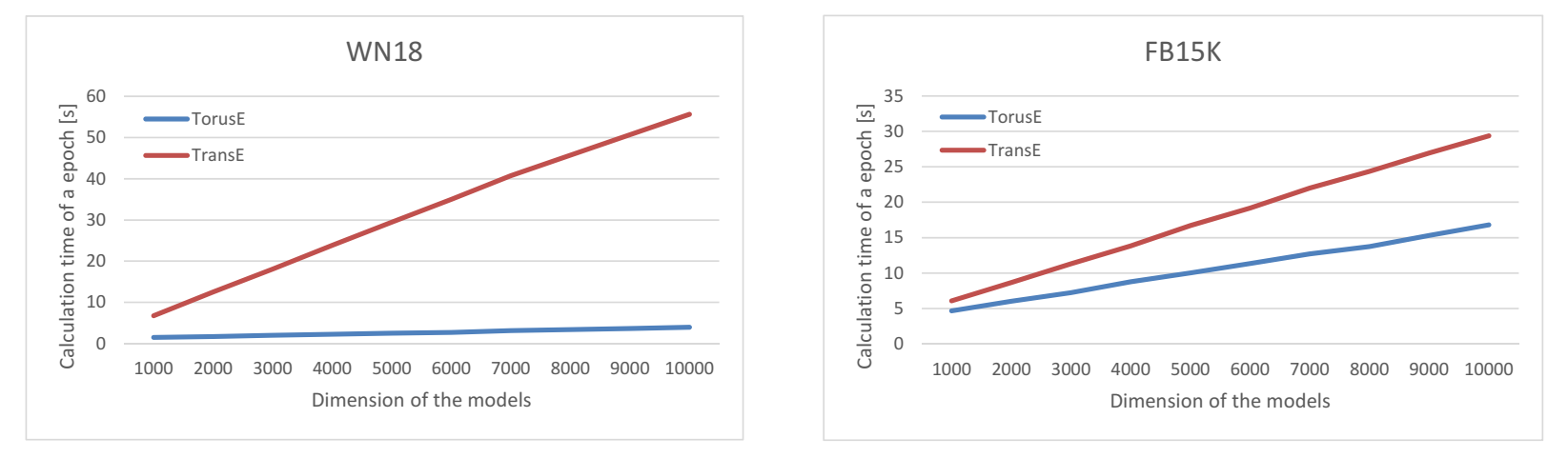
这部分实验是为了表明随着实验维度的增加，TorusE 计算量的增长远远小于 TransE 的计算量的增长，因为在高维情况下，TransE 的归一化操作会占据大量的计算资源。

2. 链接预测

TransE、TransR 模型在 Hits@1 效果很差，表明它们不擅长进行精确链接预测，而 TorusE 在 Hits@[1,3,10] 效果都很好。

代码

在 github 上找到了作者的源代码：https://github.com/TakumaE/TorusE ，是用 Tensorflow 实现的。

来学习一下核心的模型部分的实现。BasicModel 包括 embedding 的初始化、loss的计算及 testing score 的计算。TorusE 继承 BasicModel，唯一的不同就是打分函数的定义。

class TorusE(BasicModel):
    def __init__(self, config, nent, nrel):
        super(TorusE, self).__init__(config, nent, nrel)

    def scoring_func(self, h, r, t):
        d = tf.subtract(tf.add(h, r), t)      # h+r-t
        d = d - tf.floor(d)      # tf.floor 向下取整
        d = tf.minimum(d, 1.0 - d)
        if "el2" in self.config.reg:      # tf.reduce_sum 求和
            return tf.reduce_sum(2 - 2 * tf.cos(2 * math.pi * d), 1) / 4  # 4sin^2(pi*d)，推导得 g([x])-g([y])定义为 sin(pi*(h+r-t))
        elif "l2" in self.config.reg:
            return 4 * tf.reduce_sum(tf.square(d), 1)      # 4d^2(h,r,t)
        else:  # l1
            return 2 * tf.reduce_sum(tf.abs(d), 1)      # 2d(h,r,t)

此外，很多外围代码（包括数据处理、链接预测）值得借鉴。代码中还需要学习的一点是：它的 data 文件夹中是自己构建的几条用于 debug 的样本。在正式跑实验之前，可以不必用真正的数据集，可以自己构建几条数据，debug 无误后再上正式的数据集。

---

小结：
看不懂，就只记住它用了甜甜圈来进行 embedding 好了。

这两篇文章都比较复杂，看的时间也比较久，有些点不太好理解，但是能感觉到是比之前看论文更顺手了，已经知道怎样去关注重点、忽略不重要的细节，构建属于自己的知识体系。继续努力！