翻译模型（五）（PTransE、ManifoldE）
PTransE
paper: Modeling Relation Paths for Representation Learning of Knowledge Bases
论文
这篇文章是清华大学刘知远老师团队发表在 EMNLP 2015 上的工作，文章提出了对多跳关系路径进行建模的 PTransE（Path-based TransE）模型。之前的模型只针对实体间的单跳关系，该工作则可以挖掘实体间的多跳关系，可用于知识推理。
模型
两跳关系的 PTransE 如图所示：
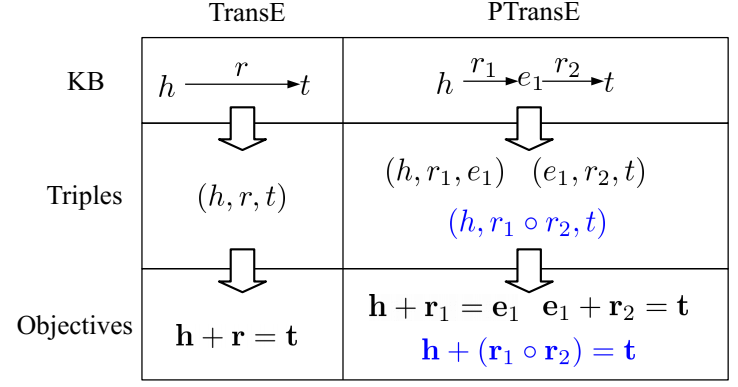
需要解决的两个问题是：关系路径的信度度量（Relation Path Reliability）和关系路径（组合）表示（Relation Path Representation）。
PTransE 定义的三元组的能量函数为：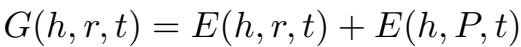 
其中， \(E(h,r,t)\) 为直接三元组得分， \(E(h,P,t)\) 为多跳路径三元组得分。
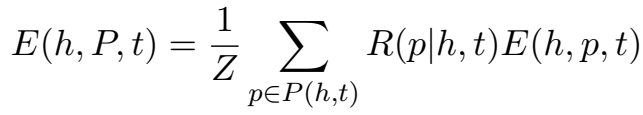
\(R(p|h,t)\) 为给定 h、r，路径 p 成立的信度，\(E(h,p,t)\) 为经过路径 p 的三元组得分，\(Z\) 为归一化项，\(Z=\)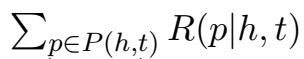 
下面分别介绍两个问题的解决，即打分函数中 \(R(p|h,t)\) 及 \(E(h,p,t)\) 如何计算。
关系路径信度度量
对于路径信度的度量，使用路径约束资源分配（path-constraint resource allocation，PCRA）的算法，该方法最初被用于个性化推荐。主要思想是：在图中，某种资源从头实体，通过路径 p 流向尾实体，用头实体通过该路径最终流到尾实体的资源量表示该路径的信度。
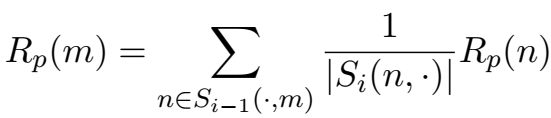
这里不详细解释符号了，大概意思就是，每个节点最初有一些资源（设为1），然后拿出一部分，平均分发给它的所有的一跳关系的节点，这样迭代下去，各个点的资源量就会达到某种平衡。这里，m 节点得到的资源量是它的所有前驱节点给它的资源之和。和信息检索中的 Page Rank 思想一样。
这虽然是一种度量路径信度的方法，但是如何解释为什么要使用它，以及为什么它可以度量路径的信度，论文中并没有明确说明。和很多神经网络模型一样，只是有效，却不知为何。
关系路径表示
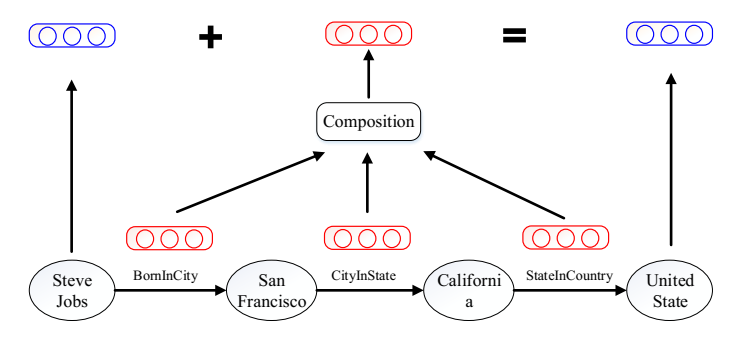
对于如何组合多跳关系的表示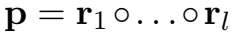
，文章提出了三种方式：
相加（ADD）: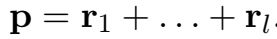 
相乘（MUL）：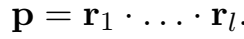 
循环神经网络（RNN）：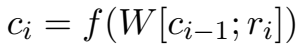 
RNN 是一个循环迭代操作，即 \(c_1=r_1\)，将后一个关系与前一个关系的 RNN 结果拼接，乘一个矩阵，过一个非线性函数，得到该关系之前的组合表示。
三元组打分函数及 Loss
仿照 TransE，定义给定关系 p 的三元组打分函数：
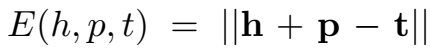
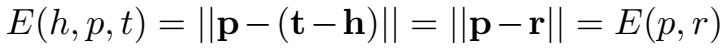
等同于路径 p 与关系 r 的相似性度量。
损失函数定义为： \(L(S) = \sum_{(h,r,t) \in S} [L(h,r,t) + L(p,t)]\)，包括直接三元组得分和多跳路径三元组得分两部分。两部分都是 margin-based 的 loss：
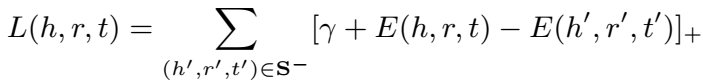
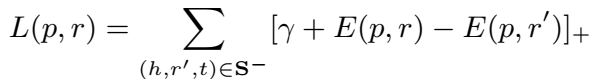
归一化约束还是保证实体和关系的 L2 范数小于等于1。
对应多个关系的实体，在多跳关系计算中会显著增加计算量，因此，实现时将路径限制在3跳，并选择信度在0.01以上的路径进行学习。
实验
进行了两个实验：链接预测和关系抽取。
- 知识库补全（链接预测）
链接预测使用的打分函数稍有不同，
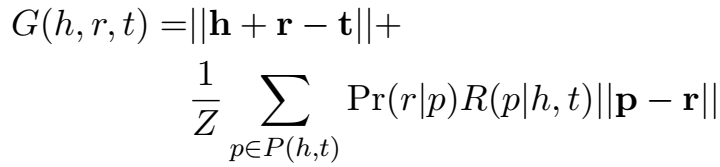
比前面的 \(E(h,p,t)\) 多了 \(P_r(r|p)\) 部分，这是由关系 r 决定的路径信度，因为文章认为 h 到 t 的路径信度不应当仅仅由头尾实体决定，因此加上由关系决定的部分。
由于实体预测阶段需要遍历所有的实体，多跳关系又显著增加了计算量，因此为了降低计算量，实验先取 TransE 结果的 top500，再用 PTransE 打分排序。
这部分实验分为实体预测和关系预测两部分。
实体预测结果（居然没有说是哪个数据集上的？应该是FB15k）：
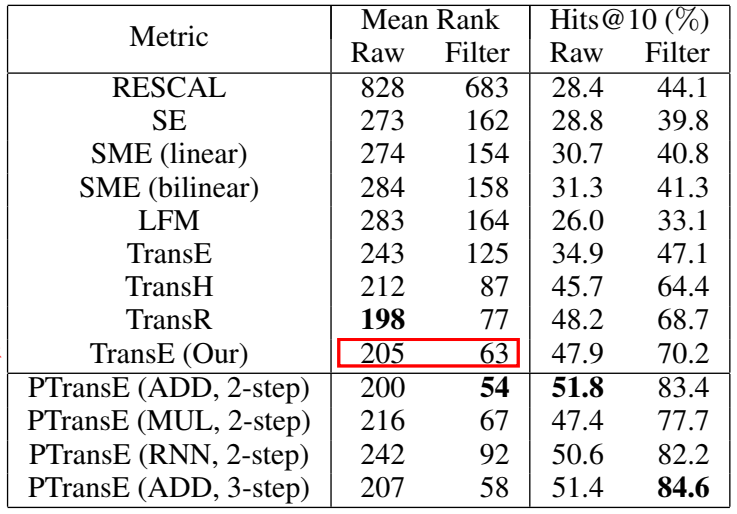
这里作者自己实现的 TransE 效果非常好，极具竞争力。不明白后面这些小修小补的 Trans 系列模型存在的意义是什么。
各关系类型下的实体预测结果：
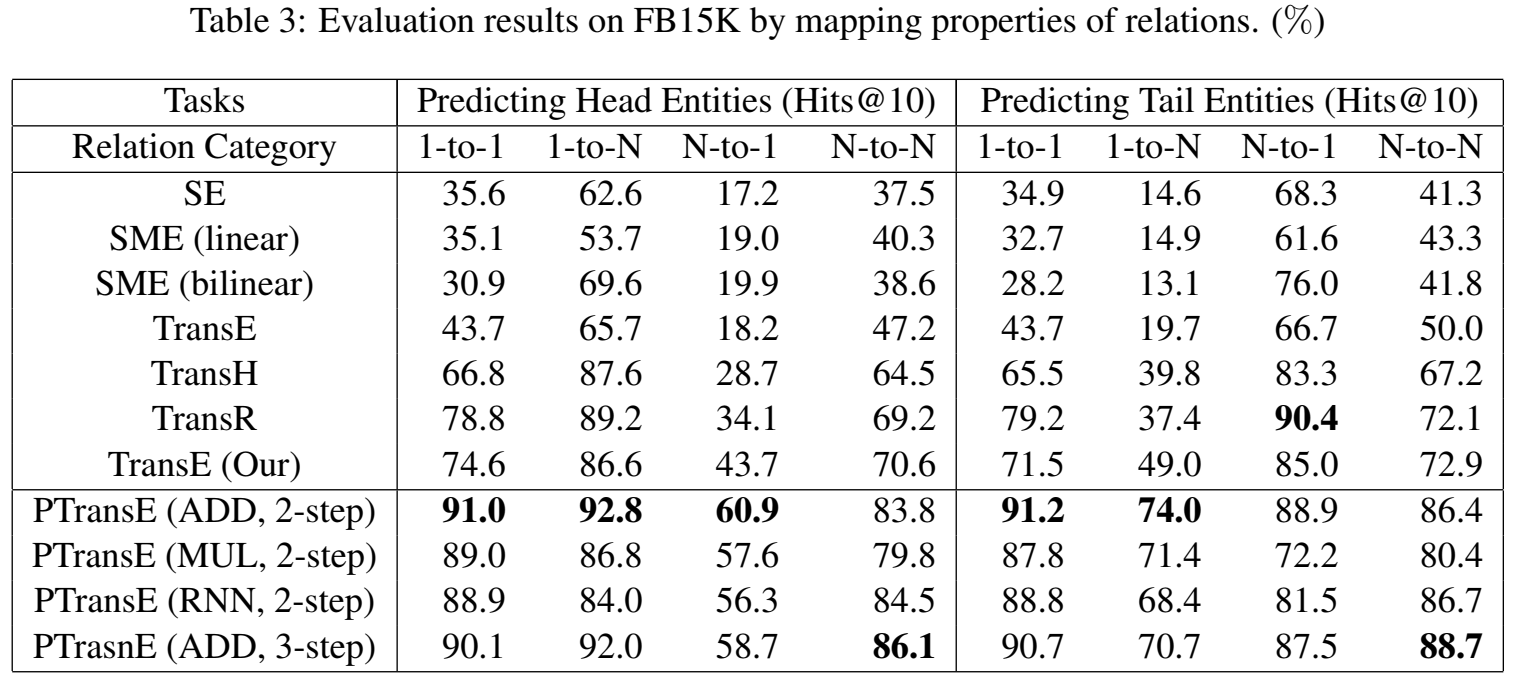
关系预测结果（FB15k）：
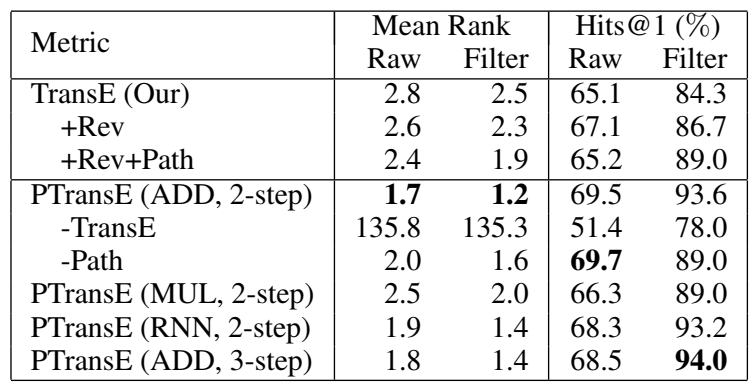
- 关系抽取
从纽约时报语料（NYT）中进行关系抽取。绘制 PR 曲线如下：
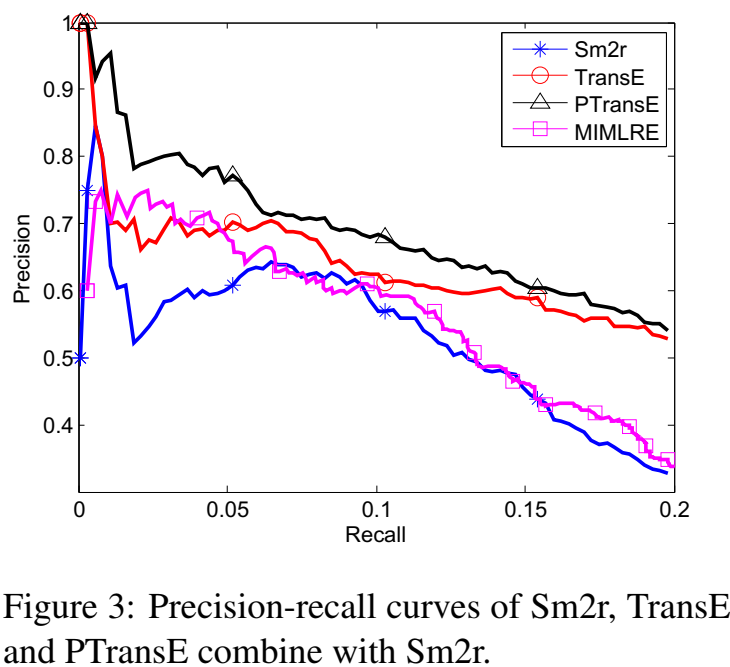
- case study
实验最后还进行了一个小的 case study，表明使用 PTransE 可以推断出新知识。
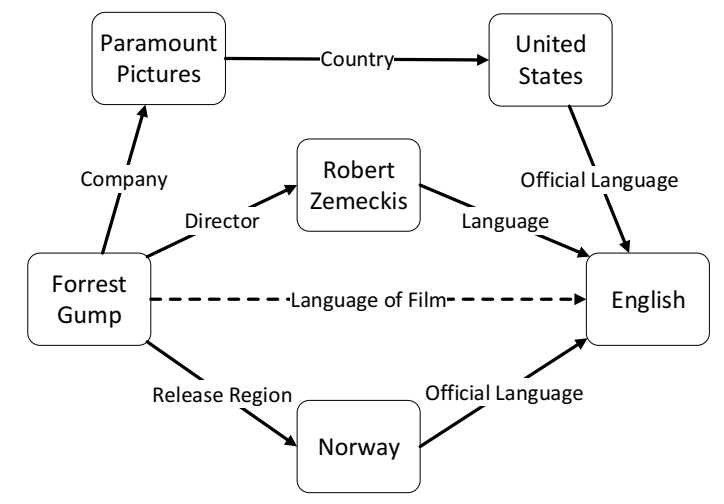
代码
OpenKE 和 Pykg2vec 没有实现，但作者提供了 C++ 版本的源码：https://github.com/Mrlyk423/Relation_Extraction/tree/master/PTransE 。此外作者还给出了 TransH、TransR/CTransR 的 C++ 实现。
其中，PCRA.py 是用于路径信度度量的资源分配算法的实现，是用 python 实现的。（瞄了一眼，全是for循环和if else，不禁感叹原来大神也写这种语句_|）
C++ 的实现就是比较琐碎，没有 python 框架那些比较直观。代码比较长，没有自己看，也不往上贴了，暂时应该用不到。
小结： PTransE 建模多跳关系的思想很有价值，并不像之前的 Trans 系列模型，只是在打分函数上小修小补。同时 PTransE 是一个可移植的模型，可迁移到 TransR、TransH 上形成 PTransR、PTransH（文章结论有提到）。私以为这是一篇有价值的文章，其中思想或可有落地实用的机会。
ManifoldE
paper: From One Point to a Manifold: Knowledge Graph Embedding for Precise Link Prediction
论文
这篇文章是清华大学朱小燕黄民烈老师团队发表在 IJCAI 2016 上的工作，提出了 ManifoldE，将传统的基于“点”的表示上升为“流形”表示，将表示头尾实体的“点”拓展为高维空间的“球”或“超平面”的表示，加“核”是流形表示的关键。
问题提出
文章首先提出了“精确链路预测（precise）”的问题：给定一个实体和一个关系，准确预测出另一个实体。文中说之前的模型只给出了候选答案，但我觉得严格来说这并不能单拎出来作为一个问题，之前模型预测结果的 Hits@1 其实给出的就是精确的预测结果。文中说造成该问题的原因有两个：ill-posed algebraic system 和 over strict geometric form。（为什么我感觉驴唇不对马嘴，有种“静静看着你zb”的感觉，对不起作者，科研应当严肃！）
ill-posed algebraic system 问题指的是变量的数量少于方程式的数量，这会导致问题的解不精确和不稳定。为了解决该问题，文章设定 embedding 的维度 \(d\geq \frac{训练样本数}{实体数+关系数}\)。over strict geometric form 问题指的是向量表示不足以建模复杂关系，因此文章将基于点的位置表示扩展到流形空间（如高维球体）。
ManifoldE
流形表示的基础是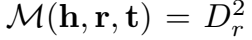 
，即用半径为 Dr 的球体范围表示三元组的得分范围，直白一点来说就是放大了 (h+r-t) 能接受的误差范围，本来应该是 h+r-t=0 是 golden triplet，现在 -Dr<=h+r-t<=Dr 的都是 golden triplet。
该模型下的三元组打分函数为:
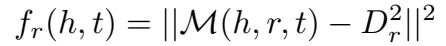
Dr 是与关系 r 有关的流形参数，M 是流形函数。根据 M(h,r,t) 的不同，提出了 Sphere 和 Hyperplane 两种流形 embedding 方式。
Sphere
在球形模式下，流形函数定义为：
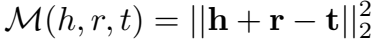
对于给定的 h 和 r，正确的尾实体 t 被限制在一个球（而非点）内。这种情况下，当 Dr=0 时，模型退化为 TransE。
通过加核操作，将实体和关系引入再生核希尔伯特空间（Reproducing Kernel Hilbert Space，RKHS）（希尔伯特空间指含蓄的高维空间）。
\(\phi\) 是从原始空间到希尔伯特空间的映射，\(K\) 是核，可以是线性核、高斯核、多项式核等。
Hyperplane
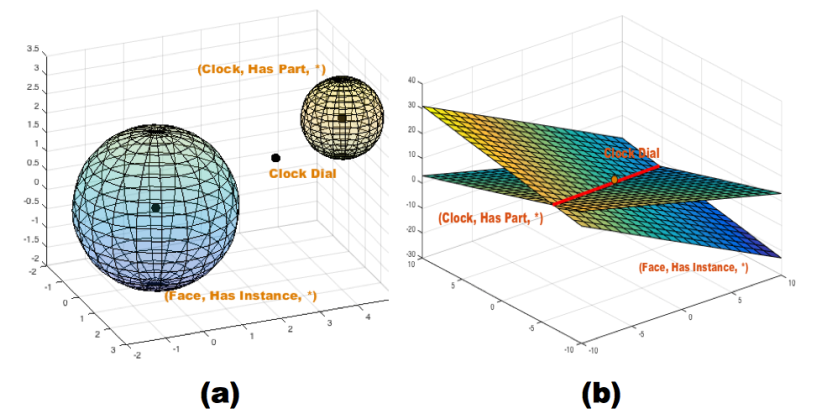
如上图， "Clock Dial"在理想情况下应同时存在于两个球体中（因其同时满足两个三元组），但两个球没有交叉（为什么不可以通过训练使两个球相交？），无法解决这个问题，因此提出了 Hyperplane 的 Manifold，M 函数定义如下：
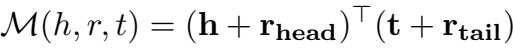
因为只要两个平面不平行，它们就会相交，即可解决图中的问题。对于给定的 h 和 r， 尾实体位于方向为 \(h+r_{head}\) 的超平面上，可以有 \(D_r^2\) 的偏差。
【小疑问：】我觉得这里 M 的定义应该加负号，因为正三元组的 t 和 h+r 是不正交的，因此得分是偏大的，负样本的得分较小。
加核的流形函数为：
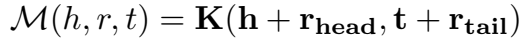
文章还从代数和几何两个角度解释了 Manifold 的好处，言之无物。
Loss 和其他一样，都是 margin-based 的：
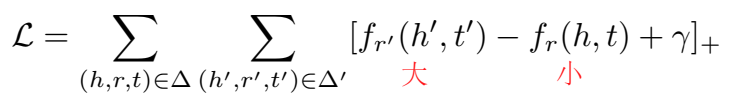
优化器使用 SGD。
实验
进行了链接预测和三元组分类实验。
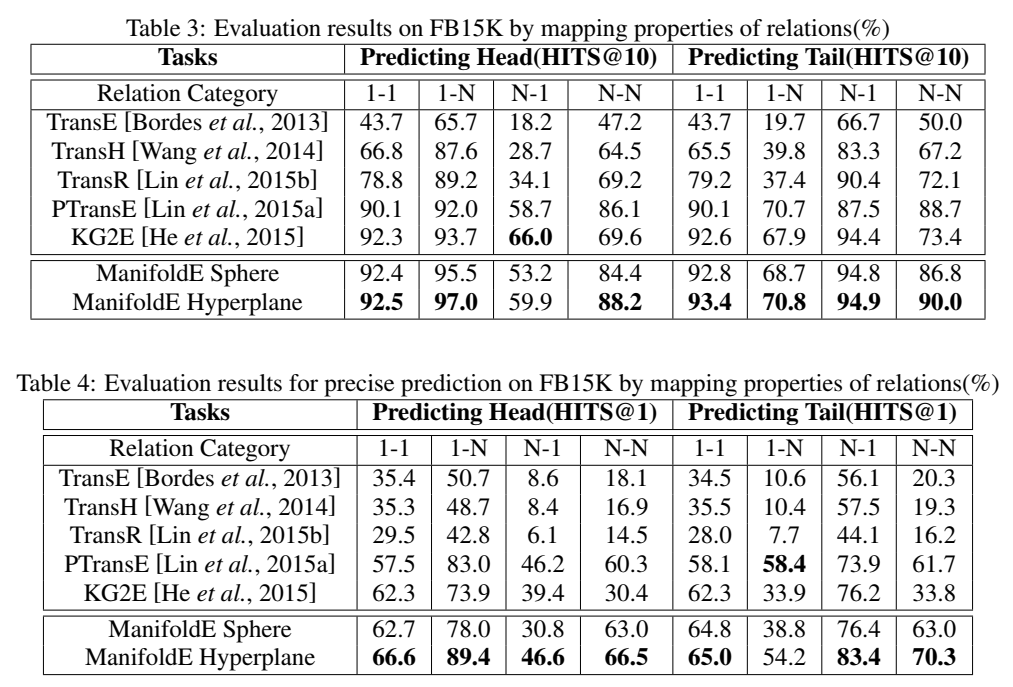
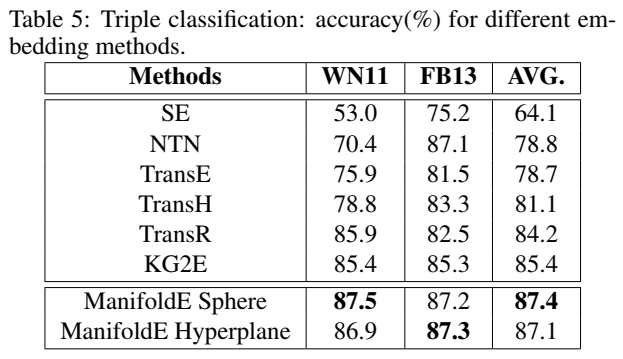
没有找到代码。
小结： 这篇文章看起来很玄乎，很多概念的东西，但总给我一种强行拉扯的感觉，读完之后总感觉没有那么透彻地弄明白。真的不明白为什么它提出的模型可以解决它提出的问题。
