翻译模型（四）（TransF、TransM、SSE）
这篇博客介绍 TransF、TransM 和 SSE，也都是比较老的模型了。
TransF
paper: Knowlege Graph Embedding by Flexible Translation
论文
这篇论文是清华大学黄民烈朱小燕老师团队发表在 AAAI 2015 上的文章（其实并不确定，因为没有找到正式发表的信息，只在百度学术上的引用中有 AAAI Press 的字样）。文章提出了 TransF 模型，F 代表 flexible，采用了 "flexible translation" 的思想来进一步解决 1-n、n-1、n-n、reflexive 这样的复杂关系表示的问题。具体说，就是用 "h+r≈αt" 代替比较 hard 的 "h+r≈t"，即只要保证 "h+r" 的方向与 t 的方向相同即判定三元组 (h,r,t) 成立。思想非常简单，模型并不复杂，但不得不说这种设计还是非常巧妙的。
模型思想
-
对于自反关系，有 h+r=t 和 t+r=h 同时成立，得出 r=0，h=t，显然不合理，TransF 的解决方法是：令 \(h=\frac{2}{\alpha_1\alpha_2-1}r\)，\(t=\frac{\alpha_2+1}{\alpha_1\alpha_2-1}r\)，这样便可得 \(h+r\approx \alpha_1t\)，\(t+r\approx \alpha_2h\)（但我并没有推导出这样的结果）。
-
对于 1-n 关系，令 \(t_0=\frac{h+r}{\alpha_0}\)，…，\(t_n=\frac{h+r}{\alpha_n}\)。
-
对于 n-1 关系，令 \(h_0=\alpha_0t-r\)，…，\(h_n=\alpha_nt-r\)。
打分函数及 loss
打分函数本应是这样的：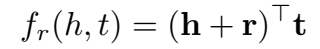
，计算 \(h+r\) 与 \(t\) 的点积，但这样的打分函数存在如下的问题：
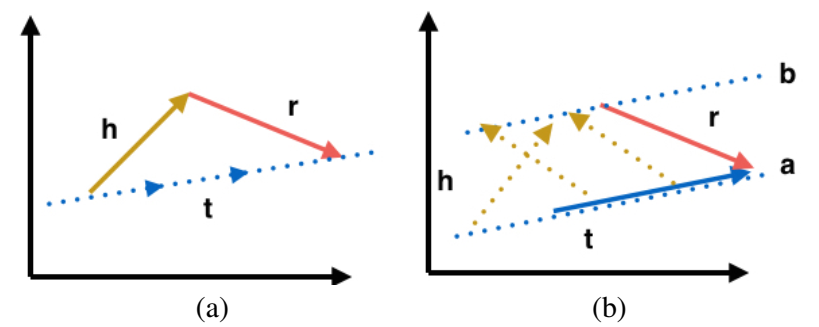
给定 h 和 r，t 的范围被限制在一条线（一个向量方向）上，而给定 t 和 r，则 h 的方向与长度可以任意，只要满足是从线段 a 的某一点指向线段 b 的某一点的向量即可。为了保证 h 和 t 有同样的约束，将上述的打分函数对称化一下：
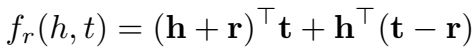
正样本得分高，负样本得分低，因为正交向量点积为 0，正样本的 h+r 应当与 t 平行（不正交），之前模型都是正样本的得分接近0，负样本的得分高，因此这里的损失函数的定义也与之前相反：
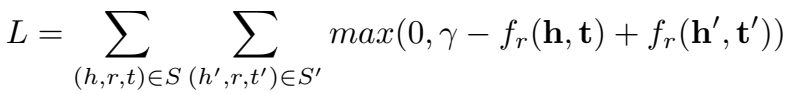
训练使用 SGD 优化。
TransRF
TransF 的方法可以移植到其他模型，文章移植到了 TransR，提出 TransRF：
实验
除了常规的链接预测和三元组分类实验，文章还对样本的分数分布进行了可视化分析。
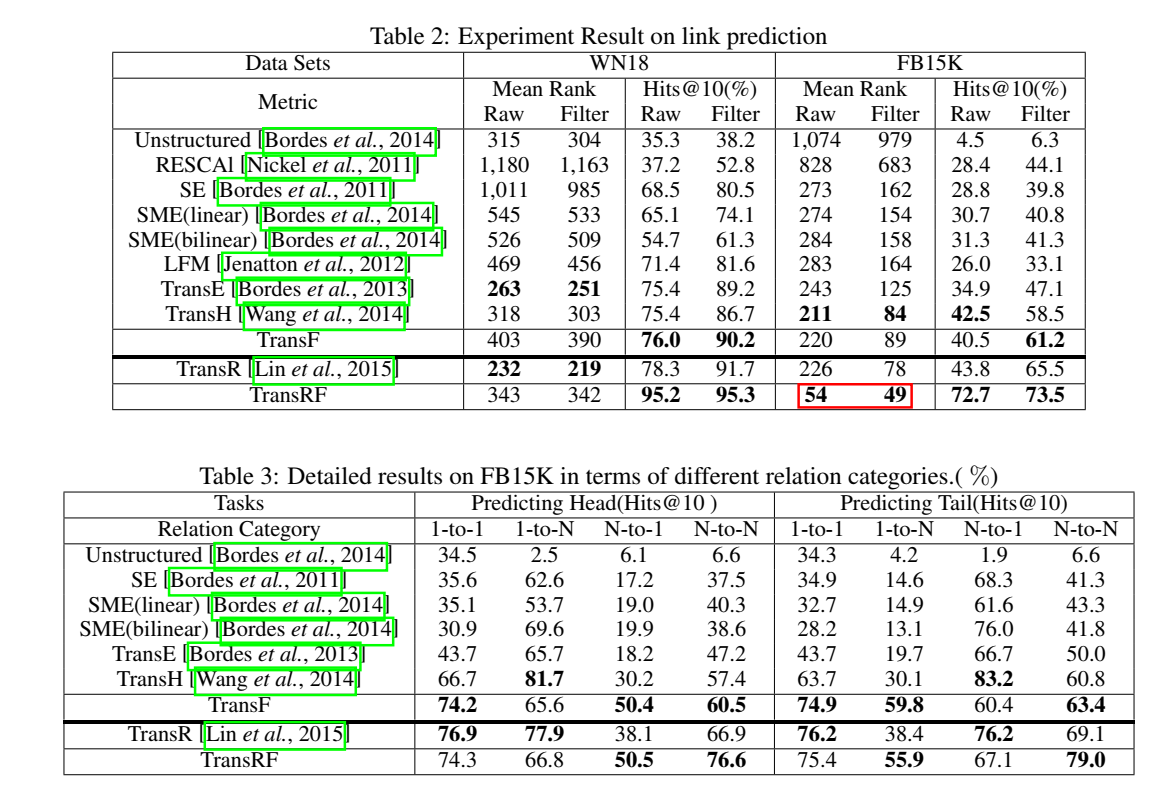
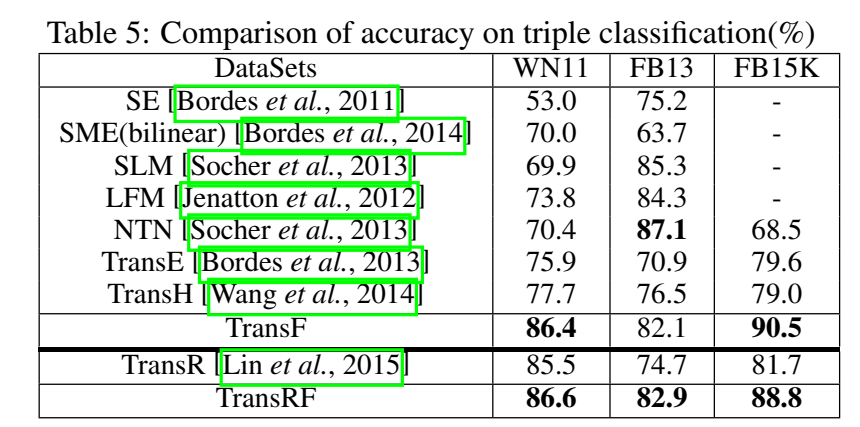
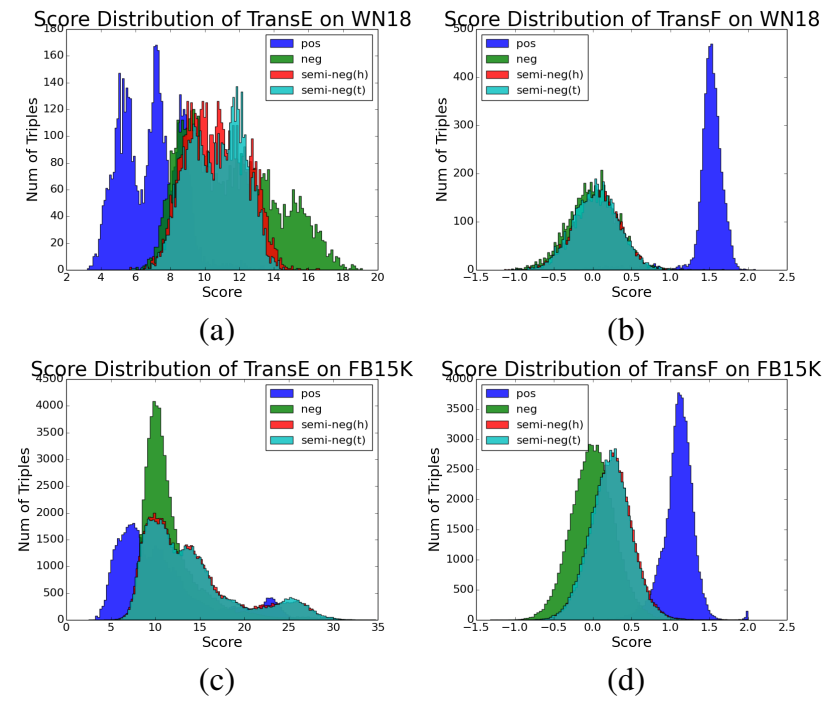
从前两个实验的结果来看，TransF的提升并不算显著，但是其定义的打分函数却能很好地将正负样本区分开。
没有找到 TransF 的代码，openKE 和 Pykg2vec 都没有实现，github上也没有，TransF 应该是 Trans 系列里比较冷门的一个模型了。
小结：早期跟进 TransE、在 Trans 系列上做文章的也就那么三个主要的团队：清华大学刘知远老师、清华大学黄民烈朱小燕老师、自动化所赵军刘康老师，各个团队的模型风格也大概有所了解有一点感觉了。刘知远老师团队的工作比较硬核，自动化所赵军老师组的工作比较扎实、细致，黄民烈朱小燕老师组的模型工作量不大，但在写作上有巧妙之处。后续看下新的模型有没有这三个团队做的工作。
TransM
paper: Transition-based Knowledge Graph Embedding with Relational Mapping Properties
论文
该文是清华大学（不知道哪个团队）和埃默里大学共同发表在 PACLIC（CCF 列表上没有找到这个会，大概相当于C的水平） 2014 上的文章，提出了 TransM，M 代表 mapping。文章是在 TransE 后的第二年出的，还没有 TransH 和 TransR，所以 baseline 只对比了 TransE 和一些非 Trans 模型。
模型
模型的思想非常简单，就是在计算得分时为每个三元组赋一个预计算的权重，该权重反映了该关系下的实体节点的度。
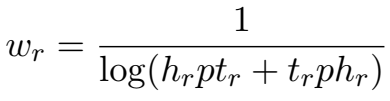
根据权重的计算公式，对于 1-n、n-1 等实体密度比较大的三元组，赋予比较小的权重，其三元组打分会偏低。这样，"1-1" 类关系会比复杂关系类型有更为严格的限制。
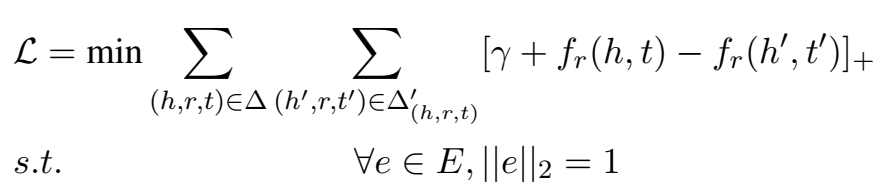
实验
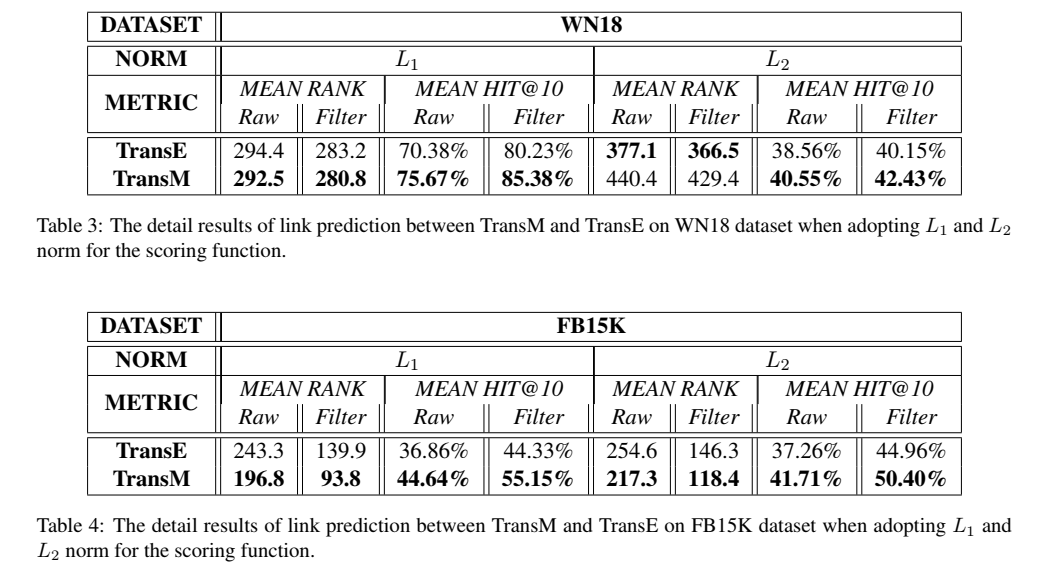
实验进行了链接预测和三元组分类。
- 链接预测
与 TransE 的链接预测结果对比，使用了 L1 范数和 L2 范数，L1 范数的效果普遍比 L2 效果好。
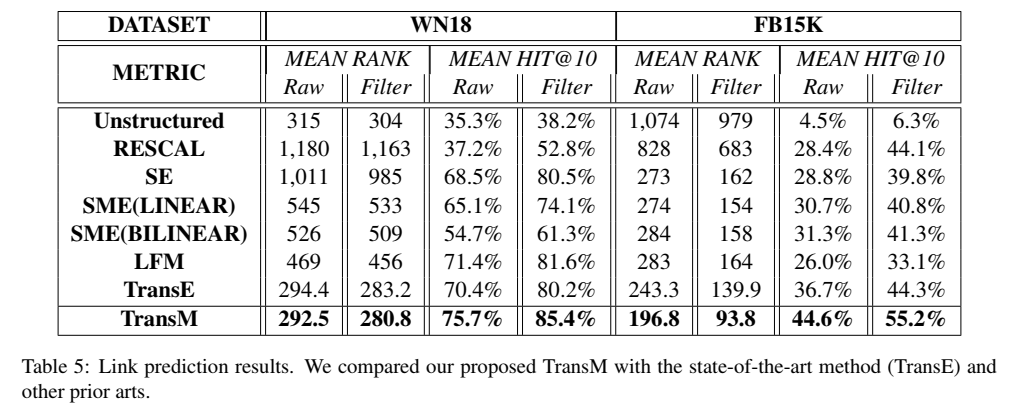
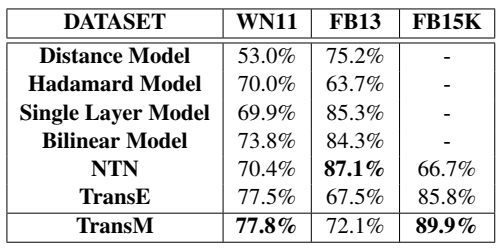
与其他模型的对比：
区分关系类型的模型效果：
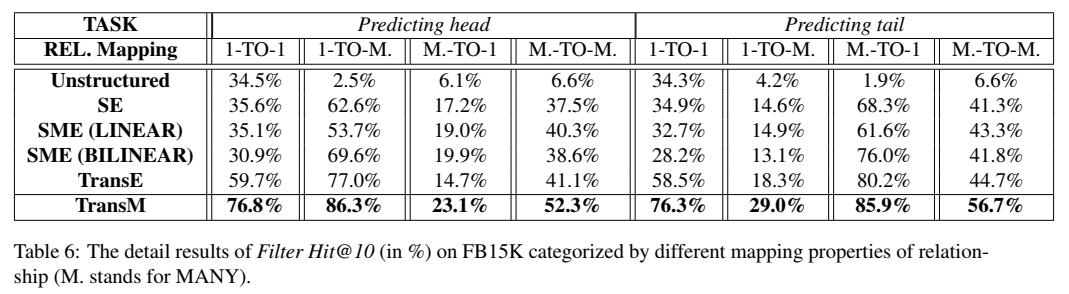
- 三元组分类
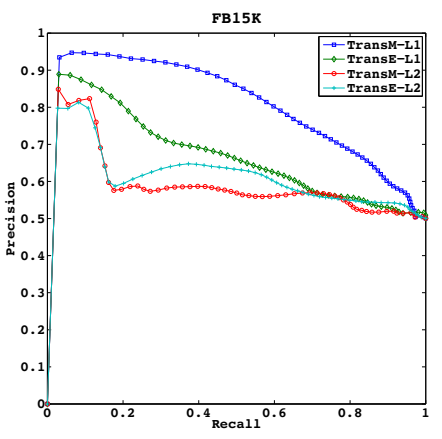
还画出了三元组分类的 PR 曲线：
代码
上 \(Pykg2vec\) 的实现：
class TransM(PairwiseModel):
def __init__(self, **kwargs):
super(TransM, self).__init__(self.__class__.__name__.lower())
param_list = ["tot_entity", "tot_relation", "hidden_size", "l1_flag"]
param_dict = self.load_params(param_list, kwargs)
self.__dict__.update(param_dict)
self.ent_embeddings = NamedEmbedding("ent_embedding", self.tot_entity, self.hidden_size)
self.rel_embeddings = NamedEmbedding("rel_embedding", self.tot_relation, self.hidden_size)
rel_head = {x: [] for x in range(self.tot_relation)}
rel_tail = {x: [] for x in range(self.tot_relation)}
rel_counts = {x: 0 for x in range(self.tot_relation)}
train_triples_ids = kwargs["knowledge_graph"].read_cache_data('triplets_train')
for t in train_triples_ids:
rel_head[t.r].append(t.h)
rel_tail[t.r].append(t.t)
rel_counts[t.r] += 1
# "heads per tail 每个尾巴有几个头" hpt = rel_counts[x]/(1+len(rel_tail[x]))
# "tails per head 每个头有几个尾巴" tph = rel_counts[x]/(1+len(rel_head[x]))
theta = [1/np.log(2 + rel_counts[x]/(1+len(rel_tail[x])) + rel_counts[x]/(1+len(rel_head[x]))) for x in range(self.tot_relation)]
self.theta = torch.from_numpy(np.asarray(theta, dtype=np.float32)).to(kwargs["device"])
nn.init.xavier_uniform_(self.ent_embeddings.weight)
nn.init.xavier_uniform_(self.rel_embeddings.weight)
self.parameter_list = [
self.ent_embeddings,
self.rel_embeddings,
]
self.loss = Criterion.pairwise_hinge
def forward(self, h, r, t):
"""Function to get the embedding value.
Args:
h (Tensor): Head entities ids.
r (Tensor): Relation ids.
t (Tensor): Tail entity ids.
Returns:
Tensors: the scores of evaluationReturns head, relation and tail embedding Tensors.
"""
h_e, r_e, t_e = self.embed(h, r, t)
norm_h_e = F.normalize(h_e, p=2, dim=-1)
norm_r_e = F.normalize(r_e, p=2, dim=-1)
norm_t_e = F.normalize(t_e, p=2, dim=-1)
r_theta = self.theta[r]
if self.l1_flag:
return r_theta*torch.norm(norm_h_e + norm_r_e - norm_t_e, p=1, dim=-1)
return r_theta*torch.norm(norm_h_e + norm_r_e - norm_t_e, p=2, dim=-1)
def embed(self, h, r, t):
"""Function to get the embedding value.
Args:
h (Tensor): Head entities ids.
r (Tensor): Relation ids of the triple.
t (Tensor): Tail entity ids of the triple.
Returns:
Tensors: Returns head, relation and tail embedding Tensors.
"""
emb_h = self.ent_embeddings(h)
emb_r = self.rel_embeddings(r)
emb_t = self.ent_embeddings(t)
return emb_h, emb_r, emb_t
自己跑模型的过程中，感觉 TransM 虽然是个名不见经传的冷门模型，但效果居然还不错，能超过 TransE 和 大多数非 Trans 模型。
小结： 虽然是个简单的 idea，但是效果却出奇地好，值得一篇 C。
SSE
paper: Semantically Smooth Knowledge Graph Embedding
论文
这篇文章是王斌和王泉老师还在信工所时，他们的团队发表在 ACL 2015 上的工作。文章提出了 SSE（Semantically Smooth Embedding），本质是在目标函数中加的两种约束项，使得属于同种类别的实体在 embedding 空间中的位置相近（即保证语义平滑）。两种约束项 LE（Laplacian Eigenmaps）和 LLE（Locally Linear Embedding）是起源于流形学习的两个算法，名字听起来比较高大上，实则思想很简单。
文章中对 KGE 本质的描述我觉得很到位，记录一下：KGE 分为三步，1) 表示实体和关系（定义表示）；2) 定义打分函数；3) 学习表示（训练）。不同模型的不同之处主要在于前两点：实体/关系表示的定义和能量函数的定义。
LE （Laplacian Eigenmaps）
借鉴 LE 思想的平滑假设：如果两个实体属于相同的语义类别，那么它们的 embedding 距离是相近的。
衡量 embedding 空间平滑度的约束项：
其中，\(w_{ij}\) 是邻接矩阵，标识两个实体是否属于同一类别。
加约束项的目标函数：
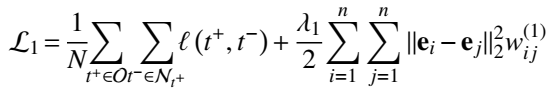
LLE（Locally Linear Embedding）
基于 LLE 思想的平滑假设：实体可以由其最近邻居表示，最近邻居代表同一类别的实体。
度量 embedding 空间平滑性的重构误差：
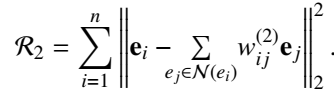
作为正则项加入 Loss：
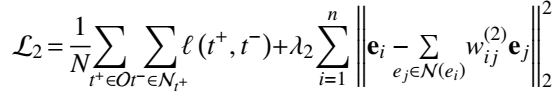
实验
- 链接预测
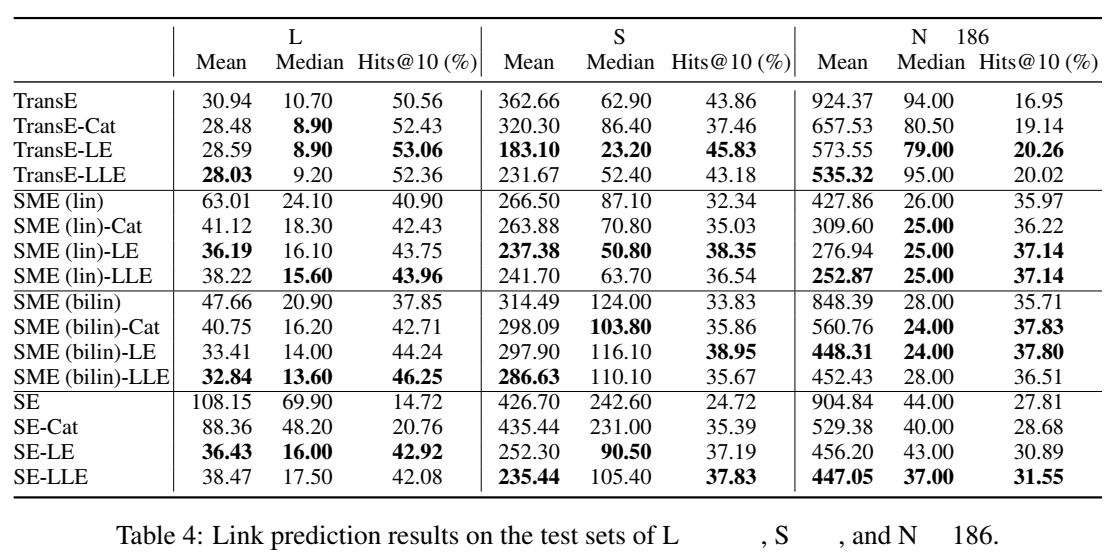
数据集使用 NELL 的三个子数据集，探究了加入类别编码、LE 和 LLE 三种机制的 TransE、SME（线性和双线性）、SE 四个模型的效果提升，没有对比 TransH 和 TransR。
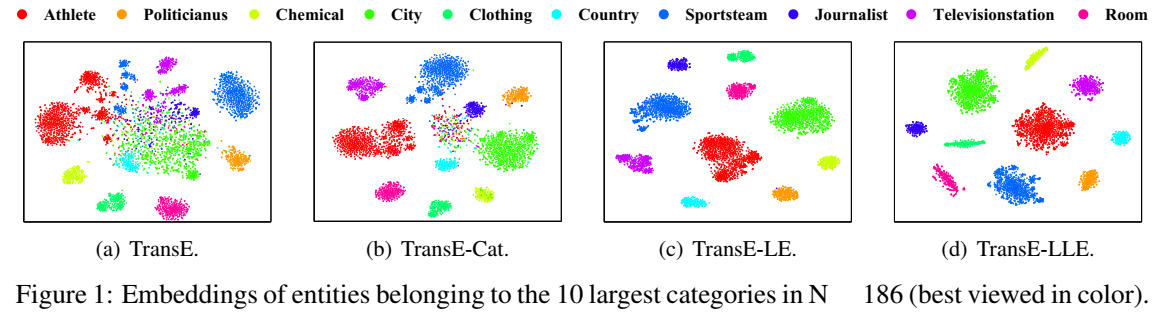
并用 t-SNE 对实体进行了降维可视化，表明加入 LE 和 LLE 能很好地将不同类别的实体在 embedding 空间中区分开。（有空应当学一下 t-SNE，感觉用的还挺多的，补充一下可视化方面的空白。）
- 三元组分类
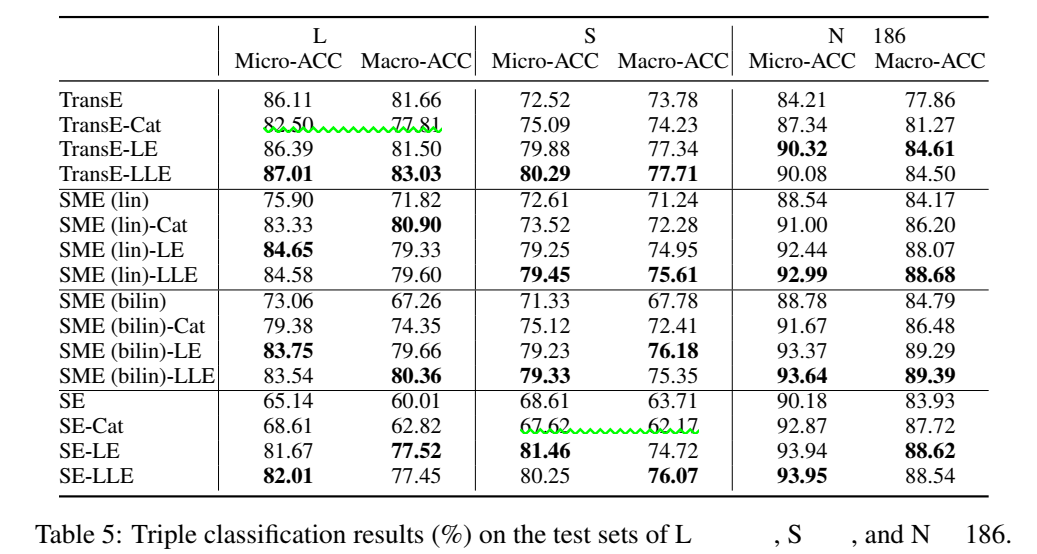
没有找到代码，用这篇文章思想的人应该不多吧。
小结： 其实严格来说 SSE 不算一个单独的模型，只是在其他模型（TransE）的基础上加了两个保证语义平滑的约束项，算是一个提升模型效果的小 trick。为了证明这两个约束项的有效性，在现有的模型上进行了对比试验，工作量还是比较充实的。虽然号称是来自于 manifold learning 的两个平滑思想，但本质十分 naive，不难理解。
