翻译模型(二)(TransD、TransA、TranSparse)
这篇整理 TransD、TransA、TranSparse,也都是之前看过的,比较熟悉。
TransD
paper: Knowledge Graph Embedding via Dynamic Mapping Matrix
论文
本文是自动化所赵军、刘康老师团队发表在 ACL 2015 上的工作,D 代表 Dynamic,是针对 TransR 参数量太大做的改进。主要思想是:实体和关系共同构建投影矩阵。具体地,每个实体和关系由两个向量(meaning vector 和 projection vector)表示,一个表示本身的 embedding,另一个用于构建投影矩阵。每个“实体-关系”对使用的投影矩阵是不同的,头尾实体单独投影。
构建投影矩阵
投影矩阵: 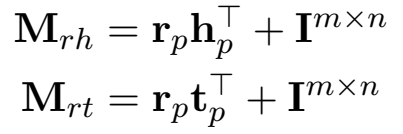
投影操作: 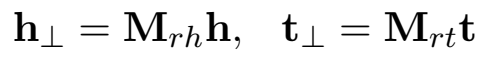
三元组打分函数: 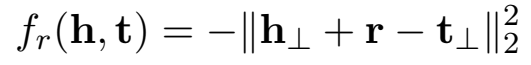
归一化约束和之前的模型一样,都是 \(\lVert \cdot \rVert_2 \leq 1\)。
Loss: 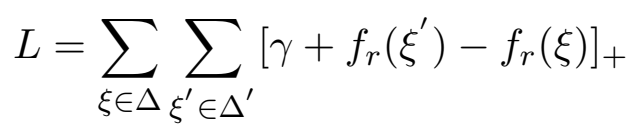
训练优化器使用 ADADELTA SGD,并使用 TransE 的训练结果初始化。
与 TransE、TransH 和 TransR 的关系
- 与 TransE 的关系
当实体、关系维度相同且所有的投影向量设为 0 时,退化为 TransE
- 与 TransH 的关系
当实体、关系维度相同时,TransD 的投影操作可展开为:

而 TransH 的投影操作为:
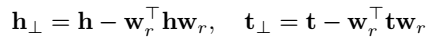
区别是,TransH 的投影向量仅由关系决定,而 TransD 的投影向量由实体和关系共同决定。
- 与 TransR 的关系
TransR 为每个关系训练一个投影矩阵 \(M_r\),TransD 通过投影向量动态地构建投影矩阵,没有“矩阵-向量”相乘的操作,大大减少了参数量和计算量。据原文称,TransD 比 TransR 快约三倍。
实验
文章进行了三元组分类和链接预测两个实验,并通过 case study 说明投影向量的属性。

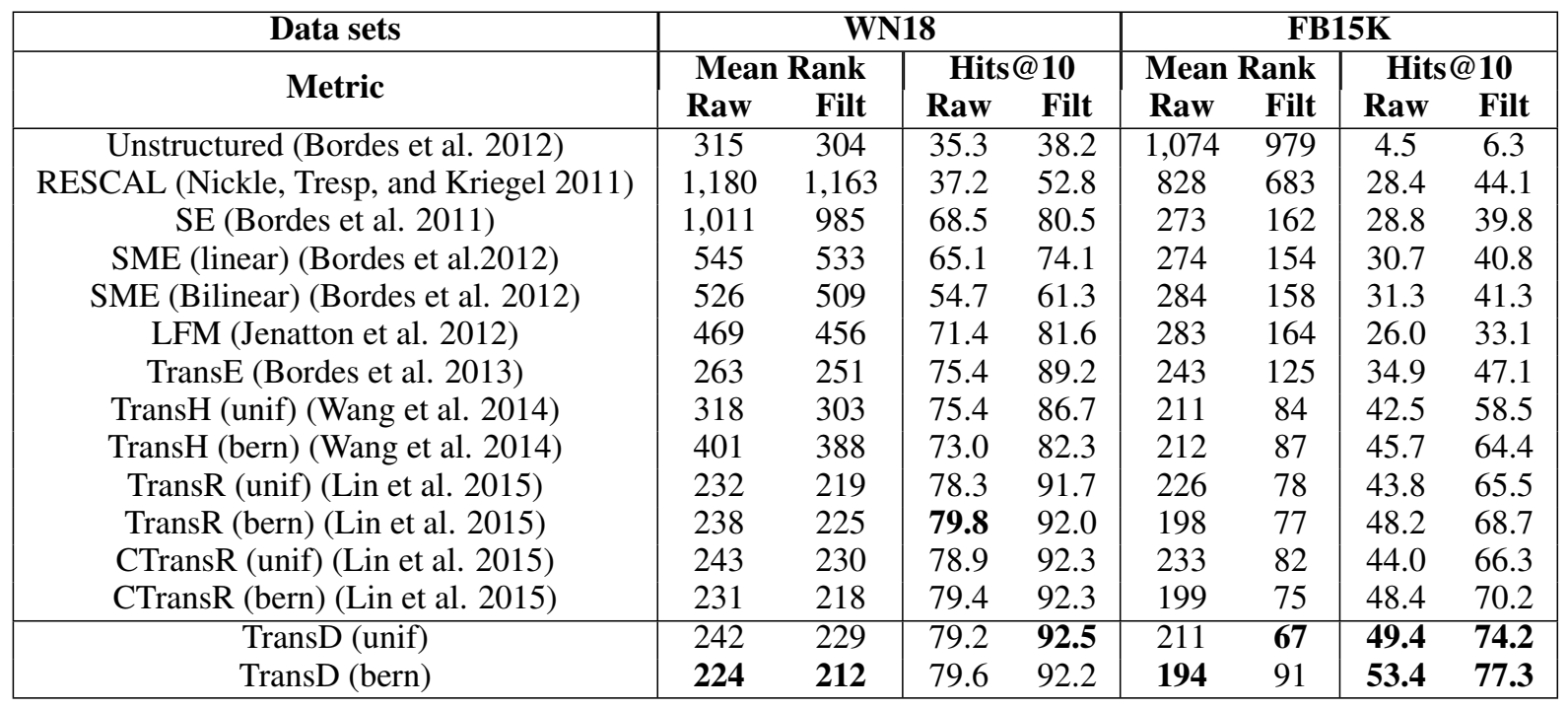

TransD 仍然是对打分函数的改进,然后赋予一个合理的物理意义,没什么新意。感觉 TransE 后续的这些系列模型全是中国人提出来的,总感觉是在蹭热度。用最新的东西、最新的噱头,因为跟进的人很少,所以不太可能会有很多人提出质疑,学到了。
TransH、TransR、TransD 都是在投影操作上下文章的,后面的就不是了。
代码
还是贴 \(Pykg2vec\) 的代码:
class TransD(PairwiseModel):
def __init__(self, **kwargs):
super(TransD, self).__init__(self.__class__.__name__.lower())
param_list = ["tot_entity", "tot_relation", "rel_hidden_size", "ent_hidden_size", "l1_flag"]
param_dict = self.load_params(param_list, kwargs)
self.__dict__.update(param_dict)
self.ent_embeddings = NamedEmbedding("ent_embedding", self.tot_entity, self.ent_hidden_size)
self.rel_embeddings = NamedEmbedding("rel_embedding", self.tot_relation, self.rel_hidden_size)
self.ent_mappings = NamedEmbedding("ent_mappings", self.tot_entity, self.ent_hidden_size)
self.rel_mappings = NamedEmbedding("rel_mappings", self.tot_relation, self.rel_hidden_size)
nn.init.xavier_uniform_(self.ent_embeddings.weight)
nn.init.xavier_uniform_(self.rel_embeddings.weight)
nn.init.xavier_uniform_(self.ent_mappings.weight)
nn.init.xavier_uniform_(self.rel_mappings.weight)
self.parameter_list = [
self.ent_embeddings,
self.rel_embeddings,
self.ent_mappings,
self.rel_mappings,
]
self.loss = Criterion.pairwise_hinge
def embed(self, h, r, t):
"""Function to get the embedding value.
Args:
h (Tensor): Head entities ids.
r (Tensor): Relation ids of the triple.
t (Tensor): Tail entity ids of the triple.
Returns:
Tensors: Returns head, relation and tail embedding Tensors.
"""
emb_h = self.ent_embeddings(h)
emb_r = self.rel_embeddings(r)
emb_t = self.ent_embeddings(t)
h_m = self.ent_mappings(h)
r_m = self.rel_mappings(r)
t_m = self.ent_mappings(t)
emb_h = self._projection(emb_h, h_m, r_m)
emb_t = self._projection(emb_t, t_m, r_m)
return emb_h, emb_r, emb_t
def forward(self, h, r, t):
"""Function to get the embedding value.
Args:
h (Tensor): Head entities ids.
r (Tensor): Relation ids.
t (Tensor): Tail entity ids.
Returns:
Tensors: the scores of evaluationReturns head, relation and tail embedding Tensors.
"""
h_e, r_e, t_e = self.embed(h, r, t)
norm_h_e = F.normalize(h_e, p=2, dim=-1)
norm_r_e = F.normalize(r_e, p=2, dim=-1)
norm_t_e = F.normalize(t_e, p=2, dim=-1)
if self.l1_flag:
return torch.norm(norm_h_e + norm_r_e - norm_t_e, p=1, dim=-1)
return torch.norm(norm_h_e + norm_r_e - norm_t_e, p=2, dim=-1)
@staticmethod
def _projection(emb_e, emb_m, proj_vec):
# [b, k] + sigma ([b, k] * [b, k]) * [b, k]
return emb_e + torch.sum(emb_e * emb_m, axis=-1, keepdims=True) * proj_vec
TransA
paper: TransA: An Adaptive Approach for Knowledge Graph Embedding
论文
该文是清华大学朱小燕黄民烈老师团队发表在 AAAI 2015 上的文章, A 代表 Adaptive。主要创新只有一点:将三元组打分函数中的欧氏距离改为马氏(Mahalanobis)距离(即加权的欧式距离)。论文提出的方法倒没有什么,倒是其他地方有很多值得学习的地方。
Adaptive Metric 打分函数
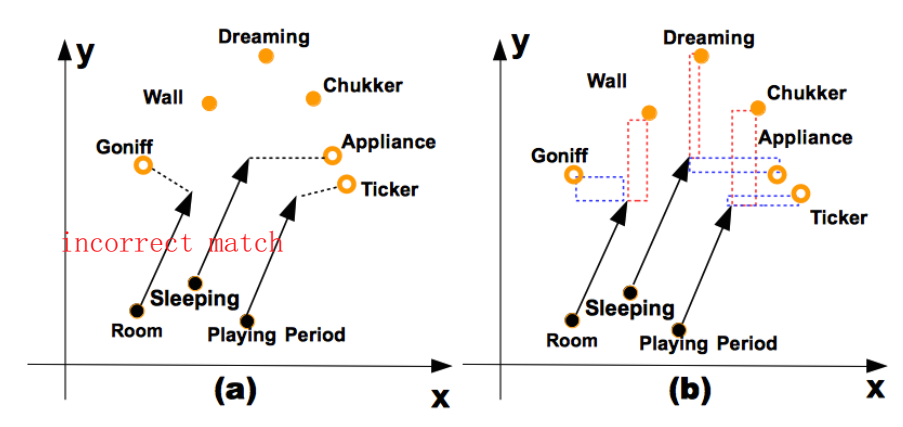
上图为对 TransA 的说明,大意就是,如果按照图(a)按照欧氏距离的远近匹配尾实体的话,会得到三个错误的答案,因为正确的尾实体按照欧氏距离计算的话会比较远,只有在比较 x 轴的距离时候,才能推断出正确的答案。文中说这种情况应该增大 y 轴 loss 的权重,减小 x 轴 loss 的权重,但我觉得反了,想了很久也没有想明白,可能按照之前模型的打分函数加负号的情况,就能说得通了。总之 point 就是给 embedding 的各个维度赋予不同的权重。
文章的核心贡献就是这个式子——打分函数: 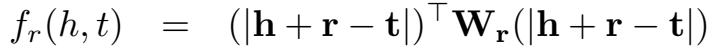
Loss:
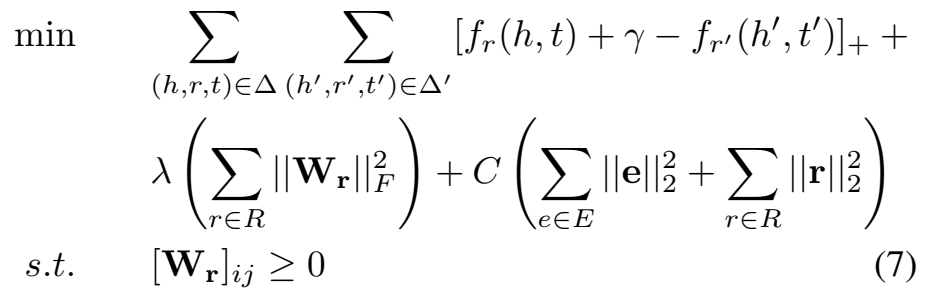
还有一点值得一提的是,为了减少参数量,达到与 TransE 相当的参数量,Wr 由基于三元组的 embedding 计算得出:
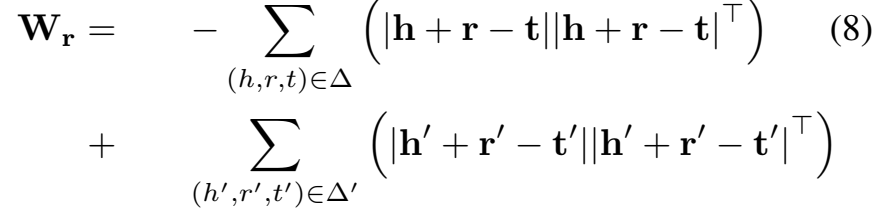
实验
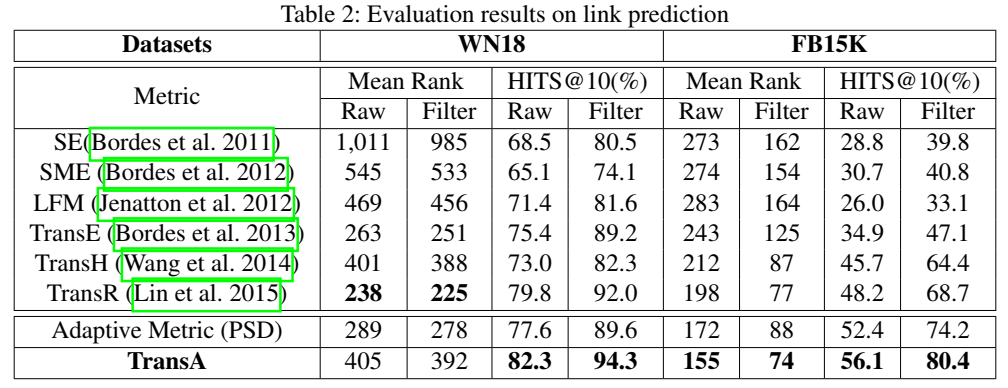
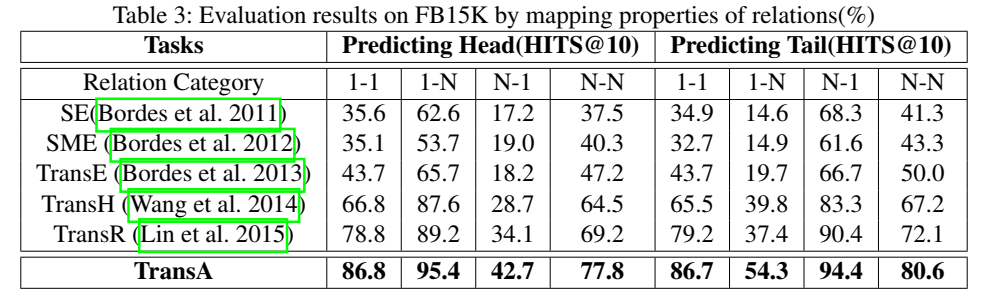
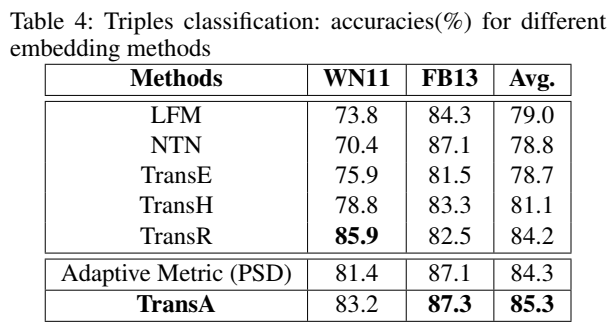
读完这篇论文,我的感觉就是:这是一篇靠写出来的论文,文章本身的创新点很小,但是居然能发到顶会上,可能有偶然和外在因素的影响,但就文章本身而言,需要学习的有如下几点:
(1)论文结构可以模仿。结构是中规中矩、简洁清晰的“引言-相关工作-方法-实验-结论”五段式结构。引言部分,针对自己方法,详细说明了传统欧氏距离方法的缺陷,令我脑海中冒出一句话:“世上本没有问题,造也要造出一个问题。”;相关工作将之前的工作分为“Translation-based”及其他两类,还是很严谨的;方法部分,因为对于指标做的小改进非常单薄,所以作者加上了“Perspective from Equipotential Surfaces”和“Perspective from Feature Weighting”两个角度的解释,使其看起来有理论支撑;实验部分,也是做了经典的链接预测和三元组分类两个实验,没有其他,但是在结果分析的时候分条解释的操作看起来很整齐;最后是结论。
(2)有一些比较“聪明”的表述值得学习。比如由示意图解释 TransA 可以处理“一对多”关系,因为 TransA 的指标是对称的,所以也可以处理“多对一”关系,又,因为“多对多”关系可以被视为多个“一对一”关系,因此推断 TransA 也可以处理“多对多”关系,实验也证明了这一点。再比如,对于 TransA 在 WN18 的 Mean Rank 没有达到最优,也给出了合理的解释,是因为测试集中某些个别的被排在最后的样本影响了整体的平均值。
虽然文章的贡献干货并不大,但是整体读起来很清爽很舒服,或许这就是能够被顶会录用的原因吧。
代码
TransA 的话,\(Pykg2vec\) 和 \(OpenKE\) 都没有实现,之前参考的一个大神实现的几个 KGE 模型上倒是有。
https://github.com/LYuhang/Trans-Implementation/blob/master/code/models/TransA.py
class TransA(nn.Module):
def __init__(self, entityNum, relationNum, embeddingDim, margin=1.0, L=2, lamb=0.01, C=0.2):
super(TransA, self).__init__()
assert (L==1 or L==2)
self.model = "TransE"
self.entnum = entityNum
self.relnum = relationNum
self.enbdim = embeddingDim
self.margin = margin
self.L = L
self.lamb = lamb
self.C = C
self.entityEmbedding = nn.Embedding(num_embeddings=entityNum,
embedding_dim=embeddingDim)
self.relationEmbedding = nn.Embedding(num_embeddings=relationNum,
embedding_dim=embeddingDim)
self.distfn = nn.PairwiseDistance(L)
'''
Normalize embedding
'''
def normalizeEmbedding(self):
pass
'''
Reset Wr to zero
'''
def resetWr(self, usegpu, index):
if usegpu:
self.Wr = torch.zeros((self.relnum, self.enbdim, self.enbdim)).cuda(index)
else:
self.Wr = torch.zeros((self.relnum, self.enbdim, self.enbdim))
def retEvalWeights(self):
return {"entityEmbed": self.entityEmbedding.weight.detach().cpu().numpy(),
"relationEmbed": self.relationEmbedding.weight.detach().cpu().numpy(),
"Wr": self.Wr.detach().cpu().numpy()}
'''
Calculate the Mahalanobis distance weights
'''
def calculateWr(self, posX, negX):
size = posX.size()[0]
posHead, posRel, posTail = torch.chunk(input=posX,
chunks=3,
dim=1)
negHead, negRel, negTail = torch.chunk(input=negX,
chunks=3,
dim=1)
posHeadM, posRelM, posTailM = self.entityEmbedding(posHead), \
self.relationEmbedding(posRel), \
self.entityEmbedding(posTail)
negHeadM, negRelM, negTailM = self.entityEmbedding(negHead), \
self.relationEmbedding(negRel), \
self.entityEmbedding(negTail)
errorPos = torch.abs(posHeadM + posRelM - posTailM)
errorNeg = torch.abs(negHeadM + negRelM - negTailM)
del posHeadM, posRelM, posTailM, negHeadM, negRelM, negTailM
self.Wr[posRel] += torch.sum(torch.matmul(errorNeg.permute((0, 2, 1)), errorNeg), dim=0) - \
torch.sum(torch.matmul(errorPos.permute((0, 2, 1)), errorPos), dim=0)
'''
This function is used to calculate score, steps follows:
Step1: Split input as head, relation and tail index array
Step2: Transform index array to embedding vector
Step3: Calculate Mahalanobis distance weights
Step4: Calculate distance as final score
'''
def scoreOp(self, inputTriples):
head, relation, tail = torch.chunk(input=inputTriples,
chunks=3,
dim=1)
relWr = self.Wr[relation]
head = torch.squeeze(self.entityEmbedding(head), dim=1)
relation = torch.squeeze(self.relationEmbedding(relation), dim=1)
tail = torch.squeeze(self.entityEmbedding(tail), dim=1)
# (B, E) -> (B, 1, E) * (B, E, E) * (B, E, 1) -> (B, 1, 1) -> (B, )
error = torch.unsqueeze(torch.abs(head+relation-tail), dim=1)
error = torch.matmul(torch.matmul(error, torch.unsqueeze(relWr, dim=0)), error.permute((0, 2, 1)))
return torch.squeeze(error)
def forward(self, posX, negX):
size = posX.size()[0]
self.calculateWr(posX, negX)
# Calculate score
posScore = self.scoreOp(posX)
negScore = self.scoreOp(negX)
# Calculate loss
marginLoss = 1 / size * torch.sum(F.relu(input=posScore-negScore+self.margin))
WrLoss = 1 / size * torch.norm(input=self.Wr, p=self.L)
weightLoss = ( 1 / self.entnum * torch.norm(input=self.entityEmbedding.weight, p=2) + \
1 / self.relnum * torch.norm(input=self.relationEmbedding.weight, p=2))
return marginLoss + self.lamb * WrLoss + self.C * weightLoss
TranSparse
paper: Knowledge Graph Completion with Adaptive Sparse Transfer Matrix
论文
这篇文章是自动化所赵军、刘康老师团队发表在 AAAI 2016 上的工作, 和 TransD 的作者是一个人。主要思想是:引入稀疏度解决知识库的异质性和不平衡性问题。TransD 和 TranSparse 都是从减少参数量出发的。
两个模型
知识图谱的异质性(heterogeneity)指某些关系与大量的实体连接,某些关系可能仅与少量实体连接;不平衡性(imbalance)指某些关系的头实体和尾实体的数量可能差别巨大。TranSparse(share)用于解决异质性问题,TranSparse(separate)用于解决不平衡性问题。
- TranSparse(share)
关系 r 的投影矩阵 \(M_r\) 的稀疏度定义为:

\(N_r\) 指关系 r 连接的实体对的数量,如果越多,则投影矩阵的稀疏度越小,矩阵越密集(即非 0 元素个数越多)。\(N_r\) 表示连接实体对数最多的值。
投影操作:
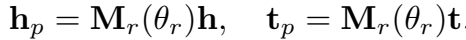
这里,头尾实体共享一个投影矩阵。
- TranSparse(separate)
在这种模式下,头尾实体使用不同的投影矩阵,两个投影矩阵的稀疏度由下式决定:
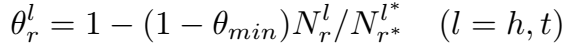
其中,\(N_r^l\) 表示 “the number of entities linked by relation r at location l ”(不是很明白=.=),带 * 表示最大值。
投影操作:
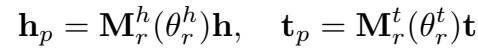
TranSparse(share, separate) 的三元组评分函数都是: 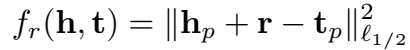
Loss: 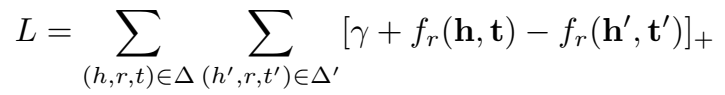
据原文表述,TranSparse 的时间和空间复杂度与 TransH、TransD 相当。
实验
文章进行了三元组分类和链接预测实验。
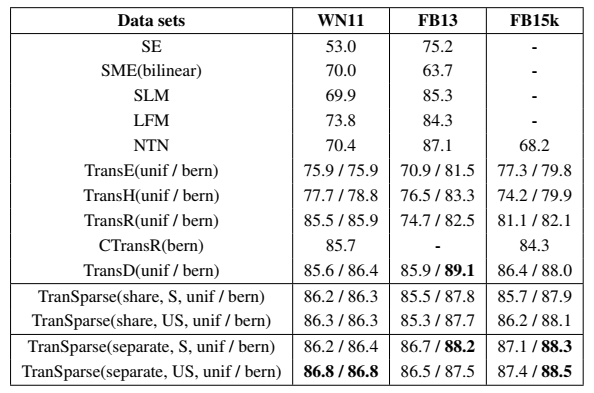
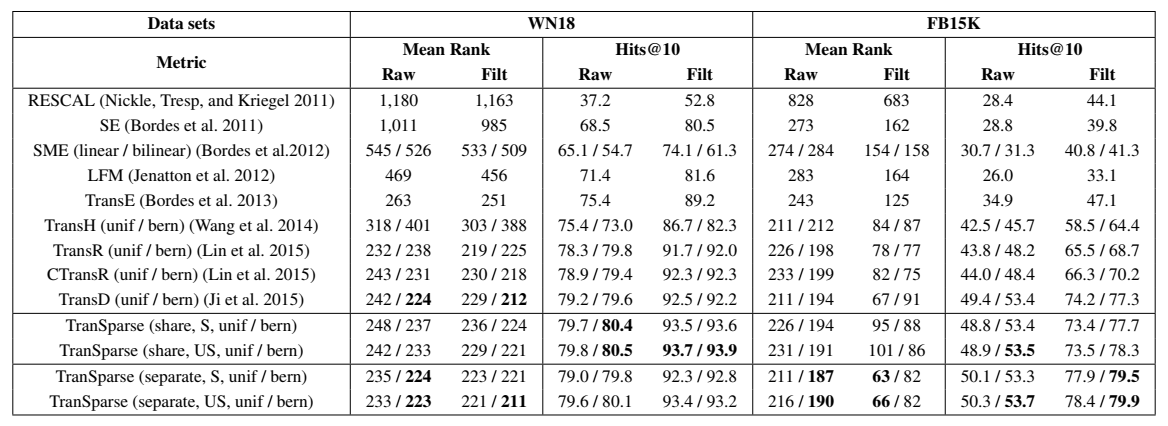
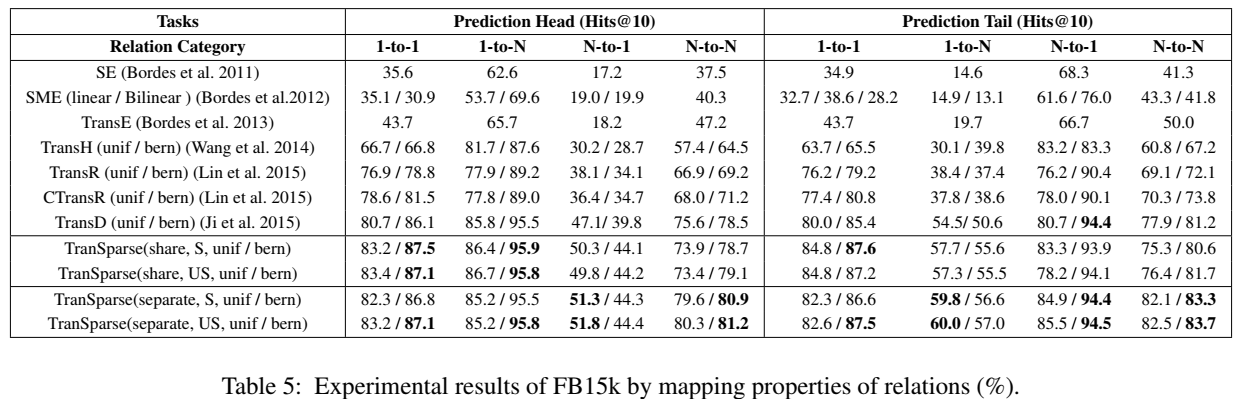
实验中对比的 baseline 并不多,TranSparse 自己的模型就占了四行,很多论文是这样,自己提出的模型有很多个小 trick,可以视为几个子模型,与 baseline 一齐比较,即使其中任意一个达到 state-of-the-art 的效果,都是成功,看起来会比较好看,在 baseline 比较少的情况下不会使实验部分看起来很单薄。
代码
\(Pykg2vec\) 和 \(OpenKE\) 都没有实现 TranSparse,github 上也没有找到 PyTorch 版本的实现,只有一个 Tensorflow 版本的,因为对 TensorFlow 不太熟悉,所以没有细读代码,传送门放在这里,备需:https://github.com/FrankWork/transparse/blob/master/transparse/transparse_model.py
最近看论文比较能看进去了,看的这几篇经典老论文,发觉比较 easy 了,有如下几个原因吧:一是因为 TransE 后面的这些模型都是中国人提出来的,看这些人写的英文可能相对容易一些;二是自己能静下心来了,这是很重要的一个原因吧,不怕慢,只是去做;还有一个原因就是,自己写过一篇文章,再去看,会有一些些代入感,可能会有几分站在作者的角度去思考了,会关注作者怎样构建这篇文章,关注他/她想要表达什么意思。这很好,只要心静下来,就能走得很远很远。


