UM (Unstructured Model) 和 SE (Structured Embedding)
这两篇论文可以算是 TransE 的前身,也都是 TransE 的作者 Antoine Bordes 提出来的,觉得有必要看一下。
UM (Unstructured Model)
paper: Joint Learning of Words and Meaning Representations for Open-Text Semantic Parsing
概述
文章作者是 Antoine Bordes,发表于 2012 年的 AISTATS (CCF-C)。这篇文章并没有提到 Knowledge Graph 的概念,但是也是对三元组进行训练。文章的卖点是将词和三元组中的实体一起进行训练,语义解析(semantic parsing)在这里就是从非结构化文本中抽取三元组并进行实体消歧。王泉老师 和 Dat Quoc Nguyen 的综述中将其称为 Unstructured Model,并且打分函数是 \(-\lVert h-t\rVert_2^2\),所以业界就这么传开了,但我看了这篇论文,根本不是这么回事啊,不知是综述里引用错了论文,这根本不是 UM,还是怎么回事。

首先使用工具从非结构化文本中提取三元组,然后进行实体消歧,即计算出三元组中的头尾实体和关系对应于 WordNet 同义词集中的哪个语义。文章的核心贡献在于能量函数的定义,该语义匹配能量函数被用于预测给定词元(lemma)的合适的同义词集(synsets)(即语义)。
能量函数
这个能量函数的设计还是有点东西的,根本不是\(-\lVert h-t\rVert_2^2\) 这么 naive。

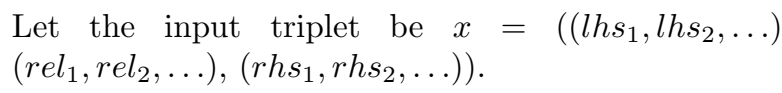
输入三元组的头尾实体和关系是包含多个语义的,会有一个 pooling 操作 \(\pi\) 对多个语义进行一下融合:

然后如图所示,对 \(E_{lhs}\) 和 \(E_{rhs}\) 过一个 \(g(\cdot)\) 函数,右侧同理,即
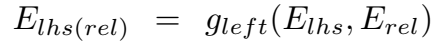
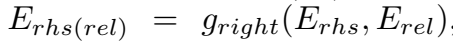
然后对上面两者的结果过 \(h(\cdot)\) 函数,得到能量函数 \(\varepsilon\):
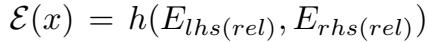
在论文中,\(g(\cdot)\) 被设计为双线性层(bilinear layer),\(h(\cdot)\) 设计为点积(\(\bigotimes\) 是向量积):
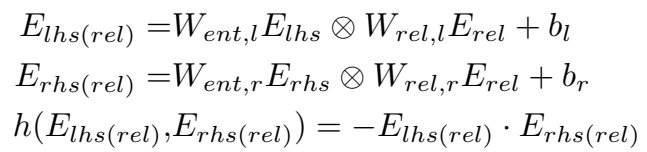
训练
训练目标和训练过程与 Trans 系列模型都一样,对训练样本负采样,使正样本的能量函数值尽可能低,负样本的尽可能高,也加了一些归一化的约束,使用 SGD 进行优化。
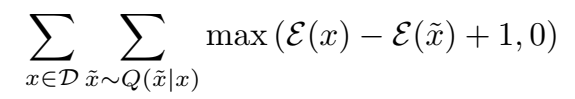
SE (Structured Embedding)
paper: Learning Structured Embeddings of Knowledge Bases
概述
文章发表于 AAAI 2011,比上文还早一年,所以我严重怀疑上文不是 UM,文章作者还是 Antoine Bordes。文章明确指出这是一个用于学习 KGE 的方法,并称为是一个基于神经网络的方法,其实,神经网络的本质就是矩阵计算,从这个意义上说,所有的 Trans 系列模型都可以视为基于浅层神经网络的。文章从 WordNet 和 Freebase 自制了数据集进行实验。
三元组打分函数
给定关系 \(k\),其头尾实体的相似性度量如下,\(R_k^{lhs}\) 和 \(R_k^{rhs}\) 分别为关系 \(k\) 对应的两个矩阵。
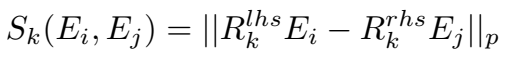
三元组打分函数其实跟上面是一样的,\(E\) 是实体映射矩阵,函数 \(v(\cdot)\) 将实体索引号映射为 one-hot 向量。函数使用 L1 范数。
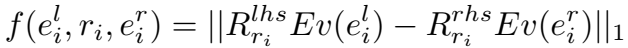
核密度估计
这部分称为 Probability Landscape Estimation,提出了一种更高级的打分函数,说是为了 estimate the probability density at any point of the defined embedding space using Kernel Density Estimation (KDE) (说实话我没看明白它为什么要这么干=.=||),就暂且理解为一种带有确定性(certainty)的三元组打分函数吧。
对于一个三元组对 \((x_i,x_j)\),其相似性度量为下面这样的高斯核:
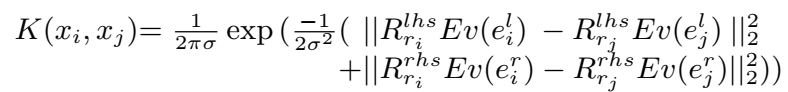
核的密度估计,即三元组 \(x_i\) 的得分为:
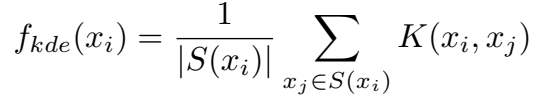
其中,
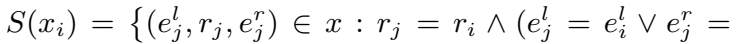
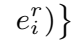
预测实体为 KDE 得分最高的实体:
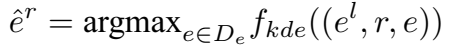
实验
在两个数据集上进行链接预测实验:
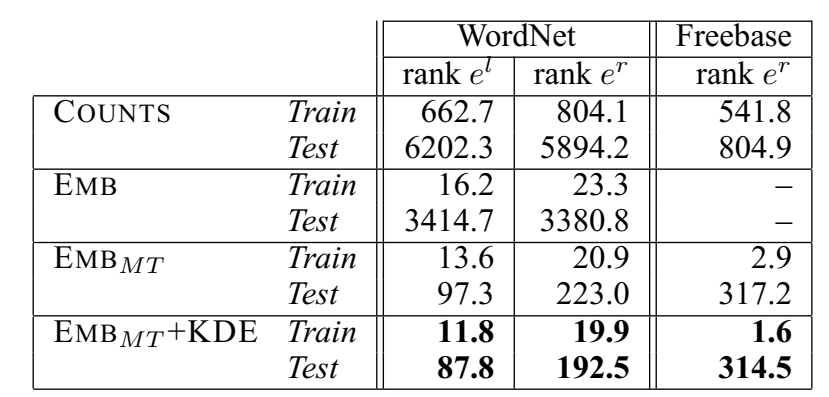
Mean Rank 结果:
Hits@10 结果:
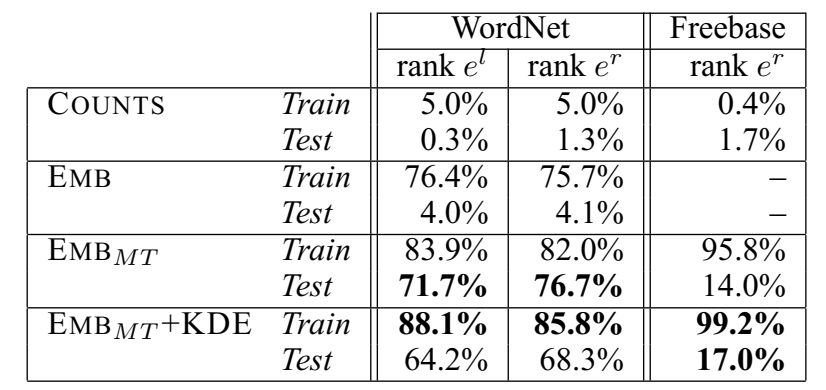
- \(COUNTS\):不训练,只计数共现对的统计结果
- \(EMB\):使用普通的三元组打分函数,但是头尾实体用两份映射表
- \(EMB_{MT}\):使用普通的三元组打分函数,头尾实体用一份映射表
- \(EMB_{MT} + KDE\):使用 KDE 打分函数
实验证明,\(EMB_{MT} + KDE\) 的效果最好。
这两篇论文在飞速发展的 AI 领域,已经算是远古的模型了,估计也不会有人去复现,所以没有找代码。



