KMP算法是一种优秀的字符串匹配算法,字符串匹配的常规算法是一步一步进行移位和比较操作,直至找到完全相匹配的字符串。
下面通过一个例子,为大家仔细说明KMP算法的使用和思路:
问题:
在字符串“DEABCDABABCDABCDABDE”字符串中,匹配字符串"ABCDABD".
算法思路:
KMP算法的思路在于,根据已经匹配的部分字符的信息,不把搜索位置移回已经比较过的位置,这样就提高了效率,是不是还是有点不清楚?没关系,让我们来根据一个例子来切实体会一下KMP算法是如何实现的。
图解:
1、KMP算法的核心是一张“部分匹配表”,这个表是怎么来的,后面再说,先用了再说,下图就是该问题的部分匹配表。

这个表上面一行是我们的模式字符串,下面一行是每个字符所对应的匹配值
移位规则是 移动位数 = 已匹配的字符串长度 - 已匹配字符串的最后一位字符所对应的匹配值。
2、接下来就开始进行操作
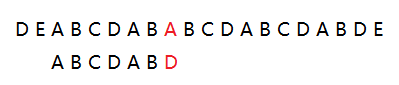
上图中我们看到,移位两位后,我们找到了部分匹配的字符串"ABCDAB",但并没有找到完全匹配的字符串,如果是常规思路,就是在继续往下一步一步移位,但我们这里不这样进行,我们观察到,已经匹配的字符串长度是6,匹配到的最后一个字符是"B",查询部分匹配表,这个“B”的部分匹配值是2,那么根据我们算法的移位规则,下一步我们的移位长度 = 6 - 2 = 4;
3、

╮(╯▽╰)╭,有没有发现,移了4位之后,刚好到达了下一个“AB”处?是不是很神奇?好了,打住,我们继续往下移,当前已匹配的字符串长度为2,查询这个“B”的匹配值为0(别和上个B搞混了),根据算法,我们接下来移位长度是 2 - 0 = 2;
4、

继续,和前面的步骤相同,我们这次移位长度为 6 - 2 = 4;
5、
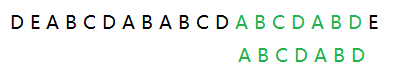
至此,我们已经找到了完全匹配的字符串,当然,如果母字符串的长度较长,我们可以继续进行移位,继续寻找,和之前的步骤相同,下次我们移位长度为 7 - 0 = 7。
算法分析:
不知道大家看到现在,有没有一点明悟?来,让我们分析一下模式字符串“ABCDABD”:
对于搜索来说,我们首先关注的肯定是第一个字符,如果第一个字符都不匹配,那么后面的字符就没有比较的必要了,该目标字符串的第一个字符是’A‘,让我们看看这个字符串里有没有’A‘,诶,还真有,假如说我们现在已经匹配了“ABCDA”,5个字符,我们要移4位才能从第一个'A'移到第二个'A',’A‘只有一个字符,5 - 1 = 4;
再往下看,关注完第一个字符,我们开始关注和第一个字符依次相连的子字符串,这些字符串有一个共性,就是第一个字符都是’A‘,那我们看看这种字符串能有多少,"AB","ABC","ABCD","ABCDA","ABCDAB","ABCDABD",再看看这些字符串在目标字符串“ABCDABD”中存在几个,可以看出,除去和第一个“A”相连的,“AB”还有一个,其余的没有,而"AB"长度为2,所以在表中,第二个B的匹配值为2。
该算法的核心思路在于,有时候,字符串的头部和尾部可能会有重复。
不知道大家有没有听懂?让我们把匹配字符串换一下,换成“ABCDABC”,现在的部分匹配表应该是:

算法思考和延伸:
如果模式字符串过长,部分匹配表的生成会占用较多的时间,如何去提高部分匹配表的生成效率,是该算法的优化所在。(个人观点,如有大佬,请指教!)
该算法思想和字典编码有一定的相通之处。改天我会写出一个字典编码的文章。敬请期待!



