算法+OpenCV】基于opencv的直线和曲线拟合与绘制（最小二乘法）

最小二乘法多项式曲线拟合，是常见的曲线拟合方法，有着广泛的应用，这里在借鉴最小二乘多项式曲线拟合原理与实现的原理的基础上，介绍如何在OpenCV来实现基于最小二乘的多项式曲线拟合。

概念

最小二乘法多项式曲线拟合，根据给定的m个点,并不要求这条曲线精确地经过这些点，而是曲线y=f(x)的近似曲线y= φ(x)。

 

原理

给定数据点pi(xi,yi)，其中i=1,2,…,m。求近似曲线y= φ(x)。并且使得近似曲线与y=f(x)的偏差最小。近似曲线在点pi处的偏差δi= φ(xi)-y，i=1,2,...,m。

 

常见的曲线拟合方法:

1.使偏差绝对值之和最小

 

2.使偏差绝对值最大的最小

 

3.使偏差平方和最小

 

 

按偏差平方和最小的原则选取拟合曲线，并且采取二项式方程为拟合曲线的方法,称为最小二乘法。

 

推导过程：

1. 设拟合多项式为：

2.各点到这条曲线的距离之和，即偏差平方和如下：

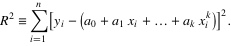
3.为了求得符合条件的a值，对等式右边求ai偏导数，因而我们得到了：

.......

 

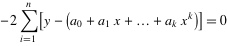
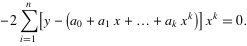
4.将等式左边进行一下化简，然后应该可以得到下面的等式：

.......

 

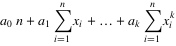
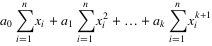
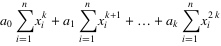
5.把这些等式表示成矩阵的形式，就可以得到下面的矩阵：

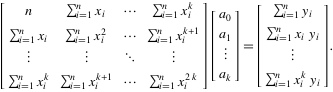
6.即X*A=Y。

 

我们只要解出这个线性方程，即可求得拟合曲线多项式的系数矩阵。而在opencv中，有一个专门用于求解线性方程的函数，即cv::solve()，具体调用形式如下：

 

int cv::solve(
cv::InputArray X, // 左边矩阵X, nxn
cv::InputArray Y, // 右边矩阵Y,nx1
cv::OutputArray A, // 结果，系数矩阵A,nx1
int method = cv::DECOMP_LU // 估算方法
);

int cv::solve(
	cv::InputArray X, // 左边矩阵X, nxn
	cv::InputArray Y, // 右边矩阵Y,nx1
	cv::OutputArray A, // 结果，系数矩阵A,nx1
	int method = cv::DECOMP_LU // 估算方法
);

 

 

我们只需要按照上述原理，构造出矩阵X和Y，即可调用该函数，计算出多项式的系数矩阵A。

opencv中支持的估算方法如下图所示：

 

实现如下：

 

bool polynomial_curve_fit(std::vector<cv::Point>& key_point, int n, cv::Mat& A)
{
//Number of key points
int N = key_point.size();

//构造矩阵X
cv::Mat X = cv::Mat::zeros(n + 1, n + 1, CV_64FC1);
for (int i = 0; i < n + 1; i++)
{
for (int j = 0; j < n + 1; j++)
{
for (int k = 0; k < N; k++)
{
X.at<double>(i, j) = X.at<double>(i, j) +
std::pow(key_point[k].x, i + j);
}
}
}

//构造矩阵Y
cv::Mat Y = cv::Mat::zeros(n + 1, 1, CV_64FC1);
for (int i = 0; i < n + 1; i++)
{
for (int k = 0; k < N; k++)
{
Y.at<double>(i, 0) = Y.at<double>(i, 0) +
std::pow(key_point[k].x, i) * key_point[k].y;
}
}

A = cv::Mat::zeros(n + 1, 1, CV_64FC1);
//求解矩阵A
cv::solve(X, Y, A, cv::DECOMP_LU);
return true;
}

bool polynomial_curve_fit(std::vector<cv::Point>& key_point, int n, cv::Mat& A)
{
	//Number of key points
	int N = key_point.size();

	//构造矩阵X
	cv::Mat X = cv::Mat::zeros(n + 1, n + 1, CV_64FC1);
	for (int i = 0; i < n + 1; i++)
	{
		for (int j = 0; j < n + 1; j++)
		{
			for (int k = 0; k < N; k++)
			{
				X.at<double>(i, j) = X.at<double>(i, j) +
					std::pow(key_point[k].x, i + j);
			}
		}
	}

	//构造矩阵Y
	cv::Mat Y = cv::Mat::zeros(n + 1, 1, CV_64FC1);
	for (int i = 0; i < n + 1; i++)
	{
		for (int k = 0; k < N; k++)
		{
			Y.at<double>(i, 0) = Y.at<double>(i, 0) +
				std::pow(key_point[k].x, i) * key_point[k].y;
		}
	}

	A = cv::Mat::zeros(n + 1, 1, CV_64FC1);
	//求解矩阵A
	cv::solve(X, Y, A, cv::DECOMP_LU);
	return true;
}

 

测试代码如下：

 

int main()
{
//创建用于绘制的深蓝色背景图像
cv::Mat image = cv::Mat::zeros(480, 640, CV_8UC3);
image.setTo(cv::Scalar(100, 0, 0));

//输入拟合点
std::vector<cv::Point> points;
points.push_back(cv::Point(100., 58.));
points.push_back(cv::Point(150., 70.));
points.push_back(cv::Point(200., 90.));
points.push_back(cv::Point(252., 140.));
points.push_back(cv::Point(300., 220.));
points.push_back(cv::Point(350., 400.));

//将拟合点绘制到空白图上
for (int i = 0; i < points.size(); i++)
{
cv::circle(image, points[i], 5, cv::Scalar(0, 0, 255), 2, 8, 0);
}

//绘制折线
cv::polylines(image, points, false, cv::Scalar(0, 255, 0), 1, 8, 0);

cv::Mat A;

polynomial_curve_fit(points, 3, A);
std::cout << "A = " << A << std::endl;

std::vector<cv::Point> points_fitted;

for (int x = 0; x < 400; x++)
{
double y = A.at<double>(0, 0) + A.at<double>(1, 0) * x +
A.at<double>(2, 0)*std::pow(x, 2) + A.at<double>(3, 0)*std::pow(x, 3);

points_fitted.push_back(cv::Point(x, y));
}
cv::polylines(image, points_fitted, false, cv::Scalar(0, 255, 255), 1, 8, 0);

cv::imshow("image", image);

cv::waitKey(0);
return 0;
}

int main()
{
	//创建用于绘制的深蓝色背景图像
	cv::Mat image = cv::Mat::zeros(480, 640, CV_8UC3);
	image.setTo(cv::Scalar(100, 0, 0));

	//输入拟合点  
	std::vector<cv::Point> points;
	points.push_back(cv::Point(100., 58.));
	points.push_back(cv::Point(150., 70.));
	points.push_back(cv::Point(200., 90.));
	points.push_back(cv::Point(252., 140.));
	points.push_back(cv::Point(300., 220.));
	points.push_back(cv::Point(350., 400.));

	//将拟合点绘制到空白图上  
	for (int i = 0; i < points.size(); i++)
	{
		cv::circle(image, points[i], 5, cv::Scalar(0, 0, 255), 2, 8, 0);
	}

	//绘制折线
	cv::polylines(image, points, false, cv::Scalar(0, 255, 0), 1, 8, 0);

	cv::Mat A;

	polynomial_curve_fit(points, 3, A);
	std::cout << "A = " << A << std::endl;

	std::vector<cv::Point> points_fitted;

	for (int x = 0; x < 400; x++)
	{
		double y = A.at<double>(0, 0) + A.at<double>(1, 0) * x +
			A.at<double>(2, 0)*std::pow(x, 2) + A.at<double>(3, 0)*std::pow(x, 3);

		points_fitted.push_back(cv::Point(x, y));
	}
	cv::polylines(image, points_fitted, false, cv::Scalar(0, 255, 255), 1, 8, 0);

	cv::imshow("image", image);

	cv::waitKey(0);
	return 0;
}

绘制结果：