一文详解分析鱼眼相机投影成像模型和畸变模型
1.为什么要设计鱼眼镜头?
鱼眼镜头设计的目的是要拍摄大的视野,鱼眼镜头的视场角可达到180-270度,在工程上视角超过140度的镜头被统称为鱼眼镜头。这是因为普通针孔相机视野太小,满足不了一些特别的需求。
为什么针孔相机达不到这么大的视场角呢?因为针孔相机模型是相似性投影,实际场景中的直线仍被投影成图像面上的直线。假如使用针孔相机模型达到180度的视场角,那么这种情况下的图像会变为无穷大。
那么怎么设计才能达到这种大视场角的效果?
为了将尽可能大的场景投影到有限的图像平面内,鱼眼相机将相机畸变列为其成像特征用以在有限的图像平面内表达本应落在无穷远处的空间点投影。
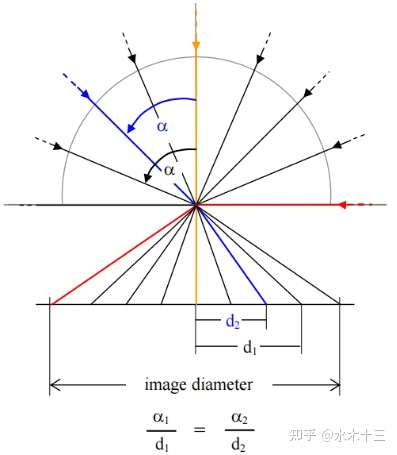
鱼眼镜头设计采用非相似性成像,在成像过程中引入畸变,引入畸变的作用是通过对直径空间的压缩,突破成像视角的局限,从而达到广角成像。
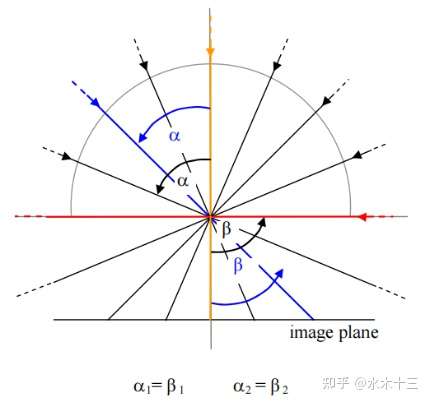
鱼眼镜头是为了大视野,自动放弃了相似性成像,选择非相似性成像。因此经入射光线经过镜头之后射向成像面,其出射角一定是要小于入射角的。
 fisheye projection model
fisheye projection model因此设计出了鱼眼镜头。
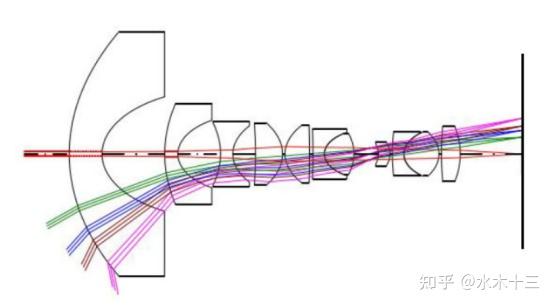
鱼眼镜头是由十几个不同的透镜组合而成的,在成像过程中,入射光线经过不同程度的折射,投影到尺寸有限的成像平面上,使得鱼眼镜头与普通镜头相比拥有更大的视野。
结构中前面的类似凸的镜头发生折射,使入射角减小,其余镜头相当于一个成像镜头。
2.鱼眼相机成像模型?
鱼眼相机成像模型近似为单位球面投影模型。
一般将鱼眼相机成像过程分解成两步:先将三维空间点线性的投影到虚拟单位球面上;随后将单位球面上的点投影到图像平面上,这个过程是非线性的。
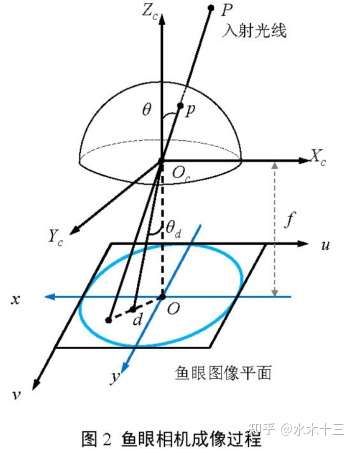
鱼眼相机的设计引入了畸变,因此鱼眼相机所成影像存在畸变,其中径向畸变非常严重,因此其畸变模型主要考虑径向畸变。
鱼眼相机的投影函数是为了尽可能将庞大的场景投影到有限的图像平面所设计的。根据投影函数的不同将鱼眼相机的设计模型大致分为等距投影模型、等立体角投影模型、正交投影模型和体视投影模型四种。相机的成像模型实际上表征的是成像的像高与入射角之间的映射关系。
那么鱼眼相机模型是如何将空间中的一点P投影到球面上,进而投影到图像平面上的。
2.1 针孔投影模型
针孔投影模型为相似性投影模型,其满足物点、成像中心、像点的共线关系,其理想成像公式为:
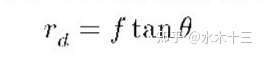
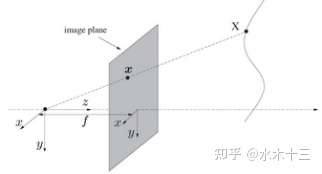
2.2 等距投影模型
等距投影模型的投影关系在入射光线之间的角度相同时,保持其对应各投影点之间的间距相同。其投影模型为:
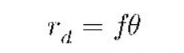
rd表示图像中点到畸变中心的距离,即成像高度;f为鱼眼相机的焦距,θ是入射光线与鱼眼相机光轴之间的夹角,即入射角。
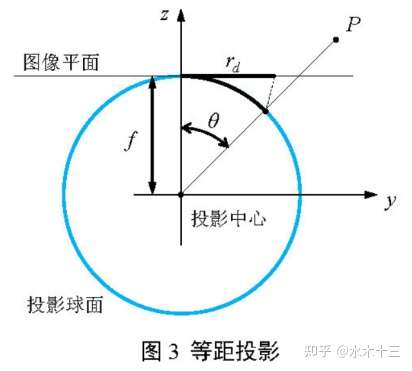
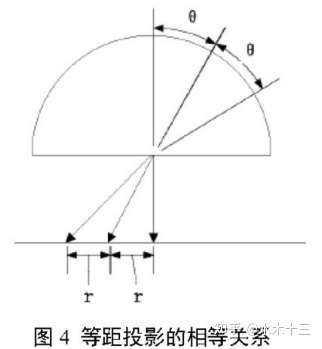
2.3 等立体角投影模型
等立体角的特点是相等立体角的入射面会产生相等面积的像,其畸变程度介于等距模型与正交模型之间。其模型如下:
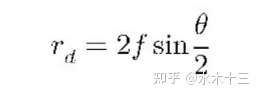
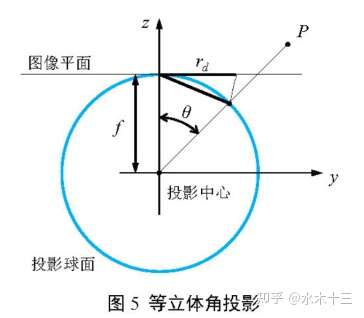
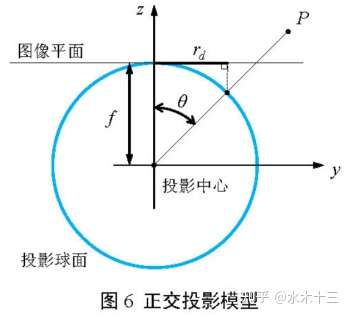
2.4 正交投影模型
正交投影模型的畸变很大,近180度处的图像信息几乎全部丢失,且180度之外的场景区域将无法进行描述。采用这种模型的镜头拍出的图片即使在视角较小的区域也会比其他模型镜头的畸变更明显。因此,针对艺术摄影类的广角镜头,该模型的校正效果更好。其模型如下:
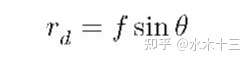
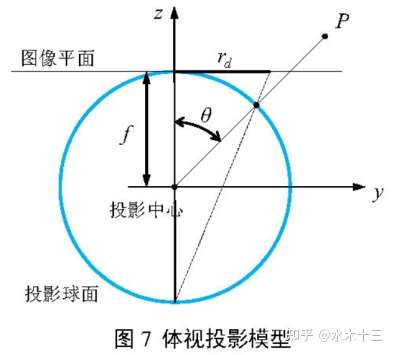
2.5 体视投影模型
体视模型相比之下畸变最小,球形物面上的微小面元经过体视投影后,其像仍然是一个小圆。所以体视投影对微小物体成像有相似性。但正是这种成像的相似性,使得该投影方式不能提供足够的桶形畸变,影响成像视场。其模型如下:
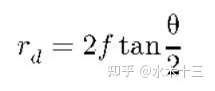
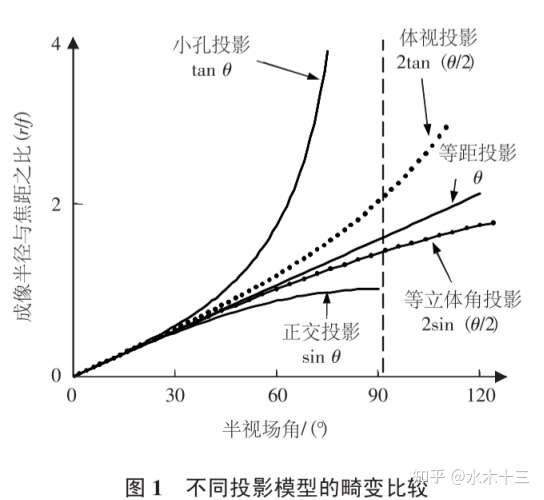
2.6 几种投影模型的区别
四种畸变模型畸变量从大到小依次为:正交投影、等立体角投影、等距投影、体视投影。由于等距投影模型便于计算,因此被各大工程广泛应用。
3. 通用鱼眼相机模型-Kannala-Brandt 模型
鱼眼镜头生产过程中不可能精确地按照投影模型来设计,所以为了方便鱼眼相机的标定,Kannala-Brandt提出了一种鱼眼相机的一般多项式近似模型。通过前面四个模型,可以发现θd是theta的奇函数,将这些式子按泰勒级数展开,发现θd用θ的奇次多项式表示,即
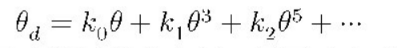
取前5项,给出了足够的自由度来很好的近似各种投影模型。
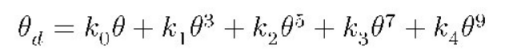
上式是根据四种鱼眼相机投影模型得出的一种通用鱼眼相机多项式模型。
这种模型可以通过θ得到θd,通过无畸变图像中的点能够计算出鱼眼图像中的畸变点。
OpenCV中鱼眼相机标定方法就是用的这种KB模型。
4. 空间点到图像的投影过程
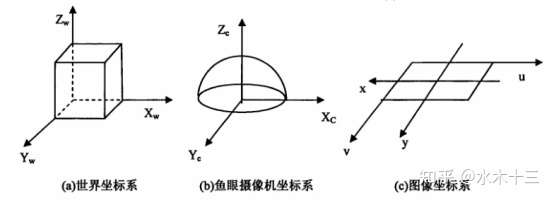

Step1. 世界坐标系转相机坐标系Camera
相机坐标系下的一点P(Xc,Yc,Zc)。
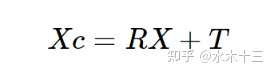
Step2. camera转归一化相机球面上
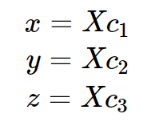
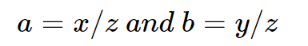
Step3. 计算θ角
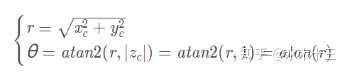
由直角三角形正切公式推出。
其中r为景物通过鱼眼相机投影在传感器上的像高,即图像中像素点到主点的距离。
Step4. 利用KB畸变模型进行加畸变处理
因为镜头设计有误差,θ-->θd。
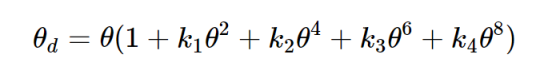
Step5. 计算该点在图像物理坐标系中的坐标
根据等距投影模型,d=fθd,f=1,由三角形相似,d/r=x’/a 推导出以下公式:
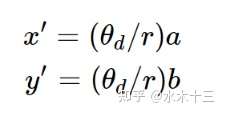
Step6. 最终图像像素坐标系uv
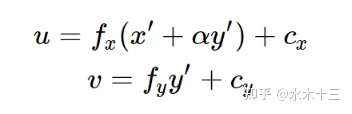
这一步α是扭曲系数,fx,fy,cx,cy是鱼眼镜头的内参矩阵,作用是两个二维平面间的缩放和平移。缩放是要把物理单位转成像素单位,平移是坐标原点对齐。
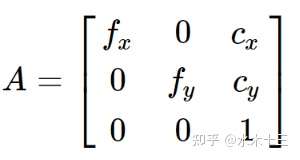





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构
· 提示词工程——AI应用必不可少的技术
· 字符编码:从基础到乱码解决
· 地球OL攻略 —— 某应届生求职总结