UVA 11174 Stand in a Line

　　题目大意：有n个人构成森林关系。现在要把他们排成一列，使儿子不在父亲前面，求方案数。n<=40000。

　　惊叹数学之妙。

　　首先看见森林，不如来一个超级点做根。

　　设f[i]表示处理完i与i的子树的方案数，size[i]表示子树大小，j是i的儿子。

　　首先对于两棵子树，它们之间是互不影响的，所以方案数应该相乘，这部分表示出来就是：

　　　　

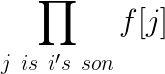
　　然后思考对于一种对于每个j的内部顺序已经确定，求i有多少种放法？这就相当于一个可重集合的模型(在j内的相当于一个重复元素)：

　　

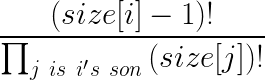
　　然后两部分用乘法原理乘起来，就是f[i]：

　　

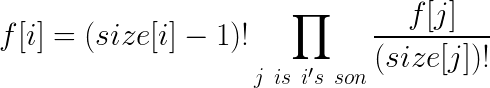
　　这个就可以写这道题了。

　　但实际上可以进一步化简？我们来考虑把一个f[j]拆开。设j的儿子是x：

　　

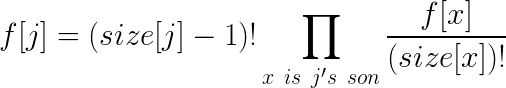
　　然后f[i]的式子里的size[j]!可以被(size[j]-1)!消成size[j]。

　　思维发散一下，f[i]内的size!和(size-1)!都会被消成1/size。

　　最后的答案是f[0]：

　　

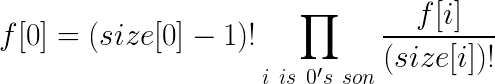
　　因为(size[0]-1)!=n!，最后答案就是：

　　

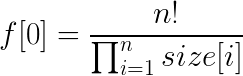
#include    <iostream>
#include    <cstdio>
#include    <cstdlib>
#include    <algorithm>
#include    <vector>
#include    <cstring>
#include    <queue>
#include    <complex>
#include    <stack>
#define LL long long int
#define dob double
#define FILE "11174"
using namespace std;

const int N = 40010;
const int Mod = 1000000007;
struct Node{int to,next;}E[N];
int n,m,head[N],tot;
int J[N],Ny[N],size[N],fa[N];

inline int gi(){
  int x=0,res=1;char ch=getchar();
  while(ch>'9'||ch<'0'){if(ch=='-')res*=-1;ch=getchar();}
  while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
  return x*res;
}

inline void link(int u,int v){
  E[++tot]=(Node){v,head[u]};
  head[u]=tot;
}

inline void pre(){
  Ny[1]=J[1]=1;
  for(int i=2;i<N;++i){
    J[i]=1ll*J[i-1]*i%Mod;
    Ny[i]=1ll*(Mod-Mod/i)*Ny[Mod%i]%Mod;
  }
}

inline void dfs(int x){
  size[x]=1;
  for(int e=head[x];e;e=E[e].next)
    dfs(E[e].to),size[x]+=size[E[e].to];
}

inline void solve(int Ans=0){
  memset(fa,0,sizeof(fa));
  memset(head,0,sizeof(head));
  n=gi();m=gi();tot=0;
  for(int i=1;i<=m;++i)fa[gi()]=gi();
  for(int i=1;i<=n;++i)link(fa[i],i);
  dfs(0);Ans=J[n];
  for(int i=1;i<=n;++i)Ans=1ll*Ans*Ny[size[i]]%Mod;
  printf("%d\n",(Ans+Mod)%Mod);
}

int main()
{
  freopen(FILE".in","r",stdin);
  freopen(FILE".out","w",stdout);
  pre();int Case=gi();while(Case--)solve();
  fclose(stdin);fclose(stdout);
  return 0;
}