UVA 11600 Masud Rana

　　题目大意：有一个n个点的完全图，有些路上有妖怪。现在一个人从一号点出发，每天随机走向另一个点，消灭路上的妖怪，问平均几天后所有点之间存在没有妖怪的路径。点数≤30。

　　看到点这么少肯定状压，看见存不下肯定map，事实上这题数据不够强力，很多复杂度不对的东西都可以艹过去(比如我的算法)。

　　首先可以缩点，把本来存在路径的点缩起来。

　　设f(x)表示：当安全的点集为x时，处理完所有的点的期望次数。

　　那么可以写出一个解不出来的式子：

　　

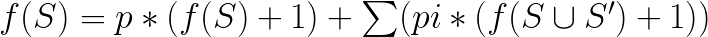
　　p表示走到自己集合内的概率，pi表示走到另一个点的概率。

　　解不出来是因为存在自己更新自己。怎么办呢？正常人都会想着化式子吧。

 

　　

　　

　　

　　

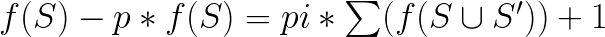
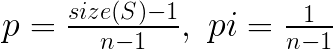
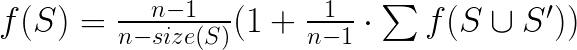
　　发现每次处理，集合都会变大。

　　这个时候打一个记忆搜就可以了。边界状态是f[2^n-1]=0.00。

#include    <iostream>
#include    <cstdio>
#include    <cstdlib>
#include    <algorithm>
#include    <map>
#include    <cstring>
#include    <queue>
#include    <complex>
#include    <stack>
#define LL long long int
#define dob double
#define FILE "11600"
using namespace std;

const int N = 110;
map<int,double>Mp;
int n,m,fa[N],bin[N],U[N];

inline int gi(){
  int x=0,res=1;char ch=getchar();
  while(ch>'9'||ch<'0'){if(ch=='-')res*=-1;ch=getchar();}
  while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
  return x*res;
}

inline int find(int x){
  return x==fa[x]?x:fa[x]=find(fa[x]);
}

inline double dfs(int S){
  if(Mp.find(S)!=Mp.end())return Mp[S];
  double Ans=0.0,sz=0.0;
  for(int i=1;i<=n;++i){
    if(S&bin[i-1]){sz+=1.0;continue;}
    Ans+=dfs(S|U[i]);
  }
  Ans=(1.0*n-1.0)/(1.0*n-sz)*(Ans/(1.0*n-1.0)+1.0);
  return Mp[S]=Ans;
}

inline void solve(){
  Mp.clear();bin[0]=1;
  n=gi();m=gi();if(n==1){puts("0");return;}
  for(int i=1;i<=n;++i)fa[i]=i,bin[i]=bin[i-1]<<1,U[i]=bin[i-1];
  for(int i=1;i<=m;++i){
    int f1=find(gi()),f2=find(gi());
    if(f1!=f2)fa[f2]=f1,U[f1]|=U[f2];
  }
  for(int i=1;i<=n;++i)U[i]=U[find(i)];
  Mp[bin[n]-1]=0.0;printf("%.10lf\n",dfs(U[1]));
}

int main(){
  freopen(FILE".in","r",stdin);
  freopen(FILE".out","w",stdout);
  int Case=gi();
  for(int t=1;t<=Case;++t)
    printf("Case %d: ",t),solve();
  fclose(stdin);fclose(stdout);
  return 0;
}