UVALive 3716 DNA Regions

题目大意：给定两个长度相等的字符串A和B，与一个百分比p%，求最长的、失配不超过p%的区间长度。O(nlogn)。

题目比较简单套路，推推式子就好了。

记S[i]表示到下标i一共有多少个失配，就相当于前缀和。那么对于一段区间[l,r]，有以下式子成立：

然后转化一下得到：

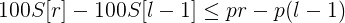
把变量相同的项放在一边：

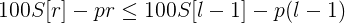
两边形式是一样的，不妨设：

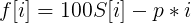
则有：

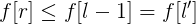
枚举右端点r，找到左边最左边的、f值大于等于它的值，即为对于r的答案。

怎么找呢？一种方法是按f值sort一下，把下标扔进堆里，或者随便搞搞就可以了。

还有一种方法是记录前缀最大值，二分查找即可，复杂度O(nlogn)，可以过去。

还有一种复杂度相同，但常数更小的方法：

看上面那个前缀最大值，答案一定在出现变化的点上。

我们把变化的点记录下来，在这上面二分就好了。

因为数组长度会变小，所以可以大力降常。

#include    <iostream>
#include    <cstdio>
#include    <cstdlib>
#include    <algorithm>
#include    <vector>
#include    <cstring>
#include    <queue>
#include    <complex>
#include    <stack>
#define LL long long int
#define dob double
#define FILE "3716"
using namespace std;

const int N = 150010;
int n,p,S[N],f[N],bin[N],tot,Mx,Ans;
char A[N],B[N];

inline int gi(){
  int x=0,res=1;char ch=getchar();
  while(ch>'9'||ch<'0'){if(ch=='-')res*=-1;ch=getchar();}
  while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
  return x*res;
}

int main()
{
  freopen(FILE".in","r",stdin);
  freopen(FILE".out","w",stdout);
  while((n=gi())&&(p=gi())){
    scanf("%s",A+1);scanf("%s",B+1);
    for(int i=1;i<=n;++i){
      S[i]=S[i-1]+(A[i]!=B[i]);
      f[i]=100*S[i]-p*i;
    }
    bin[tot=1]=Mx=0;bin[n+1]=n;Ans=1-S[1];
    for(int i=1;i<=n;++i){
      if(f[i]>f[Mx]){bin[++tot]=Mx=i;continue;}
      register int l=0,r=tot,ans=n+1;
      while(l<=r){
        int mid=(l+r)>>1;
        if(f[bin[mid]]<f[i])l=mid+1;
        else ans=mid,r=mid-1;
      }
      Ans=max(Ans,i-bin[ans]);
    }
    Ans?printf("%d\n",Ans):printf("No solution.\n");
  }
  fclose(stdin);fclose(stdout);
  return 0;
}