数论学习

初等数论笔记

整除（小学奥数内容）

　　有关性质：传递性、同乘性、以及一些显然的性质。

　　　　　　　 还有b|0对于所有b≠0成立。

　　　　　　　 若(a,b)=1,a|n,b|n,则(ab)|n；

相关姿势：求出x的所有因子。这个应该没有更好的复杂度了。

void getd(int x){
  for(int i=1;i*i<=x;++i)
    if(x%i==0){
      d[++tot]=i;
      if(i*i!=x)d[++tot]=x/i;
    }
  //sort(d+1,d+tot+1);
}

求因子

余数和同余（小学奥数内容）

　　定义；模意义；

　　有关性质：传递性、同加减乘，不同除，以及一些显然的性质。

　　　　　　　试着证明一下：a%p=x,a%q=x,(p,q)=1 => a%(pq)=x；

　　　　　　　　　　　　　　尝试用到上面的定理。

　　快速幂，龟速乘等等；

　　中国剩余定理；

　　相关题目：

　　　　某校内OJ1272　　　　就是板子对吧。

　　　　HDU1788 　　　　　　思维不要江僵化了。

有关题目：

　　1.codevs1455路径

　　　　一些小处理就可以啦。

　　2.膜法数字：

　　　　n个数中必定含有1,2,3,4四个数字。求一种排列方式使其膜7为0（显然的SPJ）。

　　　　思考一下：信息学最重要的三种思想是什么？

　　　　这也许江会是你们今天最大的收获!

大胆猜想
不用证明
打表输出

素数与合数

　　定理；1都不是；2是唯一的偶质数。

　　筛法：素数的线性筛法。

　　分解质因子；spqt(n)；

　　判定：对于小数，sqrt(n)；　　

　　　　　对于大数，非完美算法 miller-rabin；对于(a,p)=1，有：

　　　　　　　　　费马小定理：如果p是质数，那么a^(p-1)≡1(mod p)；

　　　　　　　　　　　你会发现这远远不够，比如说561=3*11*17，1105=5*13*17，但无论怎样它们都...　

　　　　　　　　　补充定理：如果p是质数，那么a*a≡1(mod p)的解只有a=1或p-1。试用初中数学证明。

#include    <iostream>
#include    <cstdio>
#include    <cstdlib>
#include    <algorithm>
#include    <vector>
#include    <cstring>
#include    <queue>
#include    <ctime>
#define LL long long int
#define ls (x << 1)
#define rs (x << 1 | 1)
using namespace std;
int n;
int gi()
{
  int x=0,res=1;char ch=getchar();
  while(ch>'9'||ch<'0'){if(ch=='-')res*=-1;ch=getchar();}
  while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
  return x*res;
}
int Qpow(int d,int z,int mod)
{
  int ans=1;
  for(;z;z>>=1,d=d*d%mod)
    if(z&1)ans=ans*d%mod;
  return ans;
}
bool check(int a,int n,int t,int u)
{
  int x=Qpow(a,u,n);
  while(t--)
    {
      int y=x*x%n;
      if(y==1 && x!=1 && x!=n-1)
	return true;
      x=y;
    }
  return x!=1;
}
// check: return [n must not be a prime];
bool Mr(int n)
{
  if(n==1)return false;
  if(n==2||n==3||n==5||n==7||n==11)return true;
  if(n==4||n==6||n==8||n==9||n==10)return false;
  int m=n-1,j=0;
  while(!(m&1))m>>=1,++j; //n=1+m*2^j
  for(int t=1;t<=10;++t)   //judge 10 times
    {
      int a=rand()%(n-2)+1;
      if(check(a,n,j,m))return false;
    }
  return true;
}
int main()
{
  srand(time(NULL));
  n=gi(),printf("%s\n",Mr(n)?"Yes":"No");
  return 0;    
}

　　因数分解；唯一分解定理。

　　　　　　　威尔逊定理。逆定理。

　　　　　　　费马小定理；与欧拉定理之间的关系。(记住欧拉定理就阔以了)。

　　　　　　　因子个数；因子和(其实这个阔以筛出来)；

　　　　　　　求大整数因子算法：Fermat；Pollard Rho；

乘法逆元

　　定义；

　　性质(用途)；证明；

　　求法；单个；线性求(必须是质数)；

A[i]=-(p/i)*A[p%i];

　　NOIP2012　其实并不喜欢这种知道就是闭着眼切不知道就是玩蛋的题

　　哦对三行扩展欧几里得代码。理解什么的没必要了。(　反正我是hh　想看的话网上一大堆)

int exgcd(int a,int b,int &x,int &y)
{
    if(!b){x=1;y=0;return a;}
    exgcd(b,a%b,y,x);
    y-=a/b*x;
}
int main()
{
    int gcd=exgcd(a,b,x,y);
    // 把  ax+by=gcd(a,b) 　的解存储在x,y中。
}

　　乘法逆元是都要会求的，考点颇多。数论题和组合数学题很多都要用到它。

GCD与LCM

　　定义；

　　性质；i*j=gcd(i,j)*lcm(i,j)；

　　GCD的求法；LCM的求法；

看上去不难，但实际上... ...下面来做一道思维题

【题目名：密码  strongbox】 【64MB】 【4s】
【题目描述】
    有一个密码箱，0—n-1中的某些整数是它的密码。
    满足：如果a和b都是它的密码，那么(a+b)%n也是它的密码(a=b是合法情况)。
    欧洲皇帝QT试了k次密码，前k-1次都失败了，最后一次成功了。
    请问：该密码箱最多可能有多少种不同的密码。
【输入格式】
    输入第一行有两个正整数，分别表示n，k。
    第二行为k个非负整数，表示每次试的密码。
    保证存在合法解。
【输出格式】
    一行一个整数，表示结果。
【输入样例1】
    42 5
    28 31 10 38 24
【输出样例1】
    14
【数据规膜】
    对于10%的数据：n≤10^4，k≤100；
    另有10%的数据：n≤10^9，k≤100；
    另有10%的数据：n≤10^9，k=1；
    对于前60%的数据：k≤1000；
    对于100%的数据：1≤k≤250,000≤n≤10^14；

这道题确实思维难度颇高。我就把解题报告讲(kuai)一讲(kuai)。
首先你得推出2个东西。
1.如果x是密码，那么gcd(x,n)也是密码。
    具体证明联系"扩展欧几里得"知识。
2.如果x,y是密码，那么gcd(x,y)也是密码。
    具体证明同上。

然后我们对密码进行分析。
记尝试密码集合为a;
1.对于密码集合A，里面所有元素的gcd记作X,有X∈A;
    证明：引理2；
2.X是A中最小的元素，且X|gcd(a[k],n)；
    证明：引理2，引理1；
3.其他的元素是2X,3X,4X...⌊n/x⌋*x;
    证明：显而易见；
4.X可能有多个解，但多个解不能同时存在。所以X取解集的最小值。
    证明：引理1，答案要求；
5.X与a[j](1≤j<k)互质；
    证明：显而易见；
6.最后的答案就是⌊n/x⌋；

具体代码实现步骤是什么呢？
1.读入a后，a[k]=gcd(n,a[k]);
2.a[j]=gcd(a[j],a[k]);
    这是为了方便我们节省复杂度。
3.处理出a[k]的所有因子，制造答案可能集;
4.把所有不符合上述结论的因子删掉;
5.找到最小的答案，并输出。

具体代码我就不打了，你们想做也做不了，只能嘴巴一下。
为什么呢？
给你一句伤心的话：
Please contact lydsy2012@163.com!

欧拉函数及欧拉定理

　　欧拉函数：定义；

　　　　　　　性质；积性函数；尝试求出;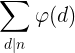

　　　　　　　　　　计算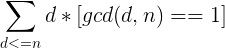和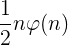

　　　　　　　欧拉函数的线性筛(积性)；O(sqrt(n))求单个欧拉函数值。

　　欧拉定理与费马小定理；

　　引子：求分母小于等于n的最简真分数的个数。

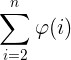不要思维江化了啊

　　1.BZOJ2705　欧拉函数。所以这是答案。

#include    <iostream>
#include    <cstdio>
#include    <cstdlib>
#include    <algorithm>
#include    <vector>
#include    <cstring>
#include    <queue>
#define LL long long int
#define ls (x << 1)
#define rs (x << 1 | 1)
using namespace std;
LL n,Ans;
LL gL()
{
  LL x=0,res=1;char ch=getchar();
  while(ch>'9'||ch<'0'){if(ch=='-')res*=-1;ch=getchar();}
  while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
  return x*res;
}
LL get(LL x)
{
  LL ans=x;
  for(LL i=2;i*i<=x;++i)
    if(x%i==0)
      {
	ans=ans/i*(i-1);
	while(x%i==0)x/=i;
      }
  if(x!=1)ans=ans/x*(x-1);
  return ans;
}
int main()
{
  n=gL();
  for(LL i=1;i*i<=n;++i)
    if(n%i==0)
      {
	if(i*i==n)Ans+=i*get(i);
	else Ans+=(i*get(n/i)+(n/i)*get(i));
      }
  printf("%lld\n",Ans);
  return 0;
}

所以有的省的省选还是有很水的题的，不像某南。

　　2. BZOJ2818 　BZOJ2190　所以这两题很水咯。

#include    <iostream>
#include    <cstdio>
#include    <cstdlib>
#include    <algorithm>
#include    <vector>
#include    <cstring>
#include    <queue>
#define LL long long int
#define Inc i*Prime[j]
using namespace std;
const int N = 10010000;
int n,Prime[N],tot,ph[N],vis[N];
LL Q[N],Ans;
int gi()
{
  int x=0,res=1;char ch=getchar();
  while(ch>'9'||ch<'0'){if(ch=='-')res*=-1;ch=getchar();}
  while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
  return x*res;
}
LL gl()
{
  LL x=0,res=1;char ch=getchar();
  while(ch>'9'||ch<'0'){if(ch=='-')res*=-1;ch=getchar();}
  while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
  return x*res;
}
void prepare()
{
  ph[1]=1;
  for(int i=2;i<=n;++i)
    {
      if(!vis[i]){Prime[++tot]=i;ph[i]=i-1;}
      for(int j=1;j<=tot;++j)
	{
	  if(Inc>N)break;vis[Inc]=1;
	  if(i%Prime[j])ph[Inc]=ph[i]*ph[Prime[j]];
	  else{ph[Inc]=ph[i]*Prime[j];break;}
	}
    }
  for(int i=2;i<=n;++i)
    Q[i]=Q[i-1]+(LL)ph[i];
}
int main()
{
  n=gi();prepare();
  for(int i=1;i<=tot;++i)
    Ans+=(2*(Q[n/Prime[i]])+1);
  printf("%lld",Ans);
  return 0;
}

#include    <iostream>
#include    <cstdio>
#include    <cstdlib>
#include    <algorithm>
#include    <vector>
#include    <cstring>
#include    <queue>
#define LL long long int
#define Inc i*Prime[j]
using namespace std;
const int N = 40100;
int n,vis[N],Prime[N],ph[N],tot,Ans;
int gi()
{
  int x=0,res=1;char ch=getchar();
  while(ch>'9'||ch<'0'){if(ch=='-')res*=-1;ch=getchar();}
  while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
  return x*res;
}
void pui(int x)
{
  if(x<10)putchar(x+'0');
  else pui(x/10),putchar(x%10+'0');
}
void shai()
{
  ph[1]=1;
  for(int i=2;i<=n;++i)
    {
      if(!vis[i]){Prime[++tot]=i;ph[i]=i-1;}
      for(int j=1;j<=tot;++j)
        {
          if(Inc>n)break;vis[Inc]=1;
          if(i%Prime[j])ph[Inc]=ph[i]*ph[Prime[j]];
          else {ph[Inc]=ph[i]*Prime[j];break;}
        }
      Ans+=ph[i];
    }Ans-=ph[n]-1;
}     
int main()
{
  n=gi();shai();
  printf("%d",Ans*2+1);
  return 0;
}

　　3. BZOJ1951　考的比较多，板子合集，还带了一点思维，是道不错的题。　　

#include    <iostream>
#include    <cstdio>
#include    <cstdlib>
#include    <algorithm>
#include    <vector>
#include    <cstring>
#include    <queue>
#define LL long long int
#define ls (x << 1)
#define rs (x << 1 | 1)
using namespace std;
const LL Mod = 999911659;
const int N = 50010;
LL n,g,M[]={0,2ll,3ll,4679ll,35617ll},Y[10];
LL J[N],A[N],Z[10];
void pL(LL x)
{
  if(x<10)putchar(x+'0');
  else pL(x/10),putchar(x%10+'0');
}
LL gL()
{
  LL x=0,res=1;char ch=getchar();
  while(ch>'9'||ch<'0'){if(ch=='-')res*=-1;ch=getchar();}
  while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
  return x*res;
}
void prepare(LL x)
{
  A[1]=J[0]=J[1]=1;
  for(LL i=2;i<x;++i)
    J[i]=J[i-1]*i%x,A[i]=((-(x/i)*A[x%i])%x+x)%x;
}
LL C(LL N,LL M,LL P)
{
  if(N<M)return 0ll;
  LL ans=J[N];
  ans*=A[J[M]];ans%=P;
  ans*=A[J[N-M]];ans%=P;
  return ans;
}
LL Lucas(LL N,LL M,LL P)
{
  if(!M)return 1ll;
  if(N<P&&M<P)return C(N,M,P);
  LL c=C(N%P,M%P,P);if(!c)return 0ll;
  LL L=Lucas(N/P,M/P,P);return c*L%P;
}
LL get(LL mod)
{
  LL ans=0;
  for(LL i=1;i*i<=n;++i)
    if(n%i==0)
      {
　　    ans+=Lucas(n,i,mod);ans%=mod;
   　　 if(i*i!=n)ans+=Lucas(n,n/i,mod),ans%=mod;
      }
  return ans;
}
LL Qpow(LL d,LL z)
{
  LL ans=1;
  for(;z;z>>=1,d=d*d%Mod)if(z&1)ans=ans*d%Mod;
  return ans;
}
int main()
{
  n=gL();g=gL()%Mod;
  if(g==0){pL(0);return 0;}
  for(int t=1;t<=4;++t)
    {
      prepare(M[t]);
      Y[t]=get(M[t]);
      Z[t]=((Mod-1)/M[t])*A[((Mod-1)/M[t])%M[t]];
      Y[0]+=Y[t]*Z[t]%(Mod-1);Y[0]%=(Mod-1);
    }
  return pL(Qpow(g,Y[0])),0;
}

　　4. BZOJ1408 提示：积性，结合率，递×。

#include    <iostream>
#include    <cstdio>
#include    <cstdlib>
#include    <algorithm>
#include    <vector>
#include    <cstring>
#include    <queue>
#define LL long long int
#define ls (x << 1)
#define rs (x << 1 | 1)
using namespace std;
const LL Mod = 10000;
LL F[1010][1010],Ans1,Ans2,m,k;
int gi()
{
  int x=0,res=1;char ch=getchar();
  while(ch>'9'||ch<'0'){if(ch=='-')res*=-1;ch=getchar();}
  while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
  return x*res;
}
void pL(LL x)
{
  if(x<0)putchar('-'),pL(-x);
  if(x<10)putchar(x+'0');
  else pL(x/10),putchar(x%10+'0');
}
void pc(){putchar('\n');}
LL gL()
{
  LL x=0,res=1;char ch=getchar();
  while(ch>'9'||ch<'0'){if(ch=='-')res*=-1;ch=getchar();}
  while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
  return x*res;
}
LL Qpow(LL d,LL z)
{
  LL ans=1;
  for(;z;z>>=1,d=d*d%Mod)if(z&1)ans=ans*d%Mod;
  return ans;
}
int main()
{
  k=gL();m=1;
  for(LL i=1;i<=k;++i)
    {
      LL p=gL(),e=gL();
      m=m*Qpow(p,e)%Mod;
      if(p==2)continue;
      LL ans1=(Ans1+(Ans2+1)*(p-1))%Mod;
      LL ans2=(Ans2+Ans1*(p-1))%Mod;
      Ans1=ans1;Ans2=ans2;
    }
  pL(Ans2);pc();pL(Ans1);pc();pL(((m-Ans1-Ans2-1)%Mod+Mod)%Mod);
  return 0;
}

　　最后来道水题放放松。李电出过的题，大家应该都切过。

　　　BZOJ3884

#include    <iostream>
#include    <cstdio>
#include    <cstdlib>
#include    <algorithm>
#include    <vector>
#include    <cstring>
#include    <queue>
#define LL long long int
using namespace std;
int n,p;
int gi()
{
  int x=0,res=1;char ch=getchar();
  while(ch>'9'||ch<'0'){if(ch=='-')res*=-1;ch=getchar();}
  while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
  return x*res;
}
void pL(int x)
{
  if(x<0)putchar('-'),pL(-x);
  if(x<10)putchar(x+'0');
  else pL(x/10),putchar(x%10+'0');
}
int Qpow(int d,int z,int Mod)
{
  int ans=1;
  for(;z;z>>=1,d=(LL)d*d%Mod)if(z&1)ans=(LL)ans*d%Mod;
  return ans;
}
int phi(int x)
{
  int Txd=x;
  for(int i=2;i*i<=x;++i)
    if(x%i==0)
      {
        Txd-=Txd/i;
        while(x%i==0)x/=i;
      }
  if(x>1)Txd-=Txd/x;
  return Txd;
}   
int f(int p)
{
  if(p==1)return 0;int x=phi(p);
  return Qpow(2,x+f(x),p);
}
int main()
{
  int T=gi();
  while(T--)pL(f(gi())),putchar('\n');
  return 0;
}

原根与离散对数

　　先来看看这道题怎么写。

　　某校内OJ 1508。求 a^x≡1 (mod b)。

　　当时我做这题时还太naive，现在想想很简单是吧？

　　介绍一下原根和离散对数。(你们随便听听就够了,有点超)

　　原根：

　　　　对于2个互质的数a,b，由欧拉定理知，必定存在x≤φ(b),使a^x≡1 (mod b)；

　　　　x记作a对模m的阶，记作δ_m(a);(应该是长这个吧)

1^1≡1(modn),1对模n的阶为1；
2^2≡1(mod3),2对模3的阶为2；
5^6≡1(mod7),5对模7的阶为6；
2^3≡1(mod7),2对模7的阶为3；

　　　　由此，定义Ord_m(a)为使得a^x≡1 (mod m) 的最小整数解x；

　　　　如果有Ord_ma=φ(m),则称a是模m的一个原根。

　　　　我知道刚刚看完的肯定一脸蒙蔽... ...我也是。

　　原根的有关性质，我蒯了一点。

　　　　(1).具有原根的数一定是：2,4,p^n,2(p^n)，其中p为奇素数。

　　　　(2).m的最小原根大小是O(m^0.25)的。所以有些东西你枚举就够了(惨疼的教训)。

　　　　(3).如果模m有原根，那么它有φ(φ(m))个原根。(防止有人出结论题)。

　　求原根的方法：

你们不是已经知道了吗？

离散对数

　　初等代数中的对数运算，定义如果有a^x=b,则称x是以a为底的对数，记作log_ab；

　　在同余关系中也有类似的问题。给定n,a,b，如何求解x使a^x≡b (mod n);

　　这一问题也被称作离散对数问题。我们只讨论n为素数的情况。

　　先来讨论暴力怎么做？

　　由欧拉定理，我们知道0~n-1内必有一解，递推即可，复杂度O(n);

　　但这样并不是很好的算法，下面给出一种O(比n小)的算法。

首先计算出x=0,1,2...m时a^x (mod n)的值。

设a^k≡b (mod n)；设 k=p*m+q(q<m)；枚举p；

对于一个枚举出的p，a^p*m是一定且可求的。

则可以改写成：　a^p*m+q≡b (mod n)；

　　　继续改：　a^q*a^pm≡b (mod n)；

　　　再一步：　a^q*(a^m)^p≡b (mod n)；

　　　设T=(a^m)^p，就有：

　　　　　　　　T*a^q≡b (mod n)；

　　　你就可以用exgcd求出T；

　　　那么问题就在于求q上。聪明的你可以用很多种方法解决这个问题。。。

　　　这种分块用基本不等式算出m取到sqrt(n)时复杂度最优秀。。。

练习题：

　　BZOJ2956 模积和；

　　BZOJ1407 Savage(NOI 2002 荒岛野人)；

　　NOIP2014 Day2T3 解方程，同BZOJ2742 Akai的数学作业；

　　神题之圆上的整点；

　　神题之数论之神CJK；

　　其实上面的题目我一个都不会。

posted @ 2017-03-26 18:23 Fenghr 阅读(343) 评论(0) 编辑收藏举报

刷新页面返回顶部

Fenghr

答案是永不止步

数论学习

初等数论笔记

公告