进制转换
十进制转其他进制
Eg:十进制转二进制
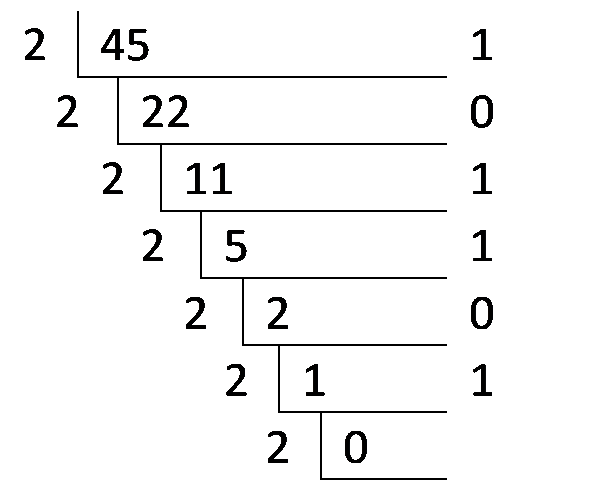
我们通常采用短除法,进行除二取余,逆序排列,如下面计算45的二进制数101101的步骤:
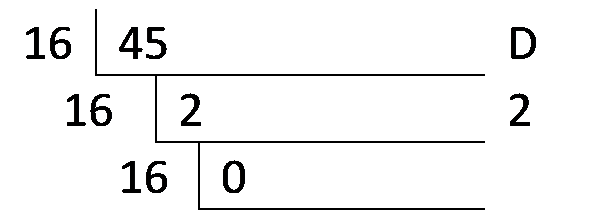
同样,当我们要将十进制转换为x进制时,我们只需要将除数改为x就行了,如下面计算45转成十六进制2D的步骤:
其他进制转十进制
二进制转十进制
我们先要对数字按低位到高位从零开始标号
| 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 | 1 |
| 然后可以得出十进制:\(1\times2^5+0\times2^4+1\times2^3+1\times2^2+0\times2^1+1\times2^0=45\) |
十六进制转十进制
同样的方法
| 1 | 0 |
|---|---|
| 2 | D |
| 然后可以得出十进制:\(2\times16^1+13\times2^0=45\) | |
| 所以当我们要把x进制转为十进制时,也是使用同样的方法 | |
| n | ... |
| :-: | :-: |
| \(a_n\) | ... |
| 得出十进制:\(a_n \times x^n+...+a_4 \times x^3+a_3 \times x^2+a_2 \times x^1+a_1 \times x^0\) |
二进制、八进制、十六进制的互相转换
由于二进制、八进制、十六进制都是2的次方进制,所以它们之间的互相转化能够使用特殊的方法
二进制转十六进制
例如转换二进制数101101,我们会将其从最低位开始四位四位分割,然后将每一个被分割的部分转换为十六进制,如下所示:
| 0010 | 1101 |
| 2 | 13 |
| 2 | D |
十六进制转二进制
例如转换十六进制数2D,反过来使用二进制转十六进制的方法,便可以实现:
| 2 | D |
| 2 | 13 |
| 0010 | 1101 |
二进制与八进制的互转
如果我们想把二进制转换为八进制,只需要将相应的二进制数从最低位起三位三位分割,然后将每一个被分割的部分转换为八进制。
如果是八进制转换为二进制,则反过来使用以上方法。
得到普遍规律
\(x\)进制转\(x^m\)进制:将相应的\(x\)进制数从最低位起\(m\)位\(m\)位分割,然后将每一个被分割的部分转换为\(x^m\)进制
\(x^m\)进制转\(x\)进制:将相应的\(x^m\)进制数逐位转换为\(x\)进制数


