机器学习理论决策树理论第二卷
决策树内容来至于《统计学习与方法》李航,《机器学习》周志华,以及《机器学习实战》Peter HarringTon,相互学习,不足之处请大家多多指教!
本卷的大纲为
1 CART 算法
1.1 CART 回归树
1.2 CART 分类树
2 CART 剪枝
3 总结
1 CART算法
CART分类与回归树(classification and regression tree,CART)模型室友Breiman等人1984年提出,是应用广泛的决策树方法,CART同样由特征选择,树的生成以及剪枝组成,可以用于分类,也可以用于回归。
CART树的生成:决策树的生成就是递归的构建二叉决策树的过程,对回归树使用平方误差最小的准则,对分类树使用基尼指数最小化准则,进行特征选择,生成二叉树。
1.1回归树的生成(对应连续变量)
假设X与Y分别为输入和输出变量,并且Y是连续变量,给定训练数据集:
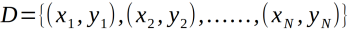
一个回归树对应着输入空间(特征空间)的一个划分以及在划分的单元上的输出值,假设已将输入空间划分为M个单元R1,R2,……,Rm,并且每个单元Rm上都有一个固定的输出值Cm,于是回归树模型可表示为:

当输入空间的划分确定后,可以用平方误差:
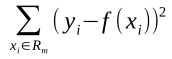
来表示回归树对训练数据的预测误差,用平方误差最小的准则求解每个单元上的最优输出值,单元Rm上的输出值Cm的最优值C是Rm上的所有输入实例Xi对应输出Yi的均值。即
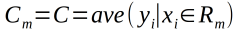
输入空间的划分:选择第J个变量x(J)和他的取值S,作为切分变量和切分点,并定义两个区域:

让后寻找最优的切分变量以及最优的切分点,具体求解
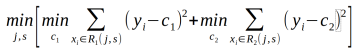
对固定输入变量J可以找到最优切分点s:
![]()
遍历所有的输入变量,找到最优的切分变量j,构成一对(j,s),依次将输入空间划分为2个区域,接着对每个区域重复划分,直到满足条件为止,这样的回归树通常称为最小二乘回归树。
1.2最小二乘回归树的生成算法:
输入:训练数据集D;
输出:回归树f(x)
在训练数据集所在的输入空间中,递归的将每个区域划分为2个子区域并决定每个子区域上的输出值,构建二叉树:
(1)选择最优切分变量j与切分点s,求解:

遍历变量j,对固定的切分变量j扫描切分点s使得上述式子最小化。输出该值对(j,s)。
(2)用选定的对(j,s)划分区域并决定相应的输出值:
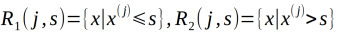

(3)继续对两个子区域调用步骤1和步骤2,直到满足条件。
(4)将输入空间划分为M个区域R1,R2,……,Rm,生成决策树:

2 分类树的生成
分类树使用基尼指数作为最优特征,同时决定该特征的最优二值切分点。
分类问题中,假设K个类别,样本属于第K类的概率为Pk,则概率分布的基尼系数为:

对于二分类问题,若样本点属于第一个类别的概率是P,则概率分布的基尼指数为:
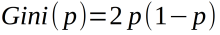
对于给定的样本集合D,其基尼系数为:Ck是第K类样本的个数,k是类的个数
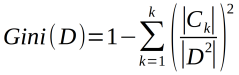
如果样本集合D根据特征A是否取得某一个可能的a被分为2份D1,和D2,则在特征A条件下,集合D的基尼指数定位为:
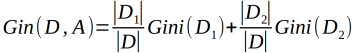
基尼指数表示了集合D的不确定性,基尼指数Gin(D,A)表示A= a分割后集合D的不确定性,基尼指数越大,样本集合的不确定性也越大,这一点和熵类似。
基尼系数和熵的关系,可以理解为基尼系数是熵在x=1处的一节泰勒展开
使用python画出基尼指数,熵之半曲线,分类误差曲线如图所示:
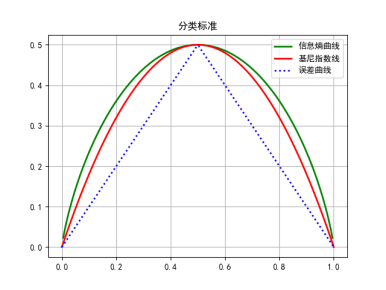
相关代码为
#!/usr/bin/python #-*-encoding:utf-8 -*- import numpy as np import matplotlib as mpl import matplotlib.pyplot as plt import math mpl.rcParams['font.sans-serif'] = [u'SimHei'] mpl.rcParams['axes.unicode_minus'] = False def entropy(p): return 0.5*( -p*np.log2(p) - (1-p)*np.log2(1-p)) def jini(p): return 2*p*(1-p) def wucha(p): return 1-np.max(np.vstack((p,1-p)),0) if __name__=="__main__": p = np.linspace(0,1,200) y = entropy(p) y2 = jini(p) y3 = wucha(p) fig = plt.figure(facecolor='w') plt.title(u"分类标准") plt.plot(p,y,'g-',linewidth=2,label=u'信息熵曲线') plt.plot(p, y2, 'r-', linewidth=2, label=u'基尼指数线') plt.plot(p, y3, 'b:', linewidth=2, label=u'误差曲线') plt.legend(loc='upper right') plt.grid(True) plt.show()
2.2 CART生成算法
输入:训练数据D,停止计算条件
输出:CART决策树
具体算法如下为:根据训练数据集,从根节点开始,递归的对每个节点进行以下操作,构建二叉树:
(1)设训练集数据集为D,计算现有特征对数据集的基尼指数,此时,对每个特征A,对其可能的每个取值,根据样本点对A=a的测试为是或否将D分割为D1和D2两部分,之后计算A的基尼系数:
(2)在所有可能的特征A以及他们所有可能的切分点a中,选择基尼指数最小的特征及其对应的切分点作为最优特征和最优切分点,依最优特征和最优切分点,从现结点生成两个子节点,将训练数据集依
征分配到两个子节点中去。
(3)对两个子节点递归调用(1)(2)直到满足停止条件
(4)生成CART决策树。
3 CART剪枝
CART剪枝算法从完全生长的决策树的底端剪去一些子树,使得决策树变得简单,从而能够对未知数据有更准确的预测,CART剪枝算法由两步组成,首先从生成算法产生的决策树T0底端开始不断的剪
枝直到T0的根节点,形成一个子树序列{T0,T1,T2……Tn};然后通过交叉验证法验证数据集上对子树进行测试,从中选取最优子树。
步骤1:剪枝,形成一个子树序列
具体的:从整个树的T0底端开始剪枝,对T0的任意内部结点t,对T0中的每个内部结点t,计算
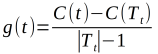
他表示剪枝后整体损失函数减少的程度,在T0中剪去g(t)得到最小的Tt,将得到的子树作为T1.同时,将最小的g(t)设置为α1,T1为区间[α1,α2)的最优子树。
步骤2:在剪枝得到的子树序列T0,T1,……,Tn中,通过交叉认证选取最优子树。
具体的,利用独立的验证数据集,测试子树序列T0,T1,T2……,Tn中各个子树的平均误差或者基尼指数,平方误差或者基尼指数最小的决策树认为是最优决策树,在子树序列中,每颗子树T1,T2,
……,Tn应一个参数α1,α2,……,αn,所以当最优子树确定时,对应的αk也确定了,即得到了最优子树。
4 总结
决策树算法包括三部分:特征选择,树的生成和树的剪枝,常用的算法有ID3,ID4.5,CART算法
特征选择的目的在于选取对训练数据能够分类的特征,特征的选择的关键是其准则,常见的准则如下:
(1)样本集合D对特征A的信息熵增益(ID3)其中H(D)是数据集D的熵,H(Di)是数据集Di的熵,H(D|A)是数据集D对特征A的条件熵,Di是D中特征A取第i个的样本子集,Ck是D中属于第k类的样本子
集,是特征A取值的个数,k是类的个数。
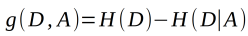

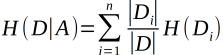
(2)样本集合D对特征A的信息增益比(C4.5),其中g(D,A)是信息增益,H(D)是数据集D的熵
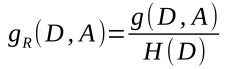
(3)样本集合的基尼系数(CART算法)

特征A下的基尼系数:

决策树的生成:通常使用信息增益最大,信息增益比最大,或者基尼指数最小作为特征选择的准这,决策树的生成往往是通过计算信息增益或者其他指标,从根节点开始,递归的产生决策树,这相当于
信息增益或者其他准则不断的选取局部最优的特征,或将训练集分割为能够基本正确分类的子集。
决策树的剪枝:由于生成的决策树存在过拟合的问题,需要对他进行剪枝,通常决策树剪枝有有预剪枝和后剪枝。主要考察剪枝前后验证集的精度。或者极小化决策树整体的损失函数。




