机器学习理论决策树算法第一卷
决策树算法内容来至于《统计学习与方法》李航,《机器学习》周志华,以及《机器学习实战》Peter HarringTon,相互学习,不足之处请大家多多指教
本卷的大纲为
1 决策树的概念
2 特征选择,信息熵,条件熵
3 决策树的生成
4 决策树的剪枝
1 决策树的概念
决策树是一颗基于分类与回归的方法,本章主要讨论分类的决策树。决策树的模型呈树形结构,在分类问题中,表示基于特征对实例进行分类的过程。
决策树的学习过程包括:特征选择,决策树的生成,和决策树修剪。
决策树的优点:模型具有可读性,分类速度快,学习时,利用训练数据,根据损失函数最小化的原则建立决策树模型,预测时,对新的数据,利用决策树模型进行分类。
决策树由结点和有向边组成,结点有两个类型:内部结点和叶节点,内部结点表示一个特征或者属性,叶结点表示一个类别。
决策树可以转换为if-then模型,内部结点的特征对应规则的条件,叶节点表示对应规则下的结论。
决策树的损失函数通常是正则化的最大似然函数。决策树学习的策略是以损失函数为目标函数的最小化。
决策树构建的过程:
(1)开始构建根结点,将所有训练数据都放在根结点上。
(2)选择一个最优特征,按照这个特征将训练数据集分割成子集,使得各个子集有一个在当前条件下的最好分类。
(3)如果这个子集已经基本上正确分类,那么构建叶节点。
(4)如果还有子集不能被基本正确分类,那么就对这些子集选着新的最优特征,继续对子集进行分割。递归下去直到所有训练数据的子集被基本正确分类。最后每个子集都被分到叶节点上。形成一
个决策树。
决策树学习的过程包括特征选择,决策树的生成,以及决策树的剪枝,由于决策树表示一个条件概率分布,所以深浅不同的决策树对应不同复杂度的概率模型,决策树的生成对应模型的局部选择
决策树的剪枝对应模型的全局选择,决策树的生成只考虑局部最优,相对的,决策树的剪枝表示全局最优。
2 特征选择,信息熵,条件熵
特征选择在于选取对训练数据具有分类特征的特征,提高决策树的学习效率,特征选择准则基于信息增益和信息增益比。
2.1信息熵
信息熵的概念:熵表示随机变量不确定性的度量,熵越大,随机变量的不确定性就越大。信息熵的定义如下:
设X是有限个离散随机变量,其概率分布为:
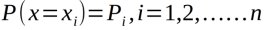
随机变量X的熵定义为:
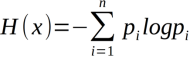
通常,如果5.1中的对数以2为底,则信息熵的单位为比特,以自然对数为底,则信息熵的单位为钠特(nat).
当随机变量只取二个值的时候,X的分布为
P(x=1) = p
P(x=0) = 1-p
H(x)=-plog2p-(1-p)log2(1-p)
此时熵的曲线为:
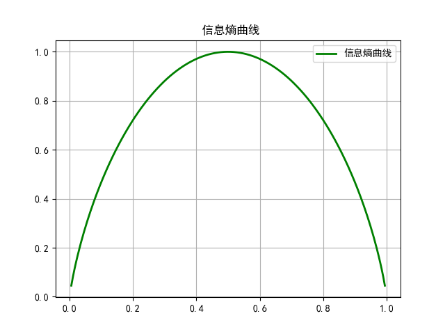
对应的Python代码为:
#!/usr/bin/python #-*-encoding:utf-8 -*- import numpy as np import matplotlib as mpl import matplotlib.pyplot as plt import math mpl.rcParams['font.sans-serif'] = [u'SimHei'] mpl.rcParams['axes.unicode_minus'] = False def entropy(p): return -p*np.log2(p) - (1-p)*np.log2(1-p) if __name__=="__main__": p = np.linspace(0,1,200) y = entropy(p) fig = plt.figure(facecolor='w') plt.title(u" 信息熵曲线") plt.plot(p,y,'g-',linewidth=2,label=u'信息熵曲线') plt.legend(loc='upper right') plt.grid(True) plt.show()
2.2条件熵
设随机变量(x,y),其联合概率分布为
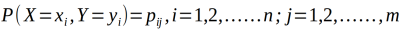
条件熵的H(Y|X)表示在已知随机变量X的条件下,随机变量Y的不确定性
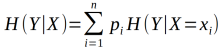
当熵和条件熵有数据估计(特别是极大似然估计)得到时,所对应的熵为经验熵,对应的条件熵为经验条件熵。
2.3 信息增益
信息增益表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。
信息增益的定义如下:特征A对训练数据集D的信息增益g(D,A),定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差,即
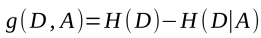
一般的,熵H(Y)和条件熵(Y|X)之差称之为互信息,决策树学习中的信息增益等价于训练数据集中类与特征的互信息。
根据信息增益选取特征的方法是:对数据集(或者子集)D,计算其每个特征的信息增益,并比较他们的大小,选择信息增益最大的特征。
2.4信息熵增益比:
以信息熵增益作为划分训练数据集的特征,存在偏向与特征选取比较多的特征的问题,使用信息熵增益比可以对这个问题进行矫正,信息熵增益比的定义如下:
特征A对训练数据集D的信息增益比gR(D,A)定义为其信息增益g(D,A)与训练数据集D关于特征A的值的熵HA(D)之比:
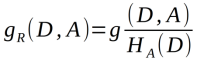
其中:
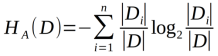
3决策树的生成
决策树主要有ID3生成算法和C4.5生成算法,ID3算法的核心在于决策树各个节点上运用信息增益选择决策树,C4.5选择信息熵增益比为准则选择决策树。
3.1 ID3算法
ID3决策树算法的核心是在决策树的各个节点上运用信息熵增益作为选择特征,递归的构建决策树,具体算法流程是:
从根节点开始,对结点计算所有可能的特征的信息增益,选择信息增益最大的特征作为节点的特征,由该特征的不同取值建立子节点,在对子节点递归的调用上面的方法,构建决策树,直到所有的特征
信息增益均很小或者没有特征可以选择为止,得到最后一个决策树。ID3相当于用极大似然法进行概率模型的估计。
3.2 C4.5算法
C4.5算法决策树算法的核心是在决策树的各个节点上运用信息熵增益比作为选择特征,递归的构建决策树,具体算法流程是:
从根节点开始,对结点计算所有可能的特征的信息增益比,选择信息增益比最大的特征作为节点的特征,由该特征的不同取值建立子节点,在对子节点递归的调用上面的方法,构建决策树,直到所有的
征的信息增益比均很小或者没有特征可以选择为止,得到最后一个决策树。
4决策树的剪枝
决策树生成的算法递归的产生决策树,直到不能继续下去为止,这样产生的决策树往往对训练数据的分类很准确,对未知的测试数据分类不准确,出现过拟合的情况,过拟合的原因在于学习时候过多
考虑如何提高训练数据的正确分类,构造了过于复杂的决策树,解决和个问题是对决策树进行剪枝。
决策树剪枝的策略有预剪枝和后剪枝。主要考察剪枝前后验证集的精度。或者极小化决策树整体的损失函数。重点关注:后剪枝
4.1后剪枝
策略:极小化决策树整体的损失函数或者是代价函数来实现,等价于正则化极大似然估计。设树T的叶节点个数为|T|,t是树T的叶节点,该叶节点有NT个样本,其中k类的样本点有Ntk个k=1,2,3,4……k,决策树的损失函数为
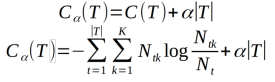
C(T)表示模型对训练数据的预测误差,即模型对训练数据的拟合程度,|T| 表示模型的复杂程度,参数α≥0 控制两者之间的影响,通常较大的α 促使选择简单的模型树,较小的α 促使选择复杂的模型树
α=0表示自是考虑模型和训练数据的拟合程度,不考虑模型的复杂度。
剪枝就是当α确定时候,选择损失函数最小的模型,即损失函数最小的子树,当α确定时,子树越大,往往训练数据拟合越好,但是模型的复杂程度也越高,反之,子树越小,模型复杂度越低,损失数正好平衡二者的关系。
4.2 树的剪枝算法
输入:生成算法产生的整个树T,参数α
输出:修剪后的子树T
算法流程:
(1)计算每个结点的经验熵
(2)递归向上的从树的叶节点进行回缩
(3)如果父节点的损失函数C(T)小于子节点的损失函数C(T),则父节点变回新的叶节点。
(4)返回2继续执行,直到不能继续为止,得到损失函数最小的子树T
优点:后剪枝决策树通常比预剪枝决策树保留更多的分支,一般情况下,后剪枝决策树的欠拟合的风险很小,泛化性能往往优于预剪枝的决策树。但是后剪枝决策树需要在完全生成决策树后进行,并自底向上对树中每个非叶节点进行考察,因此训练的时间开销要比未剪枝决策树和预剪枝决策树都要大得多。
相互学习,不足之处,请多多指教!




