深度学习-练习2 多变量线性回归
多变量线性回归
在这个练习中,我们主要解决的问题是房价的数据,在数据集中http://openclassroom.stanford.edu/MainFolder/courses/MachineLearning/exercises/ex3materials/ex3Data.zip
数据是Portland, Oregon的房价数据 共47个,变量是房价面积和卧室的个数,预测量为房价数据。
>> x = load('ex3x.dat'); >> y = load('ex3y.dat'); >> m = length(y); >> x = [ones(m, 1), x];
下面我们对所有的特征进行缩放,将所有特征的尺度缩放到-1到1之间,我们的做法是求均值和标准差。
通过原值减去均值之后除以标准差得到。具体代码如下:
>> sigma = std(x); >> mu = mean(x); >> x(:,2) = (x(:,2) - mu(2))./ sigma(2); >> x(:,3) = (x(:,3) - mu(3))./ sigma(3);
下面我们开始使用梯度下降法
这一部分跟单变量线性回归类似,不同的是这边变成了两个变量。
下面代价函数:
批量梯度下降算法 迭代规则是:
在前面我们给出了学习率为0.7,在这边我们要计算学习率通过代价函数。
学习率的范围大概如下:
具体的就是我们以另外一种向量的形式定义代价函数
这边理解1Xm 与mX1 两个向量相乘。
具体如下:
这边要说的是对于matlab之类的工具,处理向量,矩阵更加的优化,因此能转成向量矩阵运算的转成向量矩阵运算。
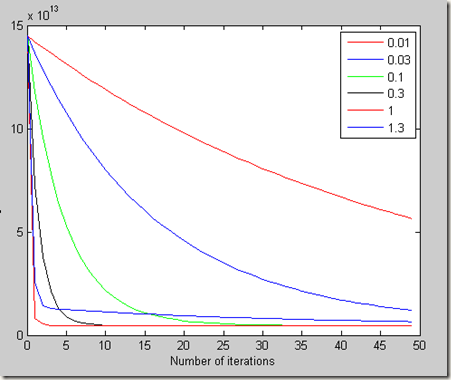
下面我们给出初始学习率,让其迭代100次,将迭代最终形成的图画出。
我们可以看出在学习率为1的时候,收敛速度最快,最容易达到局部最小值,因此使用学习率为1.
具体全部代码如下:
x = load('ex3x.dat'); y = load('ex3y.dat'); m = length(y); x = [ones(m, 1), x]; sigma = std(x); mu = mean(x); x(:,2) = (x(:,2) - mu(2))./ sigma(2); x(:,3) = (x(:,3) - mu(3))./ sigma(3); MAX_ITR = 100; sample_num = size(x,1); figure; alpha = [0.01, 0.03, 0.1, 0.3, 1, 1.3]; plotstyle = {'b', 'r', 'g', 'k', 'b-', 'r-'}; theta_final = zeros(size(x(1,:)))'; for alpha_i = 1:length(alpha) theta = zeros(size(x(1,:)))'; J = zeros(MAX_ITR, 1); for i = 1: MAX_ITR J(i) = (0.5 * sample_num).* (x*theta - y)'* (x * theta - y); grad = (1/sample_num).*x'*(x*theta-y); theta = theta - alpha(alpha_i).*grad; end plot(0:49, J(1:50), char(plotstyle(alpha_i))); hold on; if( 1 == alpha(alpha_i)) theta_final = theta; end end legend('0.01','0.03','0.1','0.3','1','1.3'); xlabel('Number of iterations'); ylabel('Cost J'); price_gred_descend = [1 (1650-mu(2))/sigmax(2) (3-mu(3)/sigmax(3))]* theta_final;
最终预测结果为
price_gred_descend =
2.9935e+05
另外我们再使用基本的方程求解,更前面单变量线性回归一样:
price_normal =
2.9308e+05
具体代码:
theta_normal = (x_unscaled' * x_unscaled)\x_unscaled' * y; price_normal = dot(theta_normal, [1, 1650, 3]);
这边x_unscaled在没有改变的时候赋值。
这样多变量的线性回归就结束了,主要学习的时候,学习率的选择。



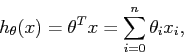
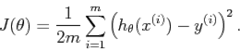
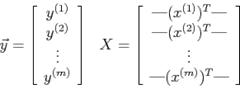

 浙公网安备 33010602011771号
浙公网安备 33010602011771号