kd树分析

kd树的应用很广，在图像特征匹配方面，也就是最终应用到图像设别，图像检索方面。对于地图的应用，像附近点搜索功能，对于三维当中的，碰撞检测，光线跟踪等等。

总的来说呢，kd树就是一个搜索策略。

kd树搜索什么呢，首先介绍一下kd树

Kd-树是K-dimension tree的缩写，是对数据点在k维空间（如二维(x，y)，三维(x，y，z)，k维(x1，x2，x3..)）中划分的一种数据结构，主要应用于多维空间关键数据的搜索（如：范围搜索和k近邻查询）。而对于特征点匹配来说的话，其本质上也是属于通过距离的大小在高维空间中判断两者的相似性。

范围搜索就是给定查询点以及查询的距离的阈值，从数据集中找出所有与查询点距离小于查询距离阈值的数据。

k近邻查询就是给定查询点，和正整数K，从数据集中找到距离查询点最近的K个数据，当K=1时，为最近邻查询。

本文参考http://underthehood.blog.51cto.com/2531780/687160

http://blog.csdn.net/v_july_v/article/details/8203674

http://www.leexiang.com/kd-tree

跟他们的思路一样，为了引出k-d树，先说一说k近邻算法。

K近邻算法，即K-Nearest Neighbor algorithm，简称KNN算法。KNN算法和K-Means算法不同的是，K-Means算法用来聚类，用来判断哪些东西是一个比较相近的类型，而KNN算法是用来做归类的，也就是说，有一个样本空间里的样本分成很几个类型，然后，给定一个待分类的数据，通过计算接近自己最近的K个样本来判断这个待分类数据属于哪个分类。你可以简单的理解为由那离自己最近的K个点来投票决定待分类数据归为哪一类。

看这么一个图

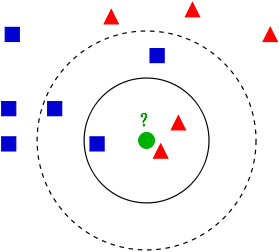
如图所示，有两类数据红色三角跟蓝色正方形，然后一个绿色的圆，来判断这个圆属于哪一类数据。这边采用欧式距离。

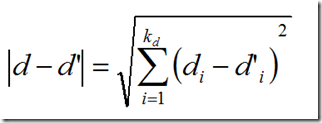其中di是向量d的第i个分量。

如果K=3.则红色2个，绿色1个，根据统计的方法，则绿色属于红色。

如果K=5.则绿色3个，红色2个，则绿色属于蓝色类。

而这个怎么选，到时根据各自的权重再来分析。这边以后再分析。引用一段话

李航博士的一书「统计学习方法」上所说：

1. 如果选择较小的K值，就相当于用较小的领域中的训练实例进行预测，“学习”近似误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是“学习”的估计误差会增大，换句话说，K值的减小就意味着整体模型变得复杂，容易发生过拟合；
2. 如果选择较大的K值，就相当于用较大领域中的训练实例进行预测，其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大。这时候，与输入实例较远（不相似的）训练实例也会对预测器作用，使预测发生错误，且K值的增大就意味着整体的模型变得简单。
3. K=N，则完全不足取，因为此时无论输入实例是什么，都只是简单的预测它属于在训练实例中最多的累，模型过于简单，忽略了训练实例中大量有用信息。

    在实际应用中，K值一般取一个比较小的数值，例如采用交叉验证法（简单来说，就是一部分样本做训练集，一部分做测试集）来选择最优的K值。

下面面临的问题就是怎么查询的问题。

很容易想到的是穷举法，也就是将数据集中的点跟查询点逐一比较，取最小的值，但是当数据量特别大的时候，这种方法的耗时就很可观了。

这么我们想到的是利用数据本身的信息，因为实际数据一般都会呈现簇状的聚类形态，因此我们想到建立数据索引，然后再进行快速匹配。

索引树是一种树结构索引方法，其基本思想是对搜索空间进行层次划分。k-d tree是索引树中的一种典型的方法。

1975年，来自斯坦福大学的Jon Louis Bentley在ACM杂志上发表的一篇论文：Multidimensional Binary Search Trees Used for Associative Searching 中正式提出和阐述的了如下图形式的把空间划分为多个部分的k-d树。

好的，k-d树是一种空间划分树，也就是把整个空间划分为特定的几个部分，然后在特定空间的部分内进行相关搜索操作，大体如下:

pointList = [(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)] tree = kdtree(pointList)

下面主要说一说kd树的构建，主要参考《图像局部不变性特征与描述》这边书。

Kd-树是一个二叉树，每个节点表示的是一个空间范围。下表表示的是Kd-树中每个节点中主要包含的数据结构。Range域表示的是节点包含的空间范围。Node-data域就是数据集中的某一个n维数据点。分割超面是通过数据点Node-Data并垂直于轴split的平面，分割超面将整个空间分割成两个子空间。令split域的值为i，如果空间Range中某个数据点的第i维数据小于Node-Data[i]，那么，它就属于该节点空间的左子空间，否则就属于右子空间。Left，Right域分别表示由左子空间和右子空间空的数据点构成的Kd-树。

域名	数据类型	描述
Node-Data	数据矢量	数据集中某个数据点，是n维矢量
Range	空间矢量	该节点所代表的空间范围
Split	整数	垂直于分割超面的方向轴序号
Left	Kd-tree	由位于该节点分割超面左子空间内所有数据点构成的Kd-树
Right	Kd-tree	由位于该节点分割超面左子空间内所有数据点构成的Kd-树
Parent	Kd-tree	父节点

构建Kd-树的伪码为：

算法：构建Kd-tree

输入：数据点集Data_Set，和其所在的空间。

输出：Kd，类型为Kd-tree

1 if data-set is null ,return 空的Kd-tree

2 调用节点生成程序

（1）确定split域：对于所有描述子数据（特征矢量），统计他们在每个维度上的数据方差，挑选出方差中最大值，对应的维就是split域的值。数据方差大说明沿该坐标轴方向上数据点分散的比较开。这个方向上，进行数据分割可以获得最好的分辨率。

（2）确定Node-Data域，数据点集Data-Set按照第split维的值排序，位于正中间的那个数据点 被选为Node-Data，Data-Set` =Data-Set\Node-data

3 dataleft = {d 属于Data-Set` & d[:split]<=Node-data[:split]}

   Left-Range ={Range && dataleft}

  dataright = {d 属于Data-Set` & d[:split]>Node-data[:split]}

  Right-Range ={Range && dataright}

4 :left =由（dataleft,LeftRange）建立的Kd-tree

   设置:left的parent域（父节点）为Kd

   ：right =由（dataright,RightRange）建立的Kd-tree

设置：right的parent域为kd。

 

举一个简单直观的实例来介绍k-d树构建算法。假设有6个二维数据点{(2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)}，数据点位于二维空间内，如下图所示。为了能有效的找到最近邻，k-d树采用分而治之的思想，即将整个空间划分为几个小部分，首先，一条红线将空间一分为二，然后在两个子空间中，两条蓝直线又将整个空间划分为四部分，最后红直线将这四部分进一步划分。

具体步骤如下：

1. 确定：split域=x。具体是：6个数据点在x，y维度上的数据方差分别为39，28.63，所以在x轴上方差更大，故split域值为x；
2. 确定：Node-data = （7,2）。具体是：根据x维上的值将数据排序，6个数据的中值(所谓中值，即中间大小的值)为7，所以Node-data域位数据点（7,2）。这样，该节点的分割超平面就是通过（7,2）并垂直于：split=x轴的直线x=7；
3. 确定：左子空间和右子空间。具体是：分割超平面x=7将整个空间分为两部分：x<=7的部分为左子空间，包含3个节点={(2,3),(5,4),(4,7)}；另一部分为右子空间，包含2个节点={(9,6)，(8,1)}；

最终生成的kd树如下：

这里先以一个简单的实例来描述最邻近查找的基本思路。

星号表示要查询的目标点（2.1,3.1）。通过二分搜索，顺着搜索路径很快就能找到最邻近的近似点，即叶子节点（2,3）。而找到的叶子节点并不一定就是最邻近的，最邻近肯定距离目标点更近，应该位于以目标点为圆心且通过叶子节点的圆域内。为了找到真正的最近邻，还需要进行回溯操作：算法沿搜索路径反向查找是否有距离目标点更近的实例点。此例中先从（7,2）点开始进行二分查找，然后到达（5,4），最后到达（2,3），此时搜索路径中的结点为<（7,2），（5,4），（2,3）>，首先以（2,3）作为当前最近邻点，计算其到目标点（2.1,3.1）的距离为0.1414，然后回溯到其父节点（5,4），并判断在该父节点的其他子节点空间中是否有距离目标点更近的实例点。以（2.1,3.1）为圆心，以0.1414为半径画圆，如图3所示。发现该圆并不和超平面y = 4交割，因此不用进入（5,4）结点的右子空间中去搜索，因为右子空间中不可能有更近的实例点了。

图3：查找（2.1，3.1）点的两次回溯判断

于是，再回溯到结点（7,2），以目标点（2.1,3.1）为圆心，以0.1414为半径的圆更不会与超平面 x = 7 相交，因此不用进入（7,2）的右子空间进行搜索。至此，整个搜索路径为空，结束整个搜索，返回结点(2,3)作为目标点(2.1,3.1)的最近邻点，最近距离为0.141。

一个复杂点的例子如目标点为（2,4.5）。同样先进行二分查找，先从（7,2）查找到（5,4），在进行查找时是由超平面 y = 4 分割搜索空间的，由于查找点为 y 值为4.5，因此进入右子空间查找到（4,7），形成搜索路径<（7,2）,（5,4）,（4,7）>，取（4,7）为当前最近邻点，计算其与目标点的距离为3.202。然后回溯到（5,4），计算其与查找点之间的距离为3.041。以（2,4.5）为圆心，以3.041为半径作圆，如图4所示。可见该圆与超平面 y = 4 相交，所以需要进入（5,4）的左子空间进行查找。此时需将（2,3）节点加入搜索路径中得<（7,2）,（2,3）>。回溯至（2,3）叶子节点，（2,3）距离（2,4.5）比（5,4）要近，所以最近邻点更新为（2,3），最近距离更新为1.5。回溯至（7,2），以（2,4.5）为圆心1.5为半径作圆，并不和 超平面 x = 7 相交，如图5所示。至此，搜索路径回溯完毕。返回最近邻点（2,3），最近距离1.5。

图4：查找（2，4.5）点的第一次回溯判断

图5：查找（2，4.5）点的第二次回溯判断

两次搜索的返回的最近邻点虽然是一样的，但是搜索(2, 4.5)的过程要复杂一些，因为(2, 4.5)更接近超平面。研究表明，当目标点的邻域与分割超平面两侧的空间都产生交集时，需要查找另一侧子空间，回溯的次数大大增加。导致检索过程复杂，效率下降。

一般来讲，最临近搜索只需要检测几个叶子结点即可，如下图所示：

但是，如果当实例点的分布比较糟糕时，几乎要遍历所有的结点，如下所示：

研究表明 N 个节点的 k-d 树搜索过程时间复杂度最坏的情况下是 。如果实例点是随机分布的，k-d 树搜索的平均计算复杂度是 O(logN)。k-d 树更适用于训练实例 N >> 2^k 的情况，因此空间维数不能太高，一般不大于20维，当空间维数接近实例数时，它的效率会迅速下降，几乎接近贪婪线性扫描。由于大量回溯会导致 k-d 树最近邻搜索的性能大大下降，因此研究人员也提出了改进的 k-d 树近邻搜索算法，其中一个比较著名的就是 Best-Bin-First，它通过设置优先级队列和运行超时限定来获取近似的最近邻，有效地减少回溯的次数。

下面来自己实现，再看一下改进的BBF算法。