分治与递归

分治与递归

 

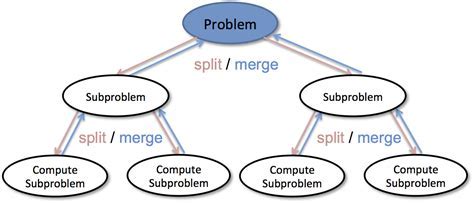
1、问题的分解

2、问题的求解

3、解的合并

 

https://bigdata.oden.utexas.edu/project/divide-conquer-methods-for-big-data-analytics/

 

普通分治：分治的各个层次的各解决方案不同；

递归分治：分治的各个层次的解决方案相同。

 

分治策略的基本思想

分治算法是 将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。如果原问题可分割成k
个子问题，1<k≤n
，且这些子问题都可解并可利用这些子问题的解求出原问题的解，那么这种分治法就是可行的。由分治法产生的子问题往往是原问题的较小模式，这就为使用递归技术提供了方便。在这种情况下，反复应用分治手段，可以使子问题与原问题类型一致而其规模却不断缩小，最终使子问题缩小到很容易直接求出其解。这自然导致递归过程的产生。

 

分治法所能解决的问题一般具有以下几个特征：

 1) 该问题的规模缩小到一定的程度就可以容易地解决

2) 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质。

3) 利用该问题分解出的子问题的解可以合并为该问题的解；

4) 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题。

第一条特征是绝大多数问题都可以满足的，因为问题的计算复杂性一般是随着问题规模的增加而增加； 

第二条特征是应用分治法的前提它也是大多数问题可以满足的，此特征反映了递归思想的应用； 

第三条特征是关键，能否利用分治法完全取决于问题是否具有第三条特征，如果具备了第一条和第二条特征，而不具备第三条特征，则可以考虑用贪心法或动态规划法。 

第四条特征涉及到分治法的效率，如果各子问题是不独立的则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然可用分治法，但一般用动态规划法较好。

————————————————

版权声明：本文为CSDN博主「松子茶」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。

原文链接：https://blog.csdn.net/songzitea/article/details/52262537

 

如果运用列表来形容归纳法就是：

步进表达式：问题蜕变成子问题的表达式

结束条件：什么时候可以不再是用步进表达式

直接求解表达式：在结束条件下能够直接计算返回值的表达式

逻辑归纳项：适用于一切非适用于结束条件的子问题的处理，当然上面的步进表达式其实就是包含在这里面了。

 

分治策略一般性描述

把上面的设计思想加以归纳,可以得到分治算法的一般描述.设P是待求解的问题,|P|代表问题的输入规模,一般的分治算法Divide-and-Conquer伪码描述如下:

算法 Divide-and-Conquer(P)

1. if |P| < c or |P| = c then S(P)

2. divide P into P1,P2,P3,...,Pk

3. for i = 1 to k do

4. yi ← Divide-and-Conquer(Pi)

5.Return Merge(y1,y2,y3,....,yk)